【CF】Day1

​​​​​​https://codeforces.com/problemset/problem/2050/B
https://codeforces.com/problemset/problem/2050/C

B. Transfusion

题目：

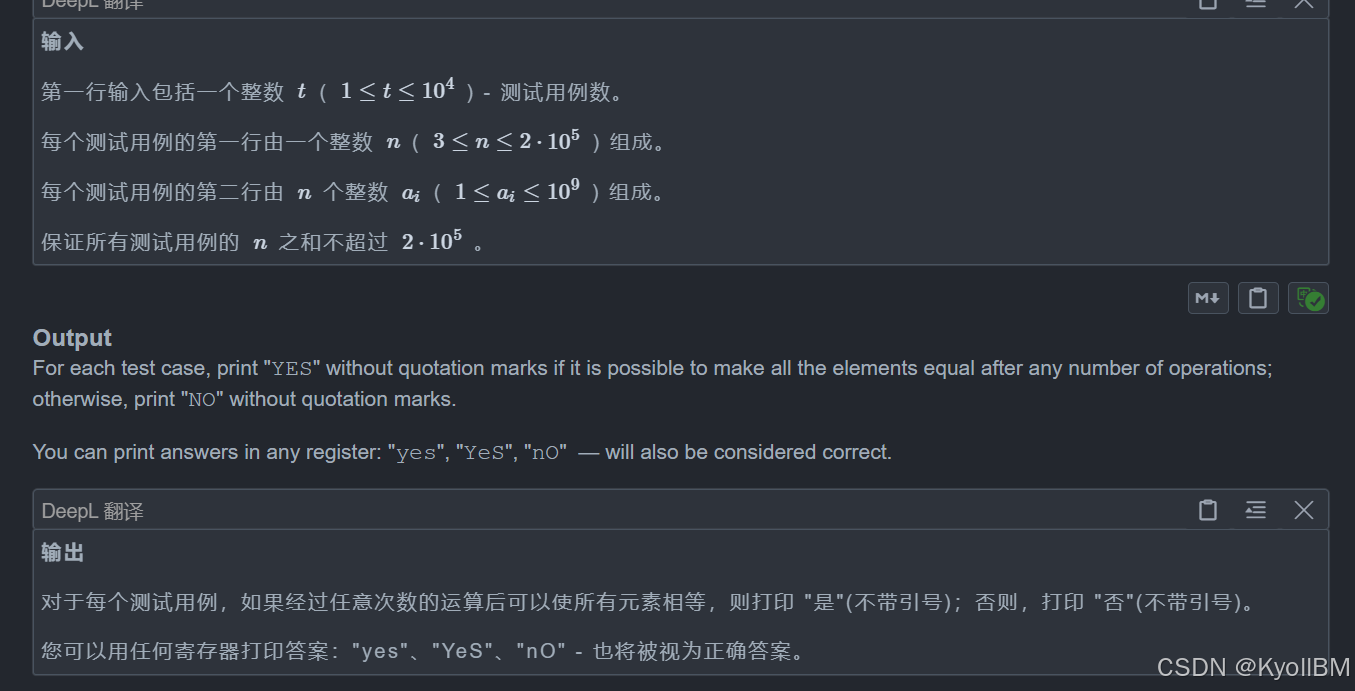
思路：

我们观察发现，每次操作都只能改变一个数左右两边的数，所以可以知道只能对奇数位or偶数位的数字进行加一减一操作

首先最后要使所有数变成同一个数，那么最后肯定有奇数位的数的和的平均数等于偶数位的和的平均数

其次每次操作都不会使得和改变，所以我们可以大胆操作，那么什么情况下不可以呢？

显然，当奇数or偶数的平均数不是整数时就肯定不行，否则必定可以使得所有数都变成平均数

证明（来自D小姐的数学归纳法）：

基例：当数组长度为1时，只有一个元素，它本身就是A，无需任何操作。

归纳假设：假设对于长度为k的数组，可以通过一系列操作将所有元素变成A。

归纳步骤：考虑长度为k+1的数组。

1. 找到第一个不等于A的元素。假设这个元素大于A（小于A的情况类似）。

2. 由于总和不变，必然存在另一个元素小于A。

3. 通过一系列相邻的加减操作，将多余的值从大于A的元素转移到小于A的元素。

4. 重复这个过程，直到所有元素都等于A。

由于每次操作都减少了至少一个元素与A的差距，且总和保持不变，最终所有元素都会变成A。

代码：

#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define ll long long
#define yes cout << "YES" << endl
#define no cout << "NO" << endl

void solve()
{
    int n;
    cin >> n;
    ll ji = 0, ou = 0;
    ll cntj = 0, cnto = 0;
    for (int i = 1; i <= n; i++)
    {
        ll x;
        cin >> x;
        if (i & 1)
            ji += x,cntj++;
        else
            ou += x,cnto++;
    }
    if ((ji % cntj == 0) && (ou % cnto == 0) && 
        (ji / cntj) == (ou / cnto))
    {
        yes;
    }
    else
    {
        no;
    }
}

int main()
{
    cin.tie(0)->sync_with_stdio(false);
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}

C. Uninteresting Number

题目：

思路：

首先我们要知道，如果一个数能被9整除，那么一定有该数每个位相加之和能被9整除，如342

那我们再看题目，由于x²一定要小于10，那么x只能取0，1，2，3，可以发现0，1对数是没有影响的，那么接下来直接考虑2，3即可，我们如果对3进行平方操作，那么对数位增加3*3-3=6，同理可以计算出2的奉献为2，那么接下来我们只需要枚举3和2是否要平方操作了

我们可以直接暴力枚举，如果增加的奉献最后对9取模刚好等于原数对9取模的值，说明肯定可以实现，因为同余有加减操作，所以直接取模是没问题的

代码：

#include <iostream>
#include <algorithm>
#include<cstring>
#include<cctype>
#include<string>
#include <set>
#include <vector>
#include <cmath>
#include <queue>
#include <unordered_set>
#include <map>
#include <unordered_map>
#include <stack>
#include <memory>
using namespace std;
#define ll long long
#define yes cout << "YES" << endl
#define no cout << "NO" << endl

void solve()
{
    string s;
    cin >> s;
    ll n = 0;
    ll has[2] = { 0,0 };
    for (int i = 0; i < s.length(); i++)
    {
        n += s[i] - '0';
        if (s[i] == '2')
        {
            has[0]++;
        }
        else if (s[i] == '3')
        {
            has[1]++;
        }
    }
    if (n % 9 == 0)
    {
        yes;
        return;
    }
    int need = 9 - n % 9;
    for (int i = 0; i <= has[0]; i++)
    {
        for (int j = 0; j <= has[1]; j++)
        {
            if ((i*2+j*6) % 9 == need)
            {
                yes;
                return;
            }
        }
    }
    no;
}

int main()
{
    cin.tie(0)->sync_with_stdio(false);
    int t = 1;
    cin >> t;
    while (t--)
    {
        solve();
    }
    return 0;
}