CVPR2018 | MI-FGSM | 利用动量增强对抗性攻击

---

论文链接

这篇文章 “Boosting Adversarial Attacks with Momentum” 主要介绍了一种基于动量迭代梯度的方法来增强对抗性攻击，提出了动量迭代快速梯度符号法（MI-FGSM），并通过实验验证了其有效性。

---

摘要-Abstract

Deep neural networks are vulnerable to adversarial examples, which poses security concerns on these algorithms due to the potentially severe consequences. Adversarial attacks serve as an important surrogate to evaluate the robustness of deep learning models before they are deployed. However, most of existing adversarial attacks can only fool a black-box model with a low success rate. To address this issue, we propose a broad class of momentum-based iterative algorithms to boost adversarial attacks. By integrating the momentum term into the iterative process for attacks, our methods can stabilize update directions and escape from poor local maxima during the iterations, resulting in more transferable adversarial examples. To further improve the success rates for black-box attacks, we apply momentum iterative algorithms to an ensemble of models, and show that the adversarially trained models with a strong defense ability are also vulnerable to our black-box attacks. We hope that the proposed methods will serve as a benchmark for evaluating the robustness of various deep models and defense methods. With this method, we won the first places in NIPS 2017 Non-targeted Adversarial Attack and Targeted Adversarial Attack competitions.

深度神经网络容易受到对抗样本的攻击，由于潜在的严重后果，这对这些算法构成了安全隐患。对抗性攻击是在深度学习模型部署之前评估其鲁棒性的重要替代方法。然而，现有的大多数对抗性攻击只能以较低的成功率欺骗黑盒模型。为了解决这个问题，我们提出了一大类基于动量的迭代算法来增强对抗性攻击。通过将动量项整合到攻击的迭代过程中，我们的方法可以稳定更新方向，并在迭代过程中逃离较差的局部最大值，从而产生更具迁移性的对抗样本。为了进一步提高黑盒攻击的成功率，我们将动量迭代算法应用于一组模型，并表明具有强大防御能力的对抗训练模型也容易受到我们的黑盒攻击。 我们希望所提出的方法将成为评估各种深度模型和防御方法鲁棒性的基准。凭借这种方法，我们在NIPS 2017非目标对抗性攻击和目标对抗性攻击竞赛中均获得了第一名。

---

引言-Introduction

该部分主要介绍了深度学习模型在对抗样本攻击下的脆弱性，以及现有攻击方法在黑盒攻击中面临的问题，进而引出本文提出的基于动量的迭代算法来解决这些问题，具体内容如下：

1. 深度神经网络的脆弱性
   • 深度神经网络易受对抗样本攻击，对抗样本通过添加微小不可察觉的噪声，使模型输出错误预测。
   • 生成对抗样本有助于在模型部署前识别其脆弱性，也可为评估模型鲁棒性提供多样训练数据。
2. 现有攻击方法及问题
   • 白盒攻击方法：包括优化法（如 box-constrained L-BFGS）、单步梯度法（如 FGSM）和迭代梯度法（如 I-FGSM），它们能在已知模型结构和参数时成功生成对抗样本。
   • 黑盒攻击问题：现有攻击方法在黑盒攻击中效果不佳，尤其是对有防御机制的模型。优化法和迭代法生成的对抗样本迁移性差，单步梯度法虽迁移性较好但白盒攻击成功率低。Papernot 等人的方法需目标模型预测置信度和大量查询，不实用。
3. 本文贡献
   • 提出动量迭代梯度法，通过累积损失函数梯度稳定优化、逃离局部最优，提高攻击成功率。
   • 研究攻击模型集成的方法，增强对抗样本迁移性，保持高攻击成功率。
   • 首次证明集成对抗训练的强防御模型也易受黑盒攻击，为评估模型和防御方法鲁棒性提供新基准。

图1. 我们展示了由 Inception v3 模型的动量迭代快速梯度符号法（MI-FGSM）生成的两个对抗样本。左栏：原始图像。
中间列：通过应用 MI-FGSM 进行 10 次迭代来对抗噪声。
右栏：生成的对抗图像。
我们还展示了 Inception v3 给出的这些图像的预测标签和概率。

---

背景-Backgrounds

该部分主要介绍了对抗攻击和防御方法的背景知识，以及相关工作的回顾，具体内容如下：

1. 对抗攻击的目标
   • 给定一个分类器 $f(x)$，对抗攻击的目标是在输入 $x$ 的附近找到一个被错误分类的对抗样本 $x^{\ast }$。
   • 对抗样本分为非目标和目标两类，非目标对抗样本使 $f(x^{\ast })\ne y$（$y$ 为真实标签），目标对抗样本使 $f(x^{\ast })=y^{\ast }$（$y^{\ast }$ 为攻击者指定的目标标签且 $y^{\ast }\ne y$），同时要求对抗噪声的 $L_p$ 范数小于允许值 $ϵ$.
2. 攻击方法分类
   • 单步梯度法：如 FGSM 通过最大化损失函数生成满足 $L_{\infty }$ 范数界的对抗样本，FGM是其推广到 $L_2$ 范数界的形式。
   • 迭代法：如I-FGSM以小步长 $\alpha$ 多次应用快速梯度方法，通过迭代更新对抗样本，但生成的对抗样本迁移性差。
   • 优化法：如 box-constrained L-BFGS 直接优化对抗样本与真实样本的距离，同时满足错误分类条件，但不能保证 $L_{\infty }(L_2)$ 距离小于要求值，且黑盒攻击效果不佳。
3. 防御方法
   • 对抗训练是增强 DNNs 鲁棒性的常用方法，通过在训练过程中注入对抗样本，使模型学习抵抗损失函数梯度方向的扰动，但不能防御黑盒攻击。
   • 集成对抗训练通过使用来自多个模型的对抗样本来扩充训练数据，增强了模型对一步攻击和黑盒攻击的鲁棒性。

---

方法-Methodology

动量迭代快速梯度符号法-Momentum iterative fast gradient sign method

该部分主要介绍了动量迭代快速梯度符号法（MI-FGSM），包括其原理、算法步骤以及与其他方法的对比，具体内容如下：

1. 原理
   • 动量方法通过累积损失函数梯度方向的速度向量来加速梯度下降算法，有助于突破峰谷、小凸起和局部最优解。在生成对抗样本时，该方法能稳定更新方向，提高对抗样本的迁移性。
   • FGSM 基于数据点周围决策边界线性假设，仅应用一次梯度符号生成对抗样本，但在实际中，当扰动较大时，线性假设可能不成立，导致生成的对抗样本“欠拟合”模型，攻击能力受限。
   • 迭代 FGSM 在每次迭代中贪婪地朝着梯度符号方向移动对抗样本，容易陷入局部最大值，导致对抗样本“过拟合”模型，迁移性差。
   • MI-FGSM 通过整合动量解决了上述问题，在增加迭代次数时保持了对抗样本的迁移性，同时增强了对白盒模型的攻击能力，缓解了攻击能力与迁移性之间的权衡。
2. 算法步骤（见Algorithm 1）
   • 输入：分类器 $f$ 及其损失函数 $J$、真实样本 $x$ 和其真实标签 $y$、扰动大小 $ϵ$、迭代次数 $T$ 和衰减因子 $\mu$.
   • 初始化：计算扰动步长 $\alpha =ϵ/T$，初始化速度向量 $g_0=0$ 和对抗样本 $x_0^{\ast }=x$.
   • 迭代过程：在每次迭代 $t$（$0$ 到 $T-1$）中，将 $x_t^{\ast }$ 输入分类器得到梯度 ${\nabla }_{x}J(x_t^{\ast },y)$，通过 $g_{t+1}=\mu \cdot g_t+\frac{{\nabla }_{x}J(x_t^{\ast },y)}{\parallel {\nabla }_{x}J(x_t^{\ast },y){\parallel }_1}$ 更新速度向量，然后根据 $x_{t+1}^{\ast }=x_t^{\ast }+\alpha \cdot sign(g_{t+1})$ 更新对抗样本。
   • 输出：返回满足 $L_{\infty }$ 范数限制的对抗样本 $x_T^{\ast }$.
3. 与其他方法对比：当 $\mu =0$ 时，MI - FGSM退化为迭代 FGSM。通过在迭代过程中累积梯度信息，MI - FGSM 在攻击能力和迁移性上优于 FGSM 和迭代 FGSM，尤其是在黑盒攻击中表现更为显著。

攻击模型集成-Attacking ensemble of models

该部分主要研究了如何有效地攻击模型集成，提出了在 $logits$ 上融合多个模型的方法，并与其他集成方法进行了比较，具体内容如下：

1. 攻击模型集成的思路
   • 集成方法在研究和竞赛中广泛用于提高性能和增强鲁棒性，该思想也可应用于对抗攻击。如果一个样本对多个模型都具有对抗性，那么它可能捕捉到了一种内在的方向，既能欺骗这些模型，又更有可能迁移到其他模型，从而实现强大的黑盒攻击（参考文章）。
2. 在 logits 上集成模型的方法（ensemble in logits）
   • 对于攻击由 $K$ 个模型组成的集成，将模型的 $logits$ 进行融合（$logits$ 是模型在进行分类任务时，最后一层线性输出的结果，它是未经过任何激活函数处理的值。也可以理解为是每个类别对应的原始得分或对数几率（log-odds）），公式为 $l(x)={\sum }_{k=1}^K{w}_k{l}_k(x)$，其中 $l_k(x)$ 是第 $k$ 个模型的 $logits$，$w_k$ 是集成权重且 ${\sum }_{k=1}^K{w}_k=1$。
   • 损失函数 $J(x,y)$ 定义为基于融合后的 $logits$ $l(x)$ 和真实标签 $y$ 的 $softmax$ 交叉熵损失，即 $J(x,y)=-1_y\cdot log(softmax(l(x)))$，其中 $1_y$ 是 $y$ 的 one-hot 编码。
   • 以这种方式融合模型的输出，能够聚合所有模型的详细信息，从而更容易发现其脆弱性，提高攻击能力。在Algorithm 2中详细描述了针对多个模型 $logits$ 平均融合的 MI-FGSM 算法步骤，包括初始化、迭代计算融合 $logits$、获取损失和梯度、更新速度向量和对抗样本，最终返回满足条件的对抗样本。
     
3. 与其他集成方法对比
   • 除了在 logits 上融合模型，还介绍了另外两种集成方案：在预测上平均（ensemble in predictions），即 $p(x)={\sum }_{k=1}^K{w}_k{p}_k(x)$，其中 $p_k(x)$ 是第 $k$ 个模型对输入 $x$ 的预测概率；在损失上平均（ensemble in loss），即 $J(x,y)={\sum }_{k=1}^K{w}_k{J}_k(x,y)$。
   • 通过实验对比发现，在各种攻击方法和集成中的不同模型情况下，在 logits 上融合的方法（ensemble in logits）在白盒和黑盒攻击中均始终优于在预测上平均和在损失上平均的方法，表现出更好的攻击能力。这表明在logits上融合模型的方案更适合用于对抗攻击。

扩展-Extensions

该部分主要介绍了动量迭代方法在其他攻击设置中的扩展，包括 $L_2$ 范数攻击和目标攻击，具体内容如下：

1. 扩展到 $L_2$ 范数攻击
   • 为了找到在 $L_2$ 距离 $ϵ$ 范围内的对抗样本（${\Vert x^{\ast }-x\Vert }_2\le ϵ$），提出了迭代快速梯度法（MI - FGM）的动量变体。
   • 其更新公式为 $x_{t+1}^{\ast }=x_t^{\ast }+\alpha \cdot \frac{g_{t+1}}{\parallel g_{t+1}{\parallel }_2}$，其中 $g_{t+1}$ 的计算方式与MI - FGSM中相同（$g_{t+1}=\mu \cdot g_t+\frac{{\nabla }_{x}J(x_t^{\ast },y)}{\parallel {\nabla }_{x}J(x_t^{\ast },y){\parallel }_1}$），$\alpha =ϵ/T$，$T$ 为总迭代次数。通过这种方式，将动量迭代方法推广到了 $L_2$ 范数攻击设置，使得在满足 $L_2$ 范数约束的条件下，能够生成有效的对抗样本。
2. 扩展到目标攻击
   • 在目标攻击中，目标是找到被错误分类为目标类 $y^{\ast }$ 的对抗样本，其目标是最小化损失函数 $J(x^{\ast },y^{\ast })$.
   • 累积梯度的计算方式为 $g_{t+1}=\mu \cdot g_t+\frac{J(x_t^{\ast },y^{\ast })}{\parallel {\nabla }_{x}J(x_t^{\ast },y^{\ast }){\parallel }_1}$.
   • 对于 $L_{\infty }$ 范数界的目标攻击，对抗样本的更新公式为 $x_{t+1}^{\ast }=x_t^{\ast }-\alpha \cdot sign(g_{t+1})$；对于 $L_2$ 范数界的目标攻击，更新公式为 $x_{t+1}^{\ast }=x_t^{\ast }-\alpha \cdot \frac{g_{t+1}}{\parallel g_{t+1}{\parallel }_2}$。通过这些扩展，动量迭代方法能够应用于目标攻击场景，提高了在目标攻击中的有效性，使得攻击者能够更精准地控制对抗样本的生成，以达到误导模型输出特定目标标签的目的。

---

实验-Experiments

设置-Setup

该部分主要介绍了实验的设置，包括所使用的模型、数据集、攻击方法以及实验的参数设置等内容，具体如下：

1. 模型选择
   • 研究了七个模型，其中四个为正常训练模型，分别是Inception v3（Inc - v3）、Inception v4（Inc - v4）、Inception Resnet v2（IncRes - v2）、Resnet v2 - 152（Res - 152）。
   • 另外三个是通过集成对抗训练得到的模型，即 Inc - v3${}_{ens3}$、Inc - v3${}_{ens4}$、IncRes - v2${}_{ens}$，并将这三个模型简称为“对抗训练模型”。
2. 数据集选择
   • 从 ILSVRC 2012 验证集中随机选取 1000 张属于 1000 个类别的图像，这些图像均能被所选模型正确分类，以确保实验中攻击成功率的评估具有意义，避免因原始图像分类错误而干扰对攻击效果的判断。
3. 攻击方法比较
   • 实验主要比较了所提出的方法与单步梯度法和迭代法。由于优化法无法明确控制对抗样本与真实样本之间的距离，所以未直接与优化法进行比较，但指出其与迭代法具有相似性质（如在黑盒攻击效果不佳方面）。
4. 实验参数设置
   • 为了清晰展示实验结果，在非目标攻击中仅报告基于 $L_{\infty }$ 范数界的实验结果，而将基于 $L_2$ 范数界和目标攻击的结果放在补充材料中。文中指出本文的发现具有普遍性，适用于不同的攻击设置。在后续实验中，如攻击单个模型和攻击模型集成的实验，均基于此实验设置进行，为整个实验提供了统一的基础框架，确保实验结果的可比性和有效性。

攻击单个模型

该部分主要报告了针对单个模型的攻击实验结果，包括不同攻击方法的成功率对比、MI-FGSM 算法中关键因素（如衰减因子、迭代次数、更新方向、扰动大小）对攻击成功率的影响分析，具体内容如下：

1. 攻击成功率对比
   • 表1展示了使用 FGSM、I-FGSM 和 MI-FGSM 三种攻击方法分别对 Inc-v3、Inc-v4、IncRes-v2 和 Res-152 四个模型生成对抗样本的攻击成功率。成功率定义为使用对抗图像作为输入时相应模型的错误分类率。
   • 实验结果表明，MI-FGSM 在白盒攻击中表现强劲，成功率接近100%，与 I-FGSM 类似。但在黑盒攻击中，I-FGSM 相较于一步 FGSM 成功率降低，而 MI-FGSM 通过整合动量显著优于 FGSM 和 I-FGSM，在大多数黑盒攻击情况下，其成功率是 I-FGSM 的两倍以上，证明了 MI-FGSM 算法的有效性。同时，也指出 MI-FGSM 在黑盒攻击对抗训练模型（如 IncRes - v2${}_{ens}$）时成功率仍较低（小于16%），后续将通过集成方法改进。

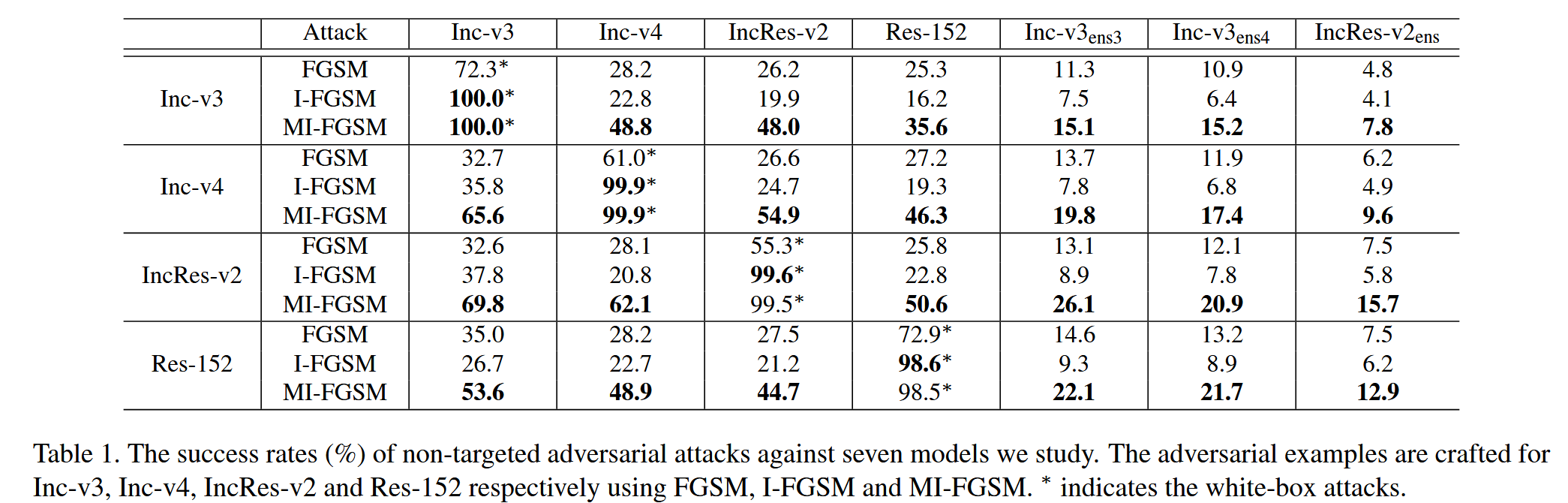
表1. 我们所研究的七种模型的非目标对抗性攻击成功率（%）。分别使用FGSM、I-FGSM 和 MI-FGSM 为 Inc - v3、Inc - v4、IncRes-v2 和 Res-152 精心制作对抗样本。$\ast$表示白盒攻击.

2. MI-FGSM 关键因素分析

• 衰减因子 $\mu$：衰减因子对提高攻击成功率起着关键作用，当 $\mu =0$ 时，动量迭代方法退化为普通迭代方法。通过对 Inc - v3 模型进行攻击实验，研究 $\mu$ 在 0.0 到 2.0 范围内（步长为0.1）时对抗样本的成功率，发现针对黑盒模型的成功率曲线呈单峰状，在 $\mu \approx 1.0$ 时达到最大值，此时 $g_t$ 可理解为简单累加所有先前梯度进行当前更新。

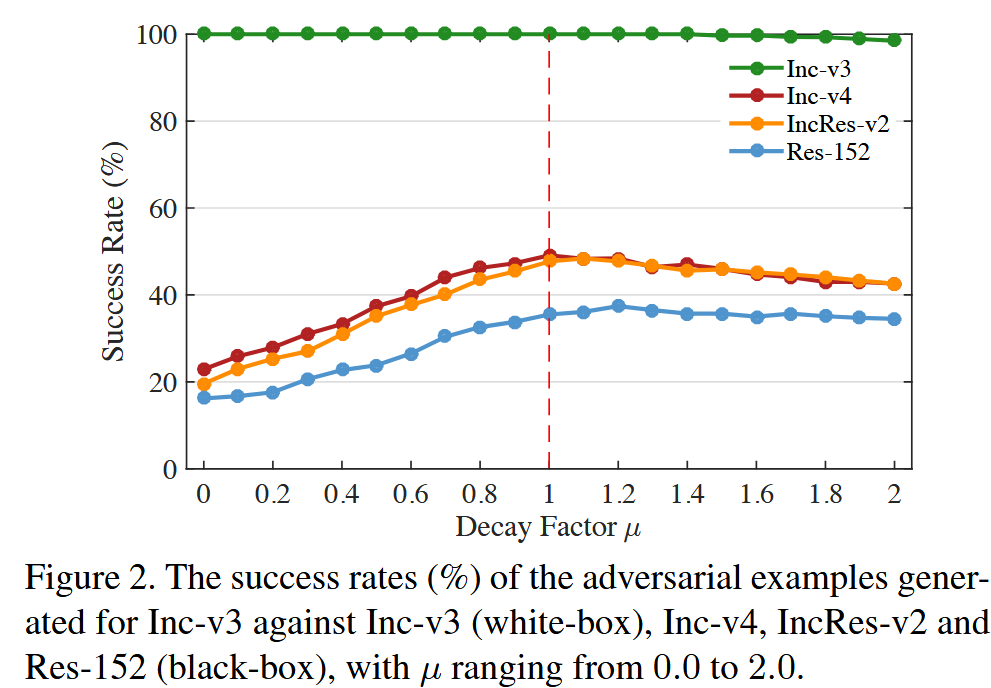
图2. 针对 Inc-v3 生成的对抗样本在攻击 Inc-v3（白盒）、Inc-v4、IncRes-v2 和 Res-152（黑盒）时的成功率（%），其中 $\mu$ 的取值范围从0.0到2.0.

• 迭代次数：采用相同超参数（$ϵ=16$，$\mu =1.0$），用 I-FGSM 和 MI-FGSM 攻击 Inc-v3模型，改变迭代次数从1到10，并评估对抗样本对其他模型（Inc-v4、IncRes-v2、Res-152）的成功率。结果显示，随着迭代次数增加，I-FGSM 对黑盒模型的成功率逐渐降低，而 MI-FGSM 仍保持较高成功率，证明了迭代方法生成的对抗样本容易过拟合白盒模型而降低迁移性，而基于动量的迭代方法能缓解这种权衡，同时对自盒和黑盒模型保持较强攻击能力。

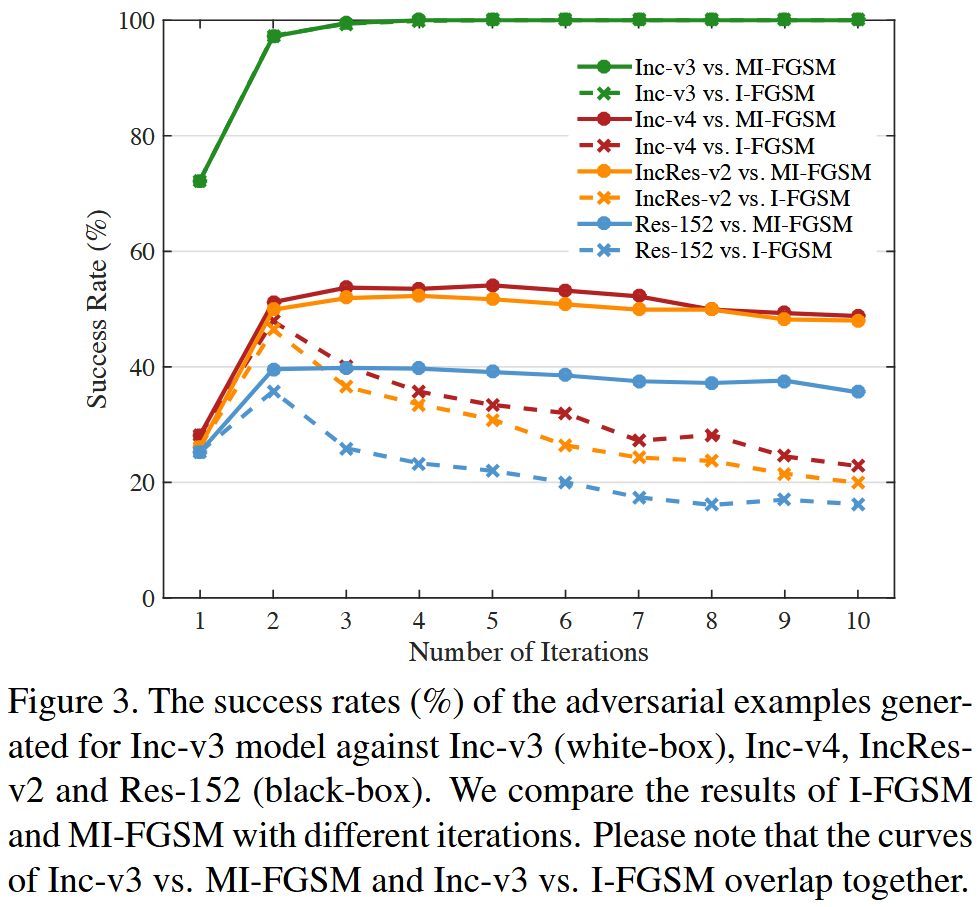
图3. 针对 Inc-v3 模型生成的对抗样本在攻击Inc - v3（白盒）、Inc-v4、IncRes-v2 和 Res-152（黑盒）时的成功率（%）。我们比较了不同迭代次数下 I-FGSM 和 MI-FGSM 的结果。请注意，Inc-v3 与 MI-FGSM 以及 Inc-v3 与 I-FGSM 的曲线重叠在一起.

• 更新方向：为解释 MI-FGSM 迁移性更好的原因，计算并比较了 I-FGSM 和 MI-FGSM 在攻击 Inc-v3 时连续两次扰动的余弦相似度。结果表明 MI-FGSM 的更新方向更稳定（余弦相似度更大），这有助于逃离模型决策边界附近的特殊区域（如“洞”），从而提高对抗样本的迁移性，因为这些特殊区域对应优化过程中的局部最大值，迭代方法易陷入其中导致迁移性差，而稳定的更新方向还可能使扰动的 $L_2$ 范数更大，进一步有助于迁移性。

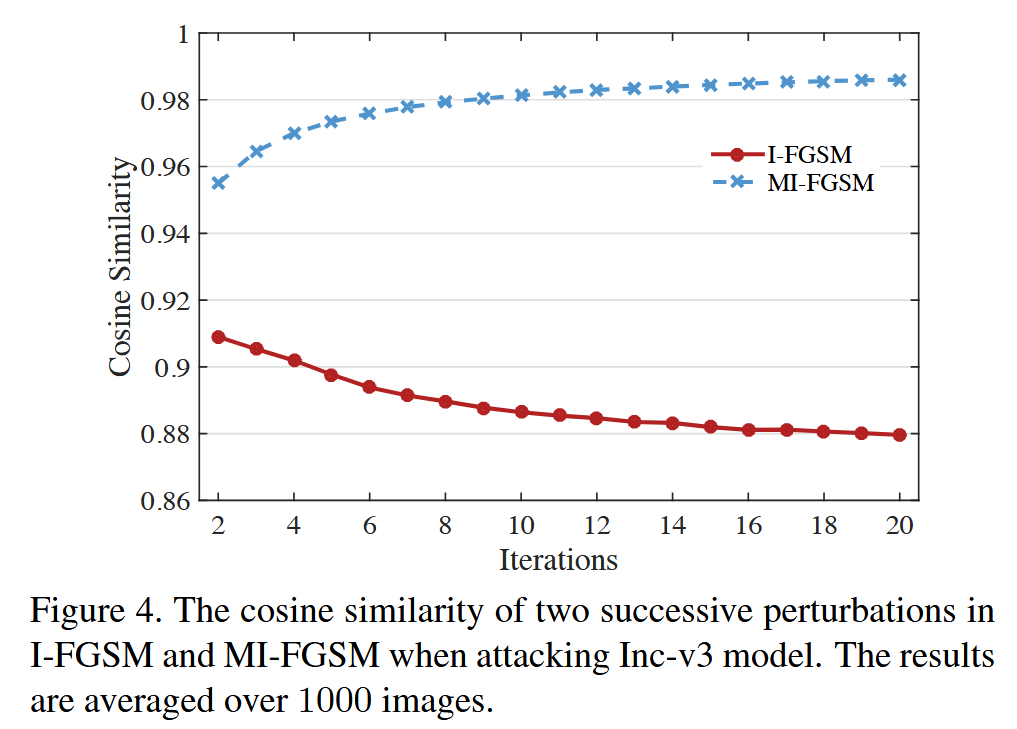
图4. 在攻击 Inc-v3 模型时，I-FGSM 和 MI-FGSM 中连续两次扰动的余弦相似度。结果是在 1000 张图像上取平均值.

• 扰动大小 $ϵ$：用 FGSM、I-FGSM 和 MI-FGSM 攻击 Inc-v3 模型，改变 $ϵ$ 从 1 到 40，在 I-FGSM 和 MI-FGSM 中设置步长 $\alpha =1$，使迭代次数随 $ϵ$ 线性增长。对于白盒攻击，迭代方法很快达到 100% 成功率，但 FGSM 在扰动较大时成功率下降，原因是大扰动时决策边界线性假设不适用；对于黑盒攻击，三种方法成功率随 $ϵ$ 线性增长，但 MI-FGSM 增长更快，意味着攻击黑盒模型达到相同成功率时，MI-FGSM 可使用更小扰动，视觉上更难被人察觉。

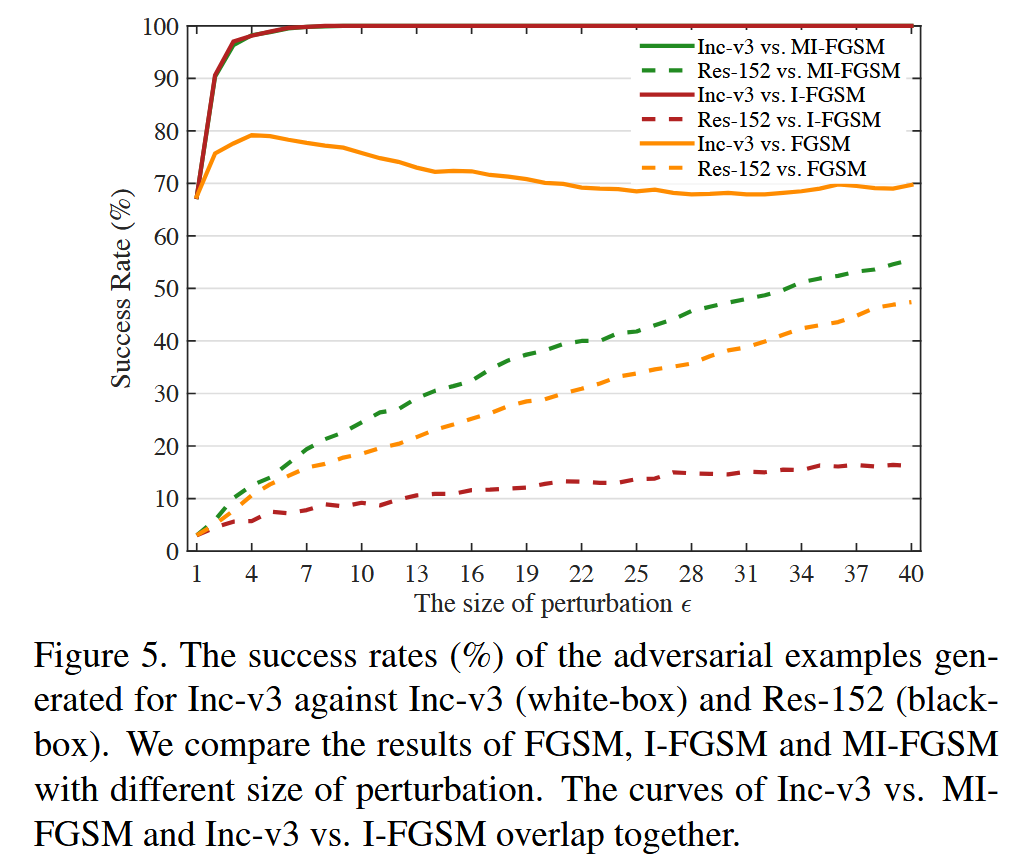
图5. 针对 Inc-v3 生成的对抗样本在攻击 Inc-v3（白盒）以及 Res-152（黑盒）时的成功率（%）。我们对比了 FGSM（快速梯度符号法）、I-FGSM（迭代快速梯度符号法）和 MI-FGSM（动量迭代快速梯度符号法）在不同扰动大小情况下的结果。Inc-v3 与 MI-FGSM 以及 Inc-v3 与 I-FGSM 的曲线重叠在一起.

攻击模型集成-Attacking an ensemble of models

该部分主要展示了攻击模型集成的实验结果，包括比较不同的集成方法以及针对对抗训练模型的攻击实验，具体内容如下：

1. 比较不同的集成方法

   • 实验比较了三种集成方法（在 logits 上集成、在预测上集成、在损失上集成）在攻击由 Inc-v3、Inc-v4、IncRes-v2 和 Res-152组成的模型集成时的效果。
   • 每次实验保留一个模型作为留出的黑盒目标模型，使用 FGSM、I-FGSM 和 MI-FGSM分别攻击其他三个模型的集成。实验设置为 $ϵ=16$，I-FGSM 和 MI-FGSM的迭代次数为10，MI-FGSM 的衰减因子 $\mu =1.0$，集成权重均等。
   • 结果表明，在 logits 上集成的方法在白盒和黑盒攻击中，对于所有攻击方法和集成中的不同模型，均一致优于在预测和损失上集成的方法。这表明在 logits 上融合模型的方案更适合用于对抗攻击，能够更有效地提高攻击能力。
     
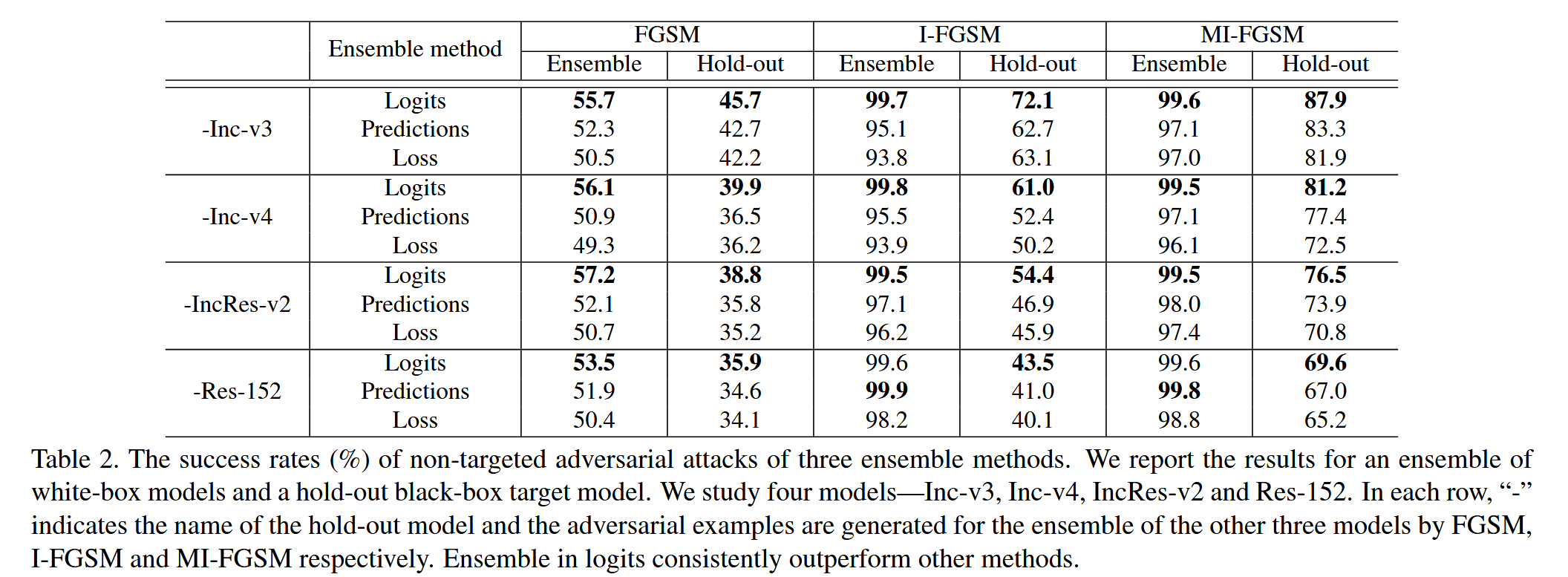
     表2. 三种集成方法的非目标对抗性攻击成功率（%）。我们展示了针对一组白盒模型以及一个留出的黑盒目标模型的实验结果。我们研究了四个模型——Inception v3（Inc-v3）、Inception v4（Inc-v4）、Inception Resnet v2（IncRes-v2）以及Resnet v2-152（Res-152）。在每一行中，“-” 表示留出模型的名称（即不包括这个模型），并且对抗样本是分别通过 FGSM（快速梯度符号法）、I-FGSM（迭代快速梯度符号法）以及 MI-FGSM（动量迭代快速梯度符号法）针对其余三个模型的集成来生成的。在logits上进行集成的方法始终优于其他方法.

2. 攻击对抗训练模型

   • 为了在黑盒方式下攻击对抗训练模型，实验纳入了实验设置部分介绍的所有七个模型。
   • 每次实验保留一个对抗训练模型作为留出的目标模型，攻击其余六个模型的集成（在 logits 上融合，集成权重均等）。设置扰动 $ϵ=16$，衰减因子 $\mu =1.0$，比较FGSM、I-FGSM 和 MI-FGSM 在 20 次迭代下的攻击结果。
   • 实验发现，对抗训练模型也不能有效防御这些攻击，例如，超过 40% 的对抗样本可以成功欺骗 Inc-v3${}_{ens4}$。这表明通过集成对抗训练得到的模型，尽管在 ImageNet 上被认为是最鲁棒的模型之一，但仍然容易受到本文提出的黑盒攻击方法的影响，从而为开发更鲁棒的深度学习模型算法带来了新的安全问题。

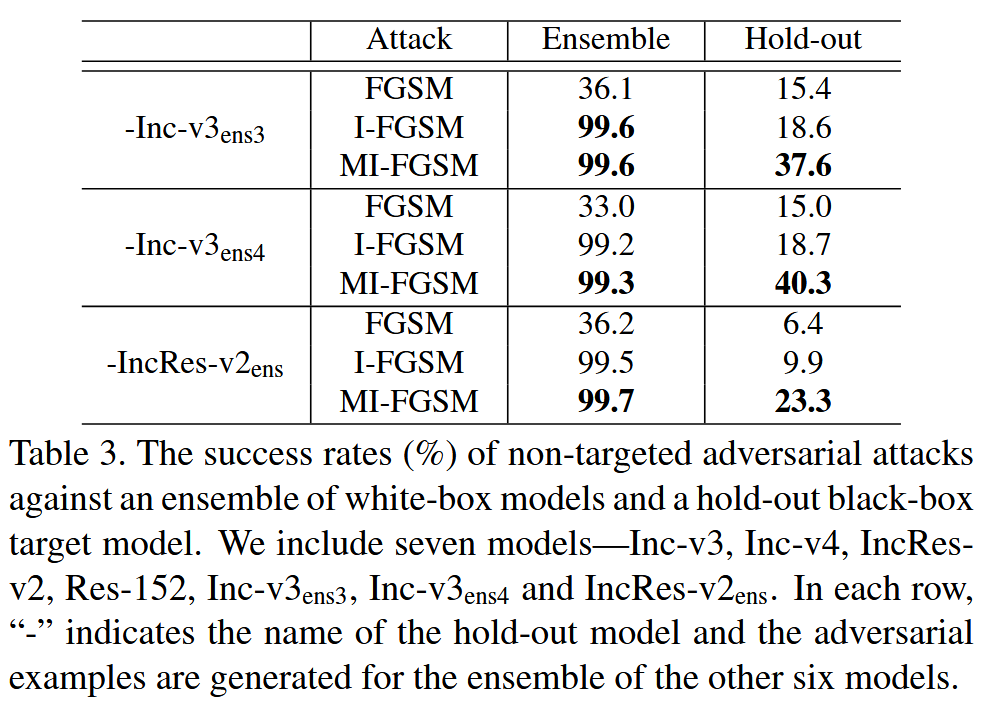
表3. 针对一组白盒模型与一个留出的黑盒目标模型的非目标对抗性攻击成功率（%）。我们纳入了七个模型——Inception v3（Inc-v3）、Inception v4（Inc-v4）、Inception Resnet v2（IncRes-v2）、Resnet v2-152（Res-152）、Inc-v3${}_{ens3}$、Inc-v3${}_{ens4}$ 以及 IncRes-v2${}_{ens}$。在每一行中，“-”表示留出模型的名称，并且对抗样本是针对其余六个模型的集成而生成的。

竞赛-Competitions

该部分部分主要介绍了在 NIPS 2017 对抗攻击竞赛中的参赛情况，包括竞赛的设置以及使用本文方法在非目标攻击和目标攻击中的具体配置及取得的成绩，具体内容如下：

1. 竞赛设置
   • NIPS 2017 对抗攻击和防御竞赛包含三个子竞赛，即非目标对抗攻击、目标对抗攻击和防御对抗攻击。
   • 组织者提供了 5000 张 ImageNet 兼容图像用于评估攻击和防御提交。对于每次攻击，为每张图像生成一个对抗样本，扰动大小范围从 4 到 16（由组织者指定），所有对抗样本将在所有防御提交中运行以获得最终分数。
2. 非目标攻击配置及成绩
   • 在非目标攻击中，实现了 MI-FGSM 来攻击由 Inc-v3、Inc-v4、IncRes-v2、Res-152、Inc - v3${}_{ens3}$、Inc - v3${}_{ens4}$、IncRes-v2${}_{ens}$ 和 Inc - v3${}_{adv}$组成的模型集成。
   • 采用在 logits 上集成的方案，前七个模型的集成权重设置为 $1/7$ 均等，Inc-v3${}_{adv}$ 的权重设置为 $0.25/7.25$。迭代次数为10，衰减因子 $\mu =1.0$。最终凭借此方法在非目标攻击竞赛中获得第一名。
3. 目标攻击配置及成绩
   • 在目标攻击中，构建了两个攻击图。当扰动大小小于8时，攻击 Inc-v3 和 IncRes-v2${}_{ens}$，集成权重分别为 $1/3$ 和 $2/3$；当扰动大小大于等于8时，攻击由 Inc-v3、Inc-v3${}_{ens3}$、Inc-v3${}_{ens4}$、IncRes-v2${}_{ens}$ 和 Inc-v3${}_{adv}$ 组成的模型集成，集成权重分别为 $4/11$、$1/11$、$1/11$、$4/11$ 和 $1/11$。
   • 迭代次数分别为40（扰动小于8时）和20（扰动大于等于8时），衰减因子 $\mu =1.0$。通过此方法在目标攻击竞赛中也获得了第一名。

---

讨论-Discussion

该部分从不同视角对对抗样本相关问题进行了讨论，将寻找对抗样本类比为训练模型，阐述了动量和集成方法提高对抗样本迁移性的合理性，具体内容如下：

1. 类比关系阐述
   • 文中提出寻找对抗样本可类比为训练模型，对抗样本的迁移性类似于模型的泛化性。在这种类比下，给定一组模型作为“训练数据”来“训练”对抗样本。
2. 方法合理性解释
   • 动量方法和集成方法能提高对抗样本的迁移性，这与在模型训练中采用动量优化器或使用更多数据可提高模型泛化性的原理相似。因此，从这个元视角来看，这些方法在对抗攻击中提高迁移性是合理的。
3. 未来研究方向展望
   • 基于上述类比，作者认为其他用于增强模型泛化性的技巧（如随机梯度下降，SGD）也可融入对抗攻击方法中，以进一步提高对抗样本的迁移性，为后续对抗攻击研究提供了新的思路和潜在研究方向。这一讨论有助于从新的角度理解对抗攻击中的相关现象，并为进一步改进攻击方法提供了理论依据。

---

结论-Conclusion

该部分主要对全文进行了总结，强调了所提出方法的贡献、有效性以及对深度学习模型安全性研究的影响，具体内容如下：

1. 研究成果总结
   • 提出了一类基于动量的迭代方法来增强对抗性攻击，该方法在白盒和黑盒攻击中均表现出色，始终优于单步梯度法和普通迭代法，有效解决了现有攻击方法在黑盒攻击中成功率低的问题。
   • 通过实验充分验证了所提方法的有效性，并深入解释了其在实际应用中发挥作用的原因，包括动量迭代如何稳定更新方向、提高对抗样本迁移性等方面。
2. 模型集成攻击的意义
   • 提出攻击模型集成的方法，特别是在logits上融合模型的方式，显著提高了对抗样本的迁移性，进一步增强了攻击能力。
3. 对模型安全性的影响
   • 研究发现即使是通过集成对抗训练获得的具有强大防御能力的模型，在黑盒攻击下仍然存在漏洞，容易受到本文方法的攻击。这一结果引发了对开发更鲁棒深度学习模型的新安全问题的关注，强调了在模型安全性研究方面仍面临挑战，需要进一步深入探索和改进防御机制，以应对不断发展的对抗攻击手段。