大致题意 : 一个n个点m条边的无重边无自环的有向图, 初始均为白点, 若某个点的前驱节点均为黑点, 则该点可以被染黑, 初始可任意染黑一点, 求最大化图中黑点的数量
思路 : 首先可以画一张图, 如样例, 起始我们染黑1, 后续2, 3可被染黑, 不难发现, 1,2,3可以互相影响, 染黑3 不如 染黑2, 染黑2 不如 染黑 1, 这时我们可以将这三个点看做一个点, 即进行合并, 可以发现合并后并不会对原图产生影响, 如节点 5 在合并和 由{1, 2, 3} 和 {4} 控制并不能染黑, 若有另一点能到{1, 2, 3}, 则{1, 2, 3}并不能合并, 可知合并后的{1, 2, 3}的前后节点不受影响, 即当前合并后的节点集合的节点数即为最大, 若有多个集合取极大值即可
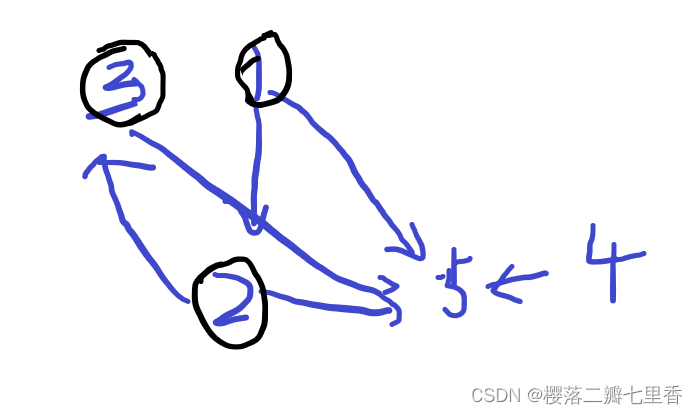
显然暴力是会超时的, 因为会遍历到所有重边来进行合并, 这里可以想到用启发式合并来进行操作, 对于两个可以连接的集合, 我们只遍历出边数小的那个集合, 将它与出边大的合并, 来优化时间复杂度, 最坏情况下m条边, 分为m/2, m/2两个集合, 每次只遍历一个, 不断向下合并, 复杂度为 O(m/2 * log m), 再加上需要用到set操作, 总时间复杂度为O(m/2 * log m * log m), 是可以做的
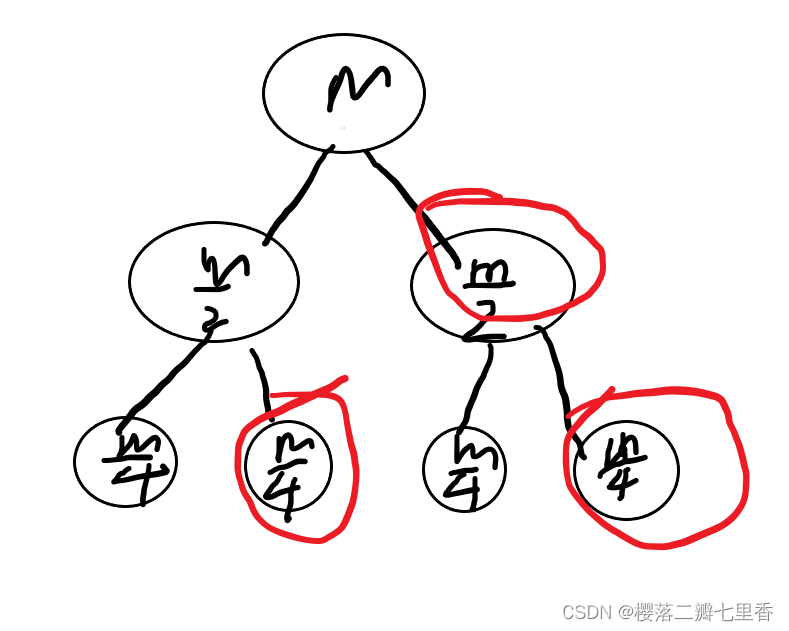





 这篇博客介绍了如何解决一个无重边无自环有向图的问题,目标是最大化黑点数量。通过启发式合并策略优化了时间复杂度,达到O(m/2*logm*logm),并提供了相应的C++代码实现。
这篇博客介绍了如何解决一个无重边无自环有向图的问题,目标是最大化黑点数量。通过启发式合并策略优化了时间复杂度,达到O(m/2*logm*logm),并提供了相应的C++代码实现。
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章


















 292
292

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








