G. 积木画(dp + 滚动数组)

原创已于 2022-05-13 15:16:37 修改 · 376 阅读

1 ·

CC 4.0 BY-SA版权

文章标签：

#动态规划 #算法

于 2022-05-13 15:11:26 首次发布

第十三届蓝桥杯B组补题专栏收录该内容

1 篇文章

订阅专栏

该博客介绍了如何使用线性动态规划(DP)解决一个关于在2*N的画布上用两种积木填满画布的问题。博主通过状态转移方程分析了三种不同的填充情况，并展示了如何通过滚动数组优化空间复杂度，从而在O(n)的时间复杂度内求解。最后给出了AC代码实现。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

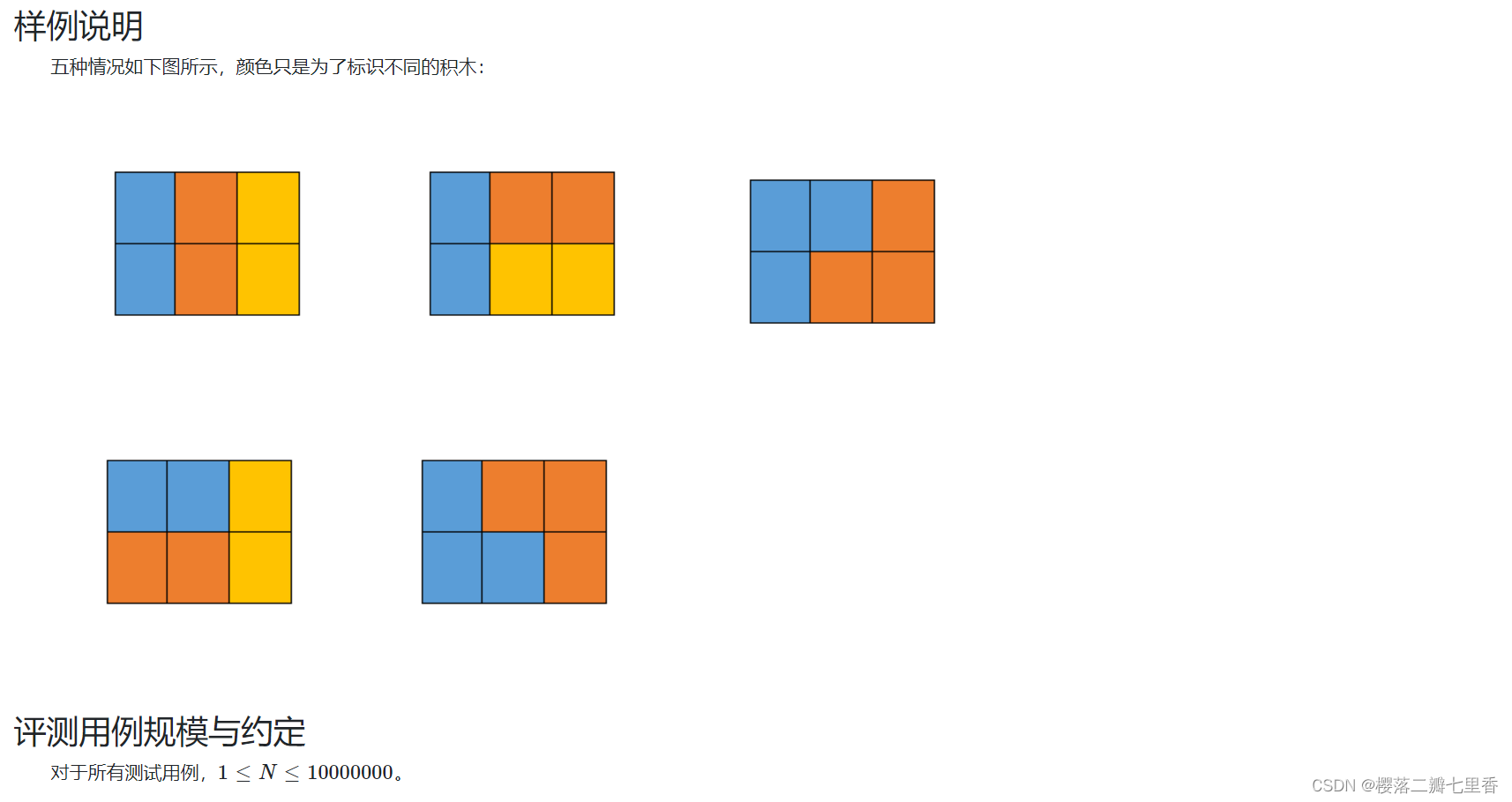
大致题意 : 给定2*N的画布, 以及两种积木, 问填满画布的方法有多少种

思路: 数据范围很大, 时间复杂度要求O(n), 可以想到用线性dp来解决

考虑状态转移方程:

状态表示: d[i][j]表示前 i 列都填满, 填满第 i+1 列时状态为j的种类数

按j分为以下三种

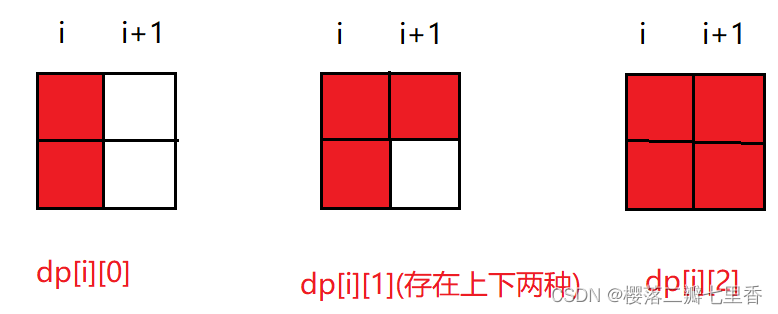
状态转移方程: 即看填满上一列的方法

第一种 : dp[i][0] = dp[i-1][0](由dp[i-1][0]加一个竖条转移过来)+ dp[i-1][2](由dp[i-1][2]什么都不加转移)

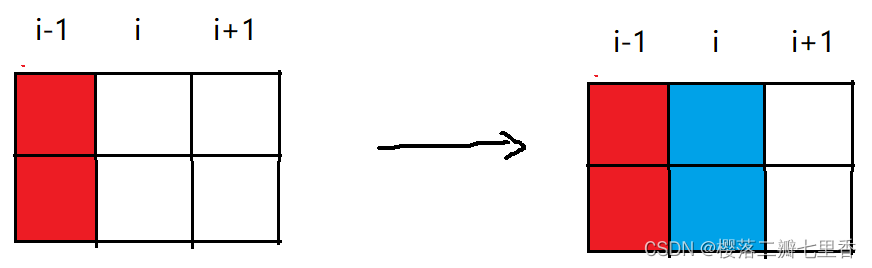
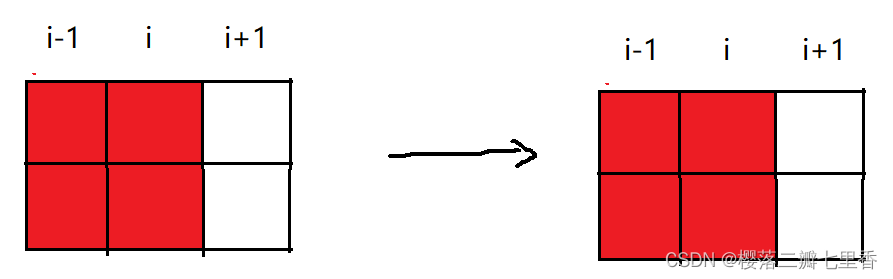
第二种: dp[i][1] = dp[i-1][0]*2(由dp[i-1][0]加一个L方块转移过来, 分为上下两种) + dp[i-1][1](由dp[i-1][0]加一个横条转移)

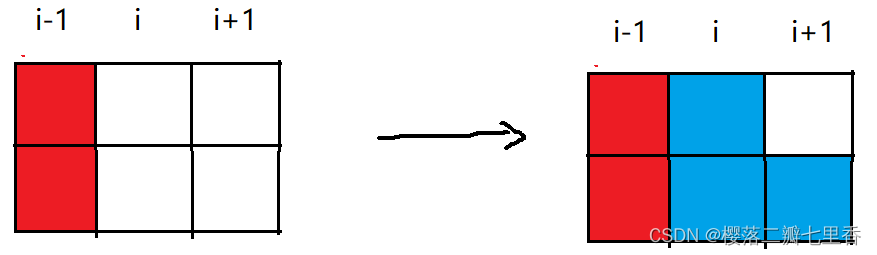
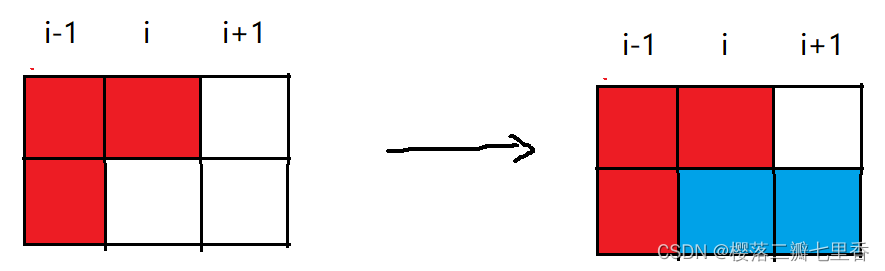
第三种: dp[i][2] = dp[i-1][0] + dp[i-1][1](这里不乘二, 因为在更新dp[i-2][1]时乘了2, 即i-2的第二种)

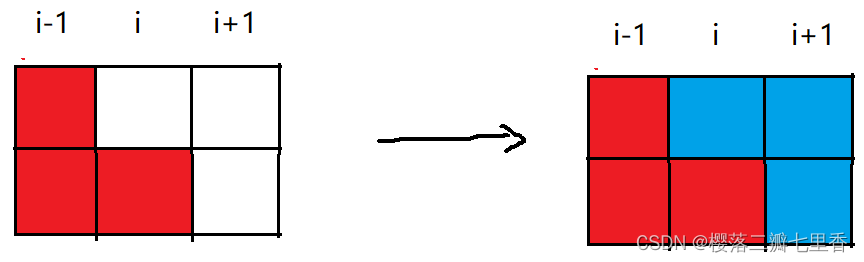
因为状态转移时i 只于 i-1有关, 所以可以通过滚动数组进行优化

dp[i&1][0] = d[i-1&1][0] + dp[i-1&1][2]
dp[i&1][1] = d[i-1&1][0]*2 + dp[i-1&1][1]
dp[i&1][2] = d[i-1&1][0] + dp[i-1&1][1]

这样开数组时可以只用开dp[2][3]而不是dp[N][3](因为N大了可能会爆内存)

最终答案即为dp[n-1&1][0], 即第n列状态为0, 前n-1列全部填满的种类数

AC代码如下:

#include <iostream>
#include <cstring>
#include <cstdio>
#include <string>
#include <iterator>
#include <cmath>
#include <algorithm>
#include <sstream>
#include <map>
#include <stack>
#include <set>
#include <queue>
#include <iomanip>
using namespace std;

stringstream ss;
typedef long long ll;
typedef pair<int, int> PII;
const int N = 25010, M = 150010, mod = 1000000007;
const int INF = 0x3f3f3f3f;

int n;
ll dp[2][3]; // dp[i][j]表示前i列填满, 填充第i+1列的状态是j的种类数

int main()
{
    ios::sync_with_stdio(false),cin.tie(0),cout.tie(0);
    cin>>n;
    // 初始化: dp[0][0], 表示前0列已经填满, 填充第1列, 状态为0
    dp[0][0] = 1;
    dp[0][1] = 2;
    dp[0][2] = 1;
    for(int i = 1; i<n; i++)
    {
        dp[i&1][0] = (dp[i-1&1][0] + dp[i-1&1][2]) % mod;
        dp[i&1][1] = (dp[i-1&1][1] + 2*dp[i-1&1][0]) % mod;
        dp[i&1][2] = (dp[i-1&1][0] + dp[i-1&1][1]) % mod;
    }
    
    cout<<dp[n-1&1][0];
}