《基本控制结构》-小组作业 (1~10）

⒈36人一次搬36块砖，男搬4，女搬2，两个小孩抬一块。要一 次搬完。问：男、女、小孩要多少？

#include <bits/stdc++.h>

using namespace std;

#define PEAPLE 36
#define BLOCKS 36

int main (void)
{
    int male;
    int female;
    int kids;

    for (male = 0; male < PEAPLE; male ++)
    {
        for (female = 0; female < PEAPLE; female ++)
        {
            for (kids = 0; kids < PEAPLE; kids ++)
            {
                if ((male + female + kids == PEAPLE) && (male * female * kids != 0) &&
                    (male * 4 + female * 2 + kids / 2 == BLOCKS) && (kids % 2 == 0))
                {
                    cout << "We need male: " << male << endl;
                    cout << "We need female: " << female << endl;
                    cout << "We need kids: " << kids << endl;
                }
            }
        }
    }

    system ("pause");
    return 0;
}

 ⒉ 找出1000以内的完数，所谓完数是指该数的各因子之和等于 该数，如6=1+2+3。

#include <iostream>

using namespace std;

int factorSum (int n);

int main (void)
{
    for (int i = 1; i < 1000; i ++)
    {
        if (i == factorSum(i))
        {
            cout << "The Wan-Number is: " << i << endl;
        }
    }

    system ("pause");
    return 0;
}

int
factorSum (int n)
{
    int sum = 1;

    for (int i = 2; i < n; i ++)
    {
        if (n % i == 0)
        {
            sum += i;
        }
    }

    return sum;
}

⒊验证6到200以内的数，符合哥德巴赫猜想（一个大于6的偶 数，可以分解成两个质数之和）。 

#include <iostream>
#include <vector>
#include <cstdbool>

using namespace std;

bool isPrime (int n);

int main (void)
{
    vector <int> prime;
    vector <int> even;

    for (int i = 6; i < 201; i ++)
    {
        if (isPrime (i) == true)
        {
            prime.push_back (i);
        }

        if (i % 2 == 0)
        {
            even.push_back (i);
        }
    }


    for (vector <int>::iterator i = even.begin (); i != even.end (); i ++)
    {
        for (vector <int>::iterator j = prime.begin (); j != prime.end (); j ++)
        {
            for (vector <int>::iterator k = prime.begin (); k != prime.end (); k ++)
            {
                if ((even[*i] == prime[*j] + prime[*k]) && (even[*i] * prime[*j] * prime[*k]) != 0)
                {
                    cout << "The even number " << even[*i] << " is " << prime[*j] << " + " << prime[*k] << endl;
                }
            }
        }
    }

    system ("pause");
    return 0;
}

bool
isPrime (int n)
{
    for (int i = 2; i * i <= n; i ++)
    {
        if (n % i == 0)
        {
            return false;
        }
    }

    return true;
}

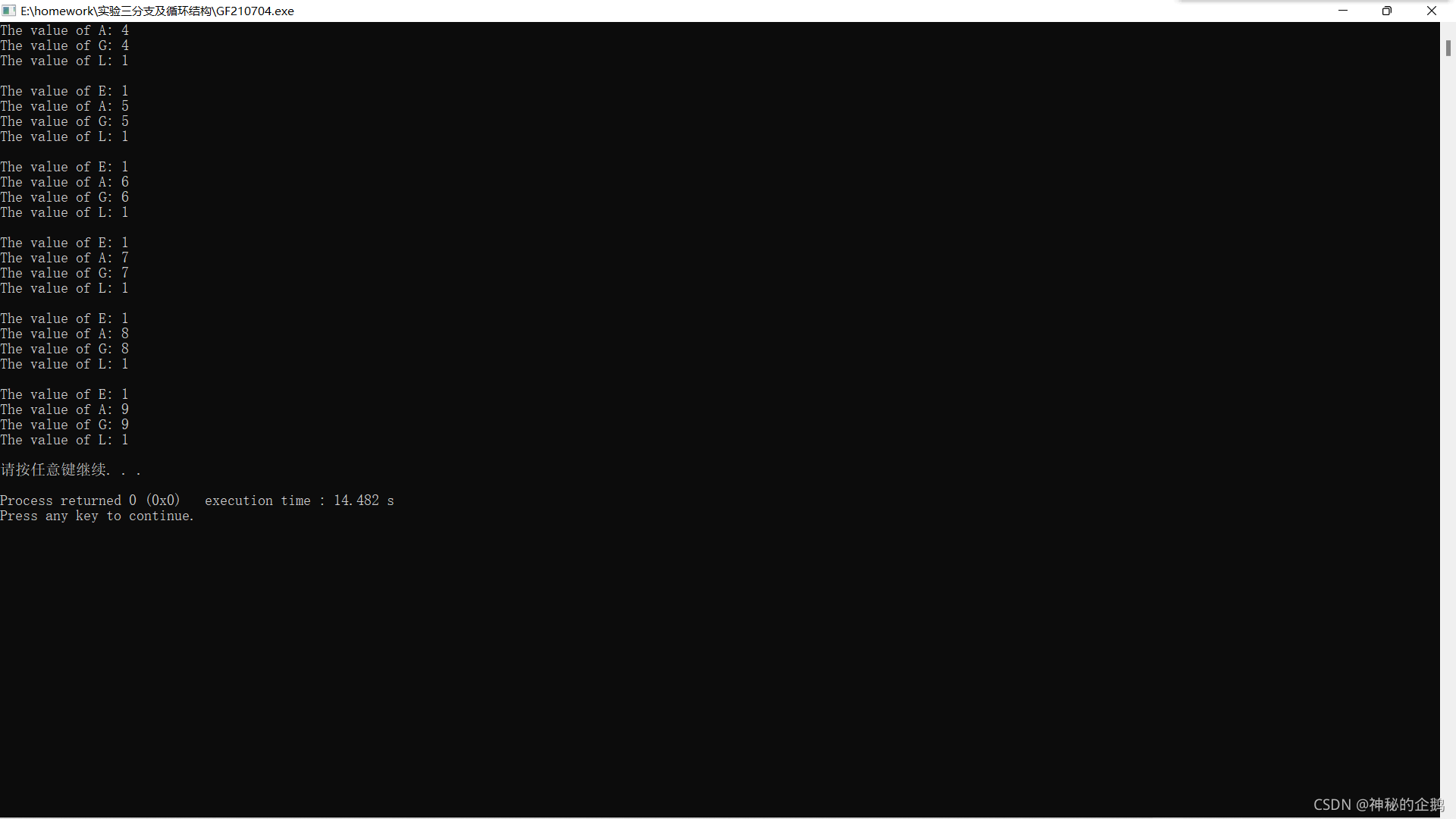
 ⒋奇妙的算式：用字母代替十进制数字写出如下算式

 E A G L x  L = L G A E 

请找出这些字母代表的数字。

#include <iostream>
#include <windows.h>

using namespace std;

int main (void)
{
    int E, A, G, L;

    for (E = 1; E < 10; E ++)
    {
        for (A = 0; A < 10; A ++)
        {
            for (G = 0; G < 10; G ++)
            {
                for (L = 1; L < 10; L ++)
                {
                    int ans = E * 1000 + A * 100 + G * 10 + L;

                    ans = ans * L;

                    if ((ans / 1000 == L) && (ans / 100 % 10 == G) &&
                        (ans / 10 % 10 == A) && (ans % 10 == E))
                    {
                        cout << "The value of E: " << E << endl;
                        cout << "The value of A: " << A << endl;
                        cout << "The value of G: " << G << endl;
                        cout << "The value of L: " << L << endl;
                        cout << '\n';

                        Sleep (1000);
                    }
                }
            }
        }
    }

    system ("pause");
    return 0;
}

⒌求自然数m和n的最大公约数。

#include <iostream>

using namespace std;

int GCD (int m, int n);

int main (void)
{
    int m, n;
    cout << "Please input two digits: ";
    cin >> m >> n;

    int gcd = GCD (m, n);
    printf ("The number %d and %d greatest common divisor(gcd) is %d \n", m, n, gcd);

    system ("pause");
    return 0;
}

int
GCD (int m, int n)
{
    if (n > m)
    {
        m = m ^ n;
        n = m ^ n;
        m = m ^ n;
    }

    int k = 0;

    while (n != 0)
    {
        k = m % n;
        m = n;
        n = k;
    }

    return m;
}

 

 ⒍用迭代法求cosX，禁止使用任何数学函数。

#include <iostream>
#include <iomanip>

using namespace std;

#define EPS 1.0e-15

double myAbs (double num);
double myCos (double x);

int main (void)
{
    double x;
    cout << "Please input a number: ";
    cin >> x;

    cout << "The value of cos(x) is: " << myCos (x) <<endl;

    system ("pause");
    return 0;
}

double
myAbs (double num)
{
    return num > 0 ? num : -num;
}

double
myCos (double x)
{
    double i = 0.0;
    int sign = 1;
    double index = 1.0;
    double Factorial = 1.0;
    double sum = 0.0;
    double TaylorExpansion  = 1.0;

    do
    {
        Factorial = Factorial * (i + 1.0) * (i + 2.0);
        index *= x * x;
        sign = ~sign + 1;
        sum = index / Factorial * (double)sign;
        TaylorExpansion += sum;
        i += 2;
    }
    while (myAbs (sum) > EPS);

    return TaylorExpansion;
}

⒎求Fibonacci级数的前40项       1，1，2，3，5，8，13，21，34….

#include <iostream>
#include <cstdio>

using namespace std;

int Fibonacci (int n);

int main (void)
{
    for (int i = 1; i <= 40; i ++)
    {
        printf ("The %2d Fibonacci is %d \n", i, Fibonacci (i));
    }

    system ("pause");
    return 0;
}

int
Fibonacci (int n)
{
    if (n < 2)
    {
        return n;
    }

    int p = 0, q = 0, r = 1;

    for (int i = 1; i < n; i ++)
    {
        p = q;
        q = r;
        r = p + q;
    }

    return r;
}

 

⒏用牛顿迭代法求方程f(x)=0的根（方法自查，方程自己构 造，要求非一次方程）。

#include <cmath>
#include <cstdio>
#include <cstdlib>
#include <iostream>

using namespace std;

#define MAX 200
#define EPS 1.0e-6

double Newton_method(double (*fun)(double a), double (*partialfun)(double b), double x);
double fun(double x);
double partialfun(double x);

int main (void)
{
    double x0;
    cout << "The function is f(x) = cos(x) + x" << endl;
    cout << "Please input the initial approximation: ";
    cin >> x0;

    double root = Newton_method (fun, partialfun, x0);

    cout << "The root of function: " << root << endl;

    system ("pause");
    return 0;
}

double
fun (double x)          //原函数
{
    return cos(x) + x;
}

double
partialfun (double x)   //原函数的导数
{
    return -sin(x) + 1;
}

double
Newton_method (double (*fun)(double), double (*partialfun)(double), double xn)
{
    double xn1;
    for (int i = 0; i < MAX; i ++)
    {
        xn1 = xn - (*fun)(xn) / (*partialfun)(xn);

        if (fabs (xn1 - xn) < EPS)
        {
            cout << "Number of Iterations: " << i + 1 << endl;

            return xn1;
        }

        xn = xn1;
    }

    cout << "The iteration divergence! " << endl;

    return NULL;
}

⒐通过梯形法求y = x^2 + 3x + 2dx 输出结果。

#include <iostream>

using namespace std;

#define N 50

double Definite_integral (double a, double b, double (*fun)(double));
double fun (double x);

int main (void)
{
    cout << "The function f(x) = x * x + 2x + 3 " << endl;
    cout << "The area for [0, 1] is: " << Definite_integral (0, 1, fun) << endl;

    system ("pause");
    return 0;
}

double
Definite_integral (double a, double b, double (*fun)(double))
{
	double x = a;
	double delta = (b - a) / N;
	double y1 = (*fun)(x), y2 = 0.0;

	double f = 0.0;
	for(int i = 0; i < N; i ++)
    {
		x += delta;
		y2 = (*fun)(x);
		f += (y1 + y2) * delta / 2.0;
		y1 = y2;
	}
	return f;
}

double
fun (double x)
{
    double f = x * x + 2.0 * x + 3.0;

    return f;
}

⒑求1000以内能被73或127整除的自然数平方根之和

#include <iostream>
#include <cmath>
#include <vector>

using namespace std;

#define N 20

int main (void)
{
    int sum1;
    int sum2;
    double ans = 0.0;

    for (int i = 1; i < N; i ++)
    {
        sum1 = i * 73;

        if (sum1 > 1000)
        {
            break;
        }

        ans += sqrt (sum1);
    }

    for (int i = 1; i < N; i ++)
    {
        sum2 = i * 127;

        if (sum2 > 1000)
        {
            break;
        }

        ans += sqrt (sum2);
    }

    cout << "The sum of numer is: " << ans << endl;

    system ("pause");
    return 0;
}