学习链接:https://www.bilibili.com/video/BV1HN4y1K7Rx?p=1&vd_source=6f1075d4365d16741b423bc01a0d8cd7
1、反转链表
给你单链表的头节点 head ,请你反转链表,并返回反转后的链表。
输入: 1->2->3->4->5
输出: 5->4->3->2->1
使用两种方式解题
1. 解法1:迭代
迭代,重复某一过程,每一次处理结果作为下一次处理的初始值,这些初始值类似于状态、每次处理都会改变状态、直至到达最终状态。
思路
从前往后遍历链表,将当前节点的next指向上一个节点,因此需要一个变量存储上一个节点prev,当前节点处理完需要寻找下一个节点,因此需要一个变量保存当前节点curr,处理完后要将当前节点赋值给prev,并将next指针赋值给curr,因此需要一共变量提前保存下一个节点的指针next
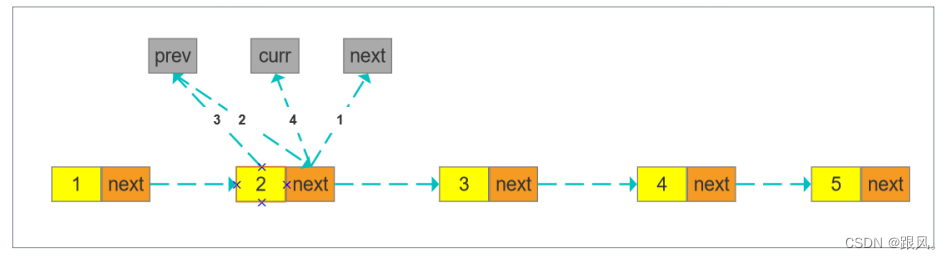
1、将下一个节点指针保存到next变量 next = curr.next
2、将下一个节点的指针指向prev,curr.next = prev
3、准备处理下一个节点,将curr赋值给prev
4、将下一个节点赋值为curr,处理一个节点
class Solution {
public ListNode reverseList(ListNode head) {
// 迭代
// 保存原前驱结点
ListNode prev = null;
// 保存原后继结点
ListNode next;
// 当前结点
ListNode cur = head;
while(cur!=null){
next = cur.next;
cur.next = prev;
prev = cur;
cur = next;
}
return prev;
}
}
- 时间复杂度:O(N)
- 空间复杂度:O(1)
2. 解法2:递归
递归:以相似的方法重复,类似于树结构,先从根节点找到叶子节点,从叶子节点开始遍历大的问题(整个链表反转)拆成性质相同的小问题(两个元素反转)curr.next.next = curr
将所有的小问题解决,大问题即解决

只需每个元素都执行curr.next.next = curr ,curr.next = null 两个步骤即可
为了保证链不断,必须从最后一个元素开始
class Solution {
public ListNode reverseList(ListNode head) {
// 递归
if(head == null || head.next==null){
return head;
}
// 递归到最后一个结点
ListNode newHead = reverseList(head.next);
head.next.next = head;
head.next=null;
return newHead;
}
}
- 时间复杂度:O(N)
- 空间复杂度:O(N)
2、寻找数组的中心下标
数组中某一个下标,左右两边的元素之后相等,该下标即为中心索引
输入:nums = [1, 7, 3, 6, 5, 6]
输出:3
1. 解法1:双指针
思路
先统计出整个数组的总和,然后从第一个元素开始叠加,总和递减当前元素,叠加递增当前元素,直到两个值相等。
class Solution {
public int pivotIndex(int[] nums) {
// 双指针
// 获取数组总和
int total = Arrays.stream(nums).sum();
int sum = 0;
for(int i=0;i<nums.length;i++){
sum+=nums[i];
if(sum==total){
return i;
}
total-=nums[i];
}
return -1;
}
}
- 时间复杂度:O(N)
- 空间复杂度:O(N)
2. 解法2:前缀和
思路
记数组的全部元素之和为total,当遍历到第i个元素时,设其左侧元素之和为sum,则其右侧元素之和为 total - nums[i] - sum。左右侧元素相等即为 sum = total = nums[i] - sum,即 2 * sum + nums[i] = total
class Solution {
public int pivotIndex(int[] nums) {
// 前缀和
int total = Arrays.stream(nums).sum();
int sum = 0;
for(int i=0;i<nums.length;i++){
if(2 * sum + nums[i] == total){
return i;
}
sum+=nums[i];
}
return -1;
}
}
- 时间复杂度:O(N)
- 空间复杂度:O(N)
3、删除排序数组中的重复项
一个有序数组 nums,原地删除重复出现的元素,使每个元素只出现一次,返回删除后的数组的新长度。
不能使用额外的数组空间,必须在原地修改输入数组并在使用O(1)额外空间的条件下完成。
输入:[0,1,2,2,3,3,4]
输出:5
1. 解法1:双指针
思路
数组完成排序后,我们可以放置两个指针 i 和 j,其中 i 是慢指针,而 j 是快指针。只要 nums[i] = nums[j],我们就增加 j 以跳过重复项。
当遇到nums[j] != nums[i] 时,跳过重复项的运动已经结束,必须把nums[j]的值赋值到nums[i+1],然后递增 i,接着再次重复相同的过程,直到 j 到达数组的末尾为止。
class Solution {
public int removeDuplicates(int[] nums) {
if(nums.length == 0){
return 0;
}
int i = 0;
for(int j = 1;j<nums.length; j++){
if(nums[i] != nums[j]){
i++;
nums[i] = nums[j];
}
}
return i+1;
}
}
- 时间复杂度:O(N)
- 空间复杂度:O(1)
4、素数个数统计
统计n以内的素数个数
素数:只能被1和自身整除的自然数,0 和 1 除外
输入:100
输出:25
1. 解法1:暴力
直接从2开始遍历,判断是否能被2到自身之间的数整除
// 暴力解法
public static int bf(int n) {
int count = 0;
for (int i = 2; i < n; i++) {
count += isPrime(i) ? 1 : 0;
}
return count;
}
public static boolean isPrime(int x) {
for (int i = 2; i < x; i++) {
if (x % i == 0) {
return false;
}
}
return true;
}
其中 isPrime可以优化循环次数
public static boolean isPrime(int x){
// 若i能被x整除,则x/i一定能被整除,因此只需判断i和根号x之中较小的即可
for(int i = 2; i * i <= x; i++){
if(x % i == 0){
return false;
}
}
}
- 时间复杂度:O(N^2)
- 空间复杂度:O(1)
2. 解法2:埃筛法
public static int eratosthenes(int n){
// 创建一个boolean类型的数组
boolean [] isPrime = new boolean[n];
int ans = 0;
for(int i = 2; i < n; i++){
if(!isPrime[i]){
ans += 1;
for(int j = i * i ; j < n; j += i){
isPrime[j] = true;
}
}
}
return ans;
}
- 时间复杂度:O(N^2)
- 空间复杂度:O(N)
将合数标记为true,j = i * i 从 2 * i 优化而来,系数2会随着遍历递增(j += i,相当于递增了系数2),每一个合数都会有两个比本身要小的因子(0,1除外),2 * i 必然会遍历到这两个因子
当2递增到大于根号n时,其实后面的已经无需再判断(或者只需判断后面一段),而2到根号n、实际上在 i 递增的过程中已经计算过了,i 实际上就相当于根号n
例如:n = 25 会计算以下
2 * 4 = 8
3 * 4 = 12
但实际上8和12已经标记过,在n = 17时已经计算了 3 * 4,2 * 4
5、x的平方根
在不使用sqrt(x)的函数的情况下,得到x的平方根的整数部分。
输入:x = 4
输出:2
输入:x = 8
输出:2
解释:8 的算术平方根是 2.82842…, 由于返回类型是整数,小数部分将被舍去。
1. 解法1:二分查找
思路
x 的平方根肯定在 0 ~ x 之间,使用二分查找定位该数字,该数字的平方一定最接近x的,m平方值如果大于x,则往左找,如果小于等于x,则往右找
找到 0 ~ x 的最中间的数m
如果 m * m > x,则m取 x/2 ~ x 的中间数字,直到 ,m * m <x,m则为平方根的整数部分
如果 m * m <= x,则取 0 ~ x/2 的中间值,直到两边的界限重合,找到最大的整数,则为x平方根的整数部分
// 二分查找
public static int mySqrt(int x) {
int index = -1;
int l = 0;
int r = x;
while (l <= r) {
int mid = l + (r - l) / 2;
if ((long) mid * mid <= x) {
index = mid;
l = mid + 1;
} else {
r = mid - 1;
}
}
return index;
}
- 时间复杂度:O(logN)
- 空间复杂度:O(1)
2. 解法2:牛顿迭代
假设平方根是 i ,则 i 和 x/i 必然都是x的因子,而 x/i 必然等于 i ,推导出 i + x / i = 2 * i,得出 i = (i +x / i) / 2
由此得出解法,i 可以任选一个值,只要上述公式成立,i 必然就是x的平方根,如果不成立, (i + x / i) /2得出的值进行递归,直至得出正确解
public static int newton(int x){
if(x==0) return 0;
return ((int)(sqrts(x,x)));
}
public static double sqrts(double i,int x){
double res = (i + x / i) / 2;
if(res == i){
return i;
}else{
return sqets(res,x);
}
}

























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








