理解与实现二叉搜索树-优快云博客

本文详细介绍了二叉搜索树的基本概念，包括其性质和结构。并提供了一个C++实现的二叉搜索树模板类，包括查找、插入和删除操作。通过这个实现，读者可以深入理解二叉搜索树的工作原理。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

二叉搜索树概念

二叉搜索树需要具备以下性质：

若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树

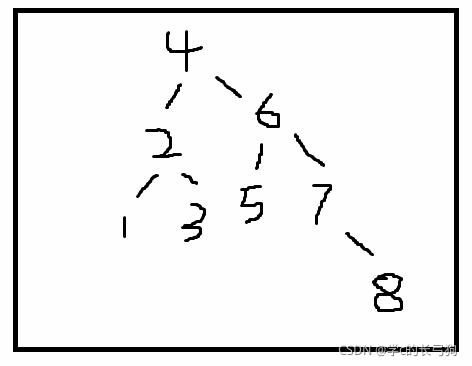
按照概念可知如图就是二叉搜索树。

二叉搜索树的实现

template<class T>
struct BSTNode
{
  BSTNode(const T& data = T())
      :_pLeft(nullptr),_pRight(nullptr),_data(data)
  {}
  BSTNode<T>* _pLeft;//LeftTree
  BSTNode<T>* _pRight;//RightTree
  T _data;
};

template<class T>
class BSTree
{
  typedef BSTNode<T> Node;
  typedef Node* PNode;
public:
  BSTree():_pRoot(nullptr)
  {}
  ~BSTree();
  {
    
  }
  PNode Find(const T& data)
  {
    if(data == _pRoot.data)
      return true;
    while(data < _pRoot.data)
    {
      _pRoot = _pRoot._pLeft;
      if(data == _pRoot.data)
        return true;
    }
    while(data > _pRoot.data)
    {
      _pRoot = _pRoot._pRight;
      if(data == _pRoot.data)
        return true;
    }
    return false;
  }
  bool Insert(const T& data)
  {
    if(nullptr == _pRoot)
    {
      _pRoot = new Node(data);
      return true;
    }
    PNode pCur = _pRoot;
    pNode pParent = nullptr;
    while(pCur)
    {
      pParent = pCur;
      if (data < pCur->_data)
        pCur = pCur->_pLeft;
      else if (data > pCur->_data)
        pCur = pCur->_pRight; // 元素已经在树中存在
      else
        return false;
    }
    pCur = new Node(data);
    if (data < pParent->_data)
      pParent->_pLeft = pCur;
    else
      pParent->_pRight = pCur;
      return true;
    }
  bool Erase(const T& data)
  {
    if (nullptr == _pRoot)
      return false;
    PNode pCur = _pRoot;
    PNode pParent = nullptr;
    while (pCur)
    {
      if (data == pCur->_data)
        break;
      else if (data < pCur->_data)
      {
        pParent = pCur;
        pCur = pCur->_pLeft;
      }
      else
      {
        pParent = pCur;
        pCur = pCur->_pRight;
      }
    }
    if (nullptr == pCur)
      return false;
    if(nullptr == pCur._pRight)
    {
      if(nullptr == pCur._pLeft)
        delete pCur;
      else
        pCur.pLeft= pParent.pLeft;
        delete pCur;
    }
    else if (nullptr == pCur->_pLeft)
    {
      if(nullptr == pCur._pRight)
        delete pCur;
      else
        pCur.pRight= pParent.pRight;
        delete pCur;
    }
    else
    {
      pCur = pCur.pRight; 
    }
    return true;  
  }

private:
  PNode _pRoot;
};