【包含所有题目】第十五届蓝桥杯大赛软件赛省赛（研究生组--C语言）

原创已于 2025-04-05 18:09:03 修改 · 2.2k 阅读

35 ·

CC 4.0 BY-SA版权

文章标签：

#蓝桥杯

于 2025-03-27 17:18:29 首次发布

数据结构专栏收录该内容

4 篇文章

订阅专栏

题目一：劲舞团（填空题）

问题描述

小蓝最近迷上了一款名为 “劲舞团” 的游戏，具体来说，只要按照游戏中给出的键位提示依次按出对应的键位，游戏人物便可以跟随节奏跳舞。对于连续的 K 次正确敲击，如果任意连续的两次敲击间间隔时间都小于等于1s，那么我们称这是一次 K 连击。现在给出一局小蓝的游戏记录文件，log.txt 中记录了 N 条记录，每条记录有三个字段，依次为正确的敲击字符、小蓝打出的字符、打出字符的时间对应的毫秒时间戳。现在请你计算下最长的 K 连击是多少，你只需要输出 K 的值。

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

答案

题目二：召唤数学精灵（填空题）

问题描述

数学家们发现了两种用于召唤强大的数学精灵的仪式，这两种仪式分别被称为累加法仪式 A(n) 和累乘法仪式B(n)。
累加法仪式 A(n) 是将从 1到 n 的所有数字进行累加求和，即：
A(n)=1+2+⋯+n
累乘法仪式 B(n) 则是将从 1 到 n 的所有数字进行累乘求积，即：
B(n)=1×2×⋯×n
据说，当某个数字 i 满足 A(i)−B(i) 能被 100 整除时，数学精灵就会被召唤出来。

现在，请你寻找在 1 到 2024041331404202 之间有多少个数字 i，能够成功召唤出强大的数学精灵。

答案提交

这是一道结果填空题，你只需要算出结果后提交即可。本题的结果为一个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

答案

思路：
满足 A(i)−B(i) 能被 100 整除，那么 A(i)和B(i)分别能被100整除，由代码得知当i >=10时，s所有结果刚好被100整除，，所有先求出前十个数里面有2个符合条件，然后对于10之后的数字，只需找出A(i)能被100整除，因为A(i)= i * (i + 1) / 2，A(i)要被100整除，则A(i)就是100的倍数，
那么， 2 * A(i) = i * (i + 1)，2 * A(i) 200的倍数，等价于A(i) 是100的倍数，i+200 或者 i-200 不会影响a1是200的倍数，故200是一个循环。

#include <stdio.h>
#include <stdlib.h>

//求n阶 
int main(int argc, char *argv[]) {
	int i,sum=1;
	for(i=1;i<=10;i++){
		sum *= i;
	} 
	printf("%d",sum);
	return 0;
}
结果：3628800

效果图

第一个为10到200

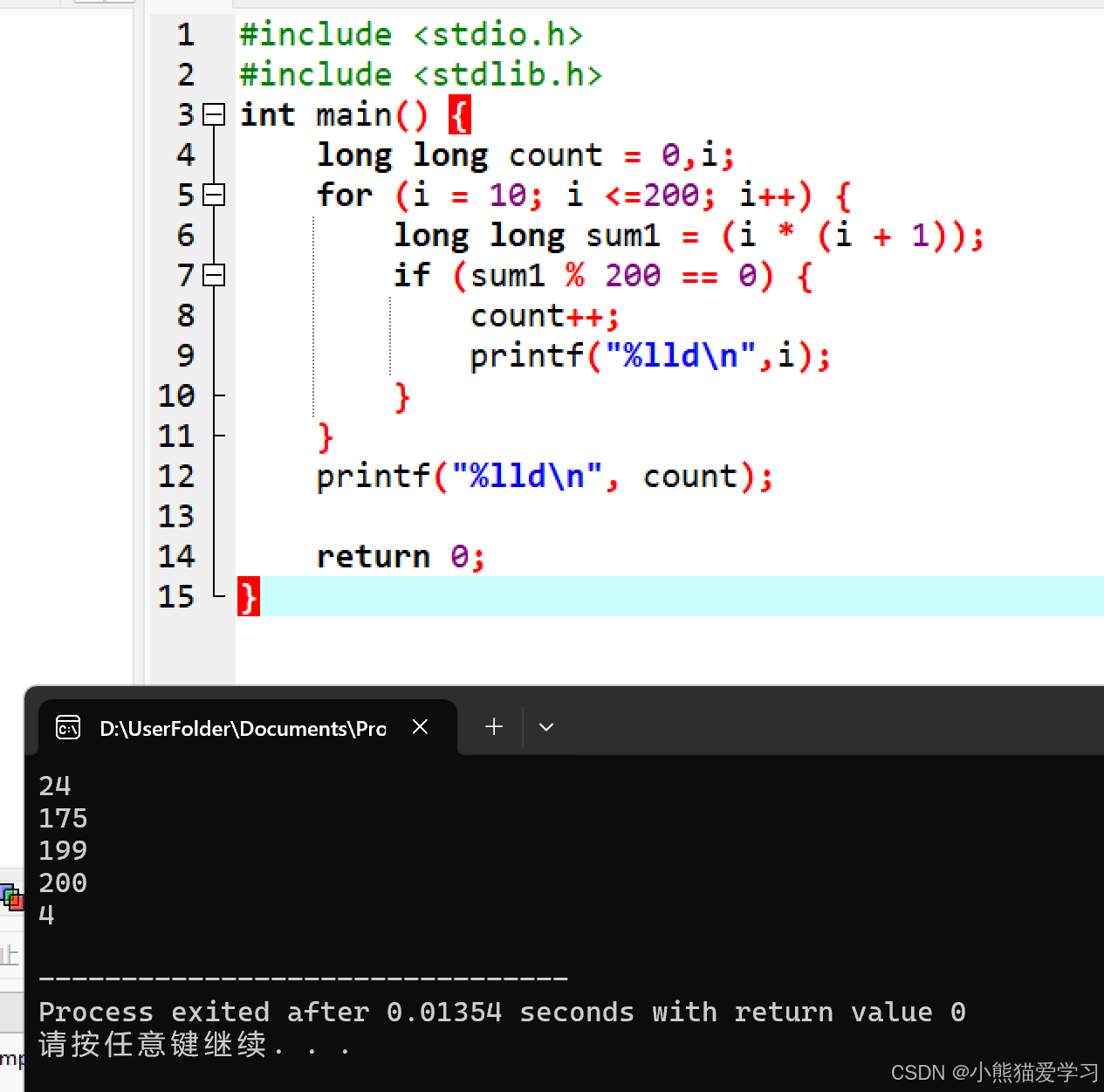
第二个为201到400
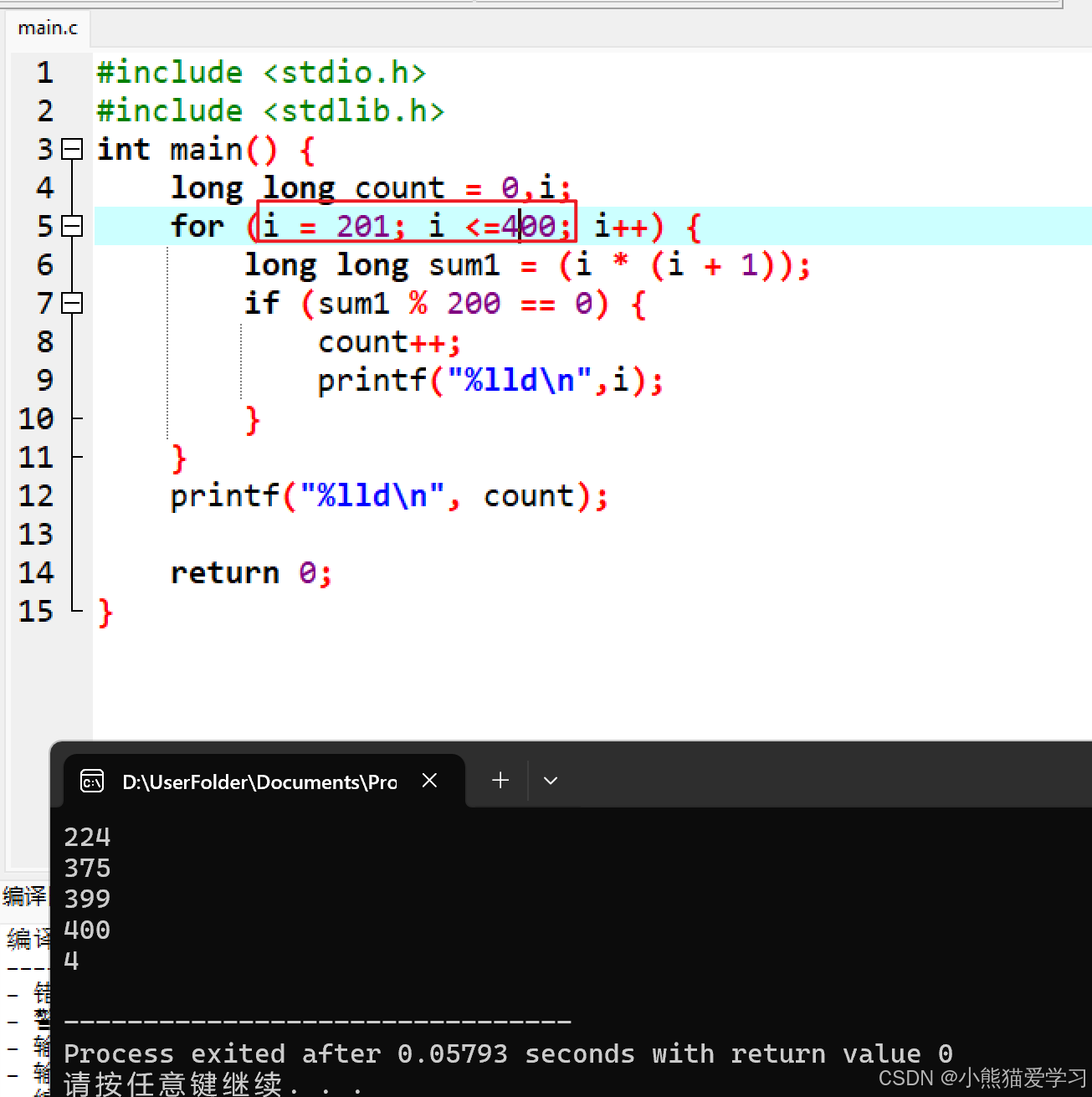
200到400

答案

40480826628086

#include <stdio.h>
#include <stdlib.h>

int main(int argc, char *argv[])
{
  // 请在此输入您的代码
  long long num=2024041331404202 / 200 *4 + 2;
  printf("%lld",num);
  return 0;
}
结果：40480826628086

题目三：封闭图形个数

问题描述

在蓝桥王国，数字的大小不仅仅取决于它们的数值大小，还取决于它们所形成的“封闭图形”的个数。

封闭图形是指数字中完全封闭的空间，例如数字 1、2、3、5、7 都没有形成封闭图形，而数字 0、4、6、9分别形成了 1 个封闭图形，数字 8 则形成了 2 个封闭图形。值得注意的是，封闭图形的个数是可以累加的。例如，对于数字 68，由于 6 形成了 1 个封闭图形，而8 形成了 2 个，所以 68 形成的封闭图形的个数总共为 3。

在比较两个数的大小时，如果它们的封闭图形个数不同，那么封闭图形个数较多的数更大。例如，数字 41 和数字 18，它们对应的封闭图形的个数分别为 1 和 2，因此数字 41 小于数字 18。如果两个数的封闭图形个数相同，那么数值较大的数更大。例如，数字 14 和数字
41，它们的封闭图形的个数都是 1，但 14<41，所以数字 14 小于数字 41。如果两个数字的封闭图形个数和数值都相同，那么这两个数字被认为是相等的。

小蓝对蓝桥王国的数字大小规则十分感兴趣。现在，他将给定你 n 个数
a1,a2,…,an ，请你按照蓝桥王国的数字大小规则，将这 n 数从小到大排序，并输出排序后结果。

输入格式

第一行包含一个整数 n，表示给定的数字个数。
第二行包含 n 个整数 a1,a2,…,an，表示待排序的数字。

输出格式

输出一行，包含
n 个整数，表示按照蓝桥王国的数字大小规则从小到大排序后的结果，每两个数字之间用一个空格分隔。

样例输入

3
18 29 6

样例输出

6 29 18

样例说明

对于给定的数字序列 [18,29,6]，数字18 的封闭图形个数为 2，数字 29 的封闭图形个数为
1，数字 6 的封闭图形个数为 1。按照封闭图形个数从小到大排序后，得到 [29,6,18]。

由于数字 29 和数字 6 的封闭图形个数相同，因此需要进一步按照数值大小对它们进行排序，最终得到[6,29,18]。

评测用例规模与约定

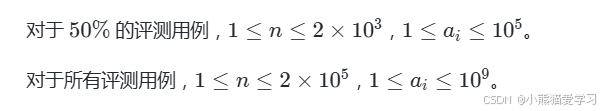
在这里插入图片描述

代码

#include <stdio.h>
#include <stdlib.h>
// 思路：定义结构体，先判断封闭空间个数，先利用qsort排序，如果空间个数相等再单独拿出来排序。

//定义结构体
struct number{
  int x; //数字
  int y; //存储封闭空间数
};

// 计算封闭空间数的函数
int abc(int num){
  int count = 0; //每算完一次，初始化为0
  if(num < 0) num = -num; // 处理负数
  if(num == 0){
    return 1;
  }
  while(num != 0){
    if(num % 10 == 0 || num % 10 == 4 || num % 10 == 6 || num % 10 == 7 || num % 10 == 9){
      count ++;
    }else if(num % 10 == 8){
      count += 2;
    }
    num /= 10;
  }
  return count;
}
//qsort比较函数,用于比较两个整数
int funcmp(const void *a, const void *b){
  const struct number *num1 = (const struct number*)a;
  const struct number *num2 = (const struct number*)b;
  //先按照空间数升序排序
  if(num1->y != num2->y){
    return num1->y - num2->y;
  }
  //如果空间数相等，则按照数字大小升序排序
  return num1->x - num2->x;
}
int main(int argc, char *argv[])
{
  int n, i;
  scanf("%d",&n);
  struct number *array1 = malloc(n * sizeof(struct number));//根据输入的数字个数来定义数组大小
  for(i=0;i<n;i++){ 
    scanf("%d",&array1[i].x);
    array1[i].y = abc(array1[i].x); //计算空间个数
  }

    // 使用qsort进行排序
    qsort(array1, n, sizeof(struct number), funcmp);

    //打印
    for(i=0; i<n; i++){
      printf("%d ",array1[i].x);
    }
    printf("\n");
    free(array1);
  return 0;
}