强化学习的数学原理

​
参考教程：https://www.bilibili.com/video/BV1sd4y167NS
赵老师yyds！

文中会有部分是英文，不是装逼而是个人认为原版的英文更适合去理解其本质，翻译过来就变得难以理解了！

强化学习介绍与基本概念

1、强化学习介绍

强化学习是一类算法，是让计算机实现从一开始完全随机的进行操作，通过不断地尝试，从错误中学习，最后找到规律，学会了达到目的的方法。这就是一个完整的强化学习过程。让计算机在不断的尝试中更新自己的行为，从而一步步学习如何操自己的行为得到高分。

监督学习、无监督学习的目标是做分类和回归，强化学习目标是求解最优策略。

2、基础概念解释

（1）基本名词

[1] state： The status of agent with respect to(相对于) the environment
[2]state space： the set of all states
[3] action： For each state，there are some possible actions
[4] action space of a state： the set of all possible actions of a state(action space和state是依赖关系,不同state的action space是不一样的)
[5] state transition： A process while taking an action，the agent may move from one state to another
[6] state transition probability： use probability to describe state transition(p(s₂|s₁,a₁)=1，条件概率的引入就可以描述随机状态而不是只可以描述确定状态)
[7] policy： tells the agent what actions to take at a state，mathematical representation of policy： using conditional probability(π(a₁|s₁)=1，可以描述随机情况还可以描述确定情况)
[8] reward： a real number we get after taking an action(reward是我们和agent交互的手段,通过设计reward来实现我们的目标) mathematical representation of reward： using conditional probability(p(r=-1|s₁,a₁)=1，reward依赖于当前action和state而不是下一个state)
[9] trajectory： A state-action-reward chain
[10] return： the sum of all the rewards collected along the trajectory(return常用来评价一个policy的好坏) discounted return： introduce a discount rate γ∈[0,1)(γ用来衡量短期reward和长期reward，通过控制γ可以控制agent所学的policy)
[11] episode： The trajectory which has some terminal states is called an episode(有些任务是没有terminal states会一直执行被称为continuing tasks，研究过程中通常把continuing tasks转换成episode，就是把terminal state当作普通的state考虑在policy中，进入到这个state就获得奖励)

（2）Markov decision process（MDP）

Markov->Markov property；decision->policy；process->state transition probability+reward probability(过程：从xx状态到xx状态采取xx动作获得xx奖励)

Markov decision process becomes Markov process once the policy is given!

贝尔曼公式

1、State value的定义

state value：是对discounted return的期望(或叫做平均值)代表的是这个状态(这个状态要是已知的)的价值，从这个状态出发会得到更多的d return。d return是针对单个trajectory而state value 是对多个trajectory得到的d return求平均值(如果从一个state出发每一步都是确定的那么只有一个trajectory，此时return等于state value)state value公式为：v_π(s)=E[G_t|S_t=s]（R是奖励、G是d return）

2、Bellman Equation详细推导

所谓的Bellman Equation就是用来描述不同状态的state value之间的关系
根据state value的定义来推导Bellman Equation公式
先计算第一项：（计算就是用概率把期望展开）
确定了当前状态s，求获得的immediate reward的期望=所有可能的动作 X 当前状态采取每个动作后的奖励的期望=所有可能的动作 X ( 当前状态采取每个动作后得到的每个奖励值 X 获得这个奖励的概率)
然后再计算第二项：
确定了当前状态s，下一时刻所得的return的期望=下一时刻所有可能的状态 X 当前状态s下一时刻状态s·的return的值的期望= 下一时刻所有可能的状态 X 下一时刻状态s·的return的值的期望(Markov property)=下一时刻所有可能的状态 X 下一时刻的s·的state value=当前时刻到下一时刻采用不同动作的概率 X 选用了某个动作后跳到某个时刻的概率 X 下一时刻的s·的state value

也就是 immediate reward+future rewards
Bellman Equation不是一个式子而是对于状态空间中的所有状态都成立，n个状态就有n个Bellman Equation，再通过这n个Bellman Equation求出state value(有两种求解方法)

π(a|s)、p(r|s,a)、p(s`|s,a)分别是policy、reward probability和state transition probability。Bellman equation需要依赖给定的policy才能计算

贝式方程变为policy✖[reward probability✖reward+γ✖state transition probability✖state value]（加号前是状态s，加号后是下一刻状态s`）

3、Bellman Equation(公式向量形式求解)

r_π表示从当前状态出发所能得到的immediate reward的平均值，p_π表示从s_i转换到s_j的概率与s_j的state value之积

变成matrix-vector form便于计算，即v_π=r_π+γP_πv_π

4、用Bellman Equation求解state value

给定一个policy，列出贝尔曼公式求解得到state value，用来衡量该policy的好坏
求解state value有两种方式：利用矩阵逆求解析表达式和迭代

通过实例来讲解怎么求解Bellman Equation：

先列出所有状态的bellman equation，如果状态比较少可以直接解出来，如果状态比较多则采用迭代去求解。

5、Action value

state value是从一个状态出发agent获得的return均值，而action value是从一个状态出发选择了一个action后得到的return均值。就像state value一样，action value是用来判断哪个action价值大

q_π(s,a)是a function of the state-action pair(s,a)，它与state value的关系是state value=好多action的action value用概率求期望

即，从一个状态出发的state value=从该状态出发选择不同action得到的action value的平均值

式子2说明知道了一个状态的所有action value求平均就是这个状态的state value；式子4说明如果知道所有的state value就能得到所有的action value。这个式子提供了两种计算action value的方法

6、Summary

贝尔曼最优公式

1、怎样去衡量给定的policy

state value可以衡量一个policy的好坏，具体数学公式表示是：

而最优策略是指该策略相比任意的其它策略π在每个状态得到的state value都是最大的，即：

2、Bellman optimality equation（BOE）贝尔曼最优公式

（1）BOE的表达式

elementwise form：

matrix-vector form：

BOE中v是未知量，π也是未知需要求的

（2）求解BOE

求解BOE公式中的maxπ的方法是先固定v然后求解π，把BOE转化成了v的函数
先引入一些概念，[1]Fixed point： x∈X is a fixed point of f： X—>X if f(x)=x [2]Contraction mapping： f is a contraction mapping if ||f(x₁)-f(x₂)||≤γ||x₁-x₂|| where γ∈(0,1)

然后举两个例子来理解这两个概念：

最后引出Contraction mapping theorem：

根据Contraction mapping theorem定义可以证明BOE： v=f(v)=maxπ(r_π+γP_πv)的f(v)是contraction mapping
根据Contraction mapping theorem性质可以求解出，BOE一定存在唯一解v^*且可以通过迭代公式v_k+1=f(v_k)=maxπ(r_π+γP_πv_k)求解出来（v_k其实是最优值v_*的估计，v_k最后是会收敛到v_*当k趋于∞）

将迭代与BOE公式结合可以得到： a₁a₂a₃是三个动作，大小关系是a₂>a₃>a₁，概率分别是p₁p₂p₃，p₁+p₂+p₃=1，max[p₁xa₁+p₂xa₁+p₃xa₃]的结果就是让a₂的概率为1，其余的概率为0。

对于v_π=Σπ(a|s)q_π(s,a)，如果要让state value最大则根据上面的推理可知要令最大的q_π(s,a)的π(a|s)为1，取余的q_π(s,a)的π(a|s)为0。因此求解BOE就变成了找最大的q_π(s,a)，采用公式q_π(s,a)=Σ_r r*p(r|s,a)+Σ_s· p(s·|s,a)v_π(s·)求出q_π(s,a)，然后根据最大的q_π(s,a)指定策略π，再利用q_π(s,a)和π求出各个状态的v_π(s)然后进行新一轮的找到最大q_π(s,a)、更新π、求出v_π(s)…初始各个状态的v_π(s)随便设，一般设为0

整个求解流程：求解目标是v^*(sⁱ)和π^*，k=0时设置初始state value值为0（v₀(s_i)=0），然后算出q_π(s,a)[利用的是action value的公式(4)]，根据最大的q_π制定策略π(a_j|s_i)，再计算出v₁(s_i)[利用的是迭代公式]；进入下一轮迭代，利用v₁(s_i)计算出q_π(s,a)，根据最大的q_π制定策略π(a_j|s_i)，再计算出v₂(s_i)；再进入下一轮迭代，利用v₂(s_i)计算出q_π(s,a)，根据最大的q_π制定策略π(a_j|s_i)，再计算出v₃(s_i)；…直到||v_k-v_k-1||≤提前设置的阈值就停止迭代

一个Bellman equation对应的是一个策略，而BOE对应的是最优策略，所以BOE是一个特殊的BE，BOE的state value是所有state value最大的。v^*求解出来后代入BOE可以求出π^*

π^*为：它是deterministic、greedy(每次只选择action value最大的action)的

（3）分析BOE

思考：哪些因素会决定最优策略？

改变r或者γ会影响最优策略，p(r|s,a)和p(s`|s,a)是系统设定的通常不轻易改变。而且r改变影响policy起作用的不是absolute value而是relative value，γ的存在可以约束agent在最短时间完成，避免agent绕路 ！如果一个state周围的states的policy已经达到最优，那么这个state也能达到最优

core：π^*是通过v^*求解的，v^*是利用v₀=0，v₁，v₂…迭代出来的，v的迭代是用q_π来进行的(选出最大的q_π作为下一轮v的值)，因为知道v₀就可以求出q₀的值了。v^*是唯一的但π^*不是唯一的

值迭代与策略迭代

1、Value Iteration（值迭代算法）

所谓的value iteration就是求解BOE

（1）value iteration algorithm

（分两步走，先根据q_π选出π_k+1，再计算出v_k+1）

v_k并不是一个state value，只是在求解过程中的一个数值。matrix-vector form通常用来理论分析，elementwise form是用来研究如何实现

Step1：

Step2：

（2）伪代码

2、Policy Iteration（策略迭代算法）

（1）policy iteration algorithm

先根据π_k求解出v_πk(就是求解Bellman equation)，然后求解argmax优化问题求出新策略π_k+1

算法工作流程：start from π₀

policy iteration是一个迭代算法，而policy evaluation是policy iteration的一步，policy evaluation本身又依赖一个迭代的算法

Step1：这一步是利用π_k找到v_πk，这一步的迭代是在通过求解Bellman equation来求解state value，求bellman可以迭代也可以直接求。首先先把各个状态的Bellman equation列出来，简单的一眼就看出来了，复杂的可能需要迭代一下。

v_πk^j代表第j个iteration估计出来的v_πk的值，π_k(a|s)、p(r|s,a)、p(s^`|s,a)都是已知的，迭代求出下一个(j+1)iteration估计出的v_πk的值，直到收敛

Step2：利用上一步找到的v_πk来更新π_k+1

（2）伪代码

在某一个状态选择最大action value的a，严重依赖于其他状态的策略，如果其他状态的策略是不好的那么即使选了最大的action value也是没有意义的。

3、Truncated Policy Iteration（截断策略迭代算法）

（1）Compare

这两种算法非常类似，Pi是从π₀出发，先计算出v_π0的值(by solving Bellman equation)，然后更新π₁(by solving the BOE,即用v算q然后每个s选q最大的a构成最优策略)；Vi是从v₀出发，首要是计算q₀更新π₁(求解BOE,即用v算q然后每个s选q最大的a构成最优策略)，再更新v₁(by the relationship of state value and action value,即v_π(s)=Σπ(a|s)q_π(s,a)结合最优策略下状态的state value值最大,即v_k+1=q_kmax)

（2）truncated policy iteration

特别之处在求解state value v_π(s,a)，value iteration是只迭代一次(求解BOE)得到state value v_π(s,a)；policy iteration是迭代了∞次(求解BE)得到state value v_π(s,a)，

（3）伪代码

在truncated policy iteration的大迭代中嵌套的小迭代次数，value iteration是1次；policy iteration是∞次

4、Summary

Value iteration就是求解BOE问题，只不过规定了两个步骤，换了种说法

蒙特卡洛方法

1、蒙特卡洛的不同之处

前一章的value iteration和policy iteration统称为model-based reinforcement learning，更准确地来说应该称为dynamic programming的方法。MBRL是用数据估计出来一个模型，然后基于这个模型来进行强化学习，像之前提到的p(r|s,a)、p(s`|s,a)都是model parameters，是事先知道的。

而蒙特卡洛算法是model-free的，即事先并不知道模型的参数。

2、Monte Carlo estimation

凡是需要做大量的采样然后实验，最后用实验的结果进行近似都可以称为Monte Carlo estimation。大数定律已经证明了对于大量的实验得到的结果所求的平均值对于该实验变量期望是无偏估计的。故我们用Monte Carlo去估计expectation来得到state value和action value

Monte的思想是：通过多次采样随机变量得到数据，将数据的平均值作为随机变量的期望

3、MC Basic（The simplest MC-based RL algorithm）

核心问题是怎么把依赖模型的部分替换成model-free的模块！

先看policy iteration，基于model计算action value是需要知道p(r|s,a)和p(s`|s,a)，如果按照action value的定义E[G_t|S_t=s,A_t=a]来看，用MC estimation来得到action value：从(s,a)出发得到大量的episode，对所得episode的return求平均

MC Basic is useful to reveal the core idea of MC-based model-free RL，but not practical due to low efficiency！MC Basic是直接得到action value(跳过policy iteration中先算出state value的步骤)，然后去更新policy(选择action value大的动作)

伪代码：state-action-pair(s,a)的个数=the sum of states ✖ the sum of actions 一个(s,a)可以有n条轨迹即s_i下采取a_i后可以随便走，随便走的这些轨迹的return均值代表了q_π(s_i,a_i)

episode length很短的时候，只有离目标很近的状态才能到达目标，随着episode length变大，离目标越来越远的那些状态也能慢慢的到达目标。因此episode length需要足够长但也不需要太长

4、MC Exploring Starts

（1）改进方向一，让数据的利用更加高效

引入visit：每次遍历到一个state-action pair称为对此(s,a)的一次visit

在MC Basic中用到的是Initial-visit method，即对于一个episode只考虑开头的(s,a)，用剩下的(s,a)所得的return来估计开头(s,a)的action value。这种method最大的问题就是没有利用好数据，良好的利用方式应该是下面的：即every-visit method

（2）改进方向二，更加高效地去更新策略

在MC Basic中用到的是把所有的episode(从一个state-action pair出发的)全部收集到后做一个average return来估计action value。缺点是要等所有的episode收集完成后才行

另一种方法是得到了一个episode后就立刻用这个episode的return来估计action value然后不等了，直接开始改进策略，这样得到一个episode就改进策略会提升效率(一个episode去估计action value虽然不精确但是没有关系，truncated policy iteration在求解Bellman equation也是这样子的)

（3）MC Exploring Starts（计算效率更高的MC Basic）

倒着算，计算的公式是return： R=r+γR；如果此时的(s,a)不在前面的state-action pair，表面这是它最后一次出现则要开始计算它的q_π(s,a)了，

Why do we need to consider exploring starts？

exploring(确保每一个(s,a)都要被访问到)是指从每个(s,a)出发，都要有episode，只有这样才能用后边生成的reward来估计return，进一步估计action value；starts是指估计当前(s,a)的return是从当前(s,a)开始的，还有一种估计当前(s,a)的return的方法是从某个(s,a)开始的episode包含当前(s,a)（还有一种叫visit的访问方法是指从其他的(s,a)出发，但是能够经过当前的(s,a)。）visit不常用因为不能保证一定有episode经过当前的(s,a)

5、MC ε-Greedy

把exploring starts这个条件去掉，之前是greedy的即只选最大

（1）引入soft policy

引入soft policy后，使得对每一个action都有可能去做选择，soft policy属于stochastic policy。对于soft policy来说，从一个state-action pair出发，如果产生的episode很长加上soft policy是探索性的故能确保任何一个(s,a)都能在这个episode访问到(因此可以去掉exploring starts)

采用ε-greedy(soft policy的一种) ：

也就是说，选择argmax_aq(s,a)的概率是第一个；选择非最大action value的取余action的概率是第二个(第一个概率很大，第二个概率很小，即虽然给了取余action选择的概率但是选择greedy action的概率是最大的)

使用ε-greedy，平衡了exploitation(选择最大的动作，充分利用已经求出的值 )和exploration(可能由于导致当前决策并不是最优的，需要具备随机探索能力，ε给了这种能力)

（2）ε-greedy结合MC

该改进方法是在policy improvement中，之前的policy是求出maxq_πk，让其对应的action概率为1其余为0。现在是求出maxq_πk后大概率选择其对应的action，还有小概率选择取余的action

伪代码：（和exploring starts相比采用了every-visit method以及更新policy时有所不同，其余都一样）

先生成一个episode然后再根据这个episode去算各个(s,a)的action value然后再选policy。MC Basic还是从一个s出发，把所有(s,a)走好多遍然后算各个(s,a)的action value然后再选policy。

但是，探索性的代价是牺牲了最优性(最优策略的定义是基于state value，最优策略是有最大的state value)，可以设置较小的ε进行训练；还可以刚开始设置一个比较大的ε，然后让ε逐渐趋于0。注意：ε不能太大

随机近似与随机梯度下降

1、mean estimation的两种求mean方法

现有一个random variable X，目标是估计其期望E[X]，收集一些iid的采样数据{x_i}^N(i=1)，可以用这些采样数据的均值来估计期望：

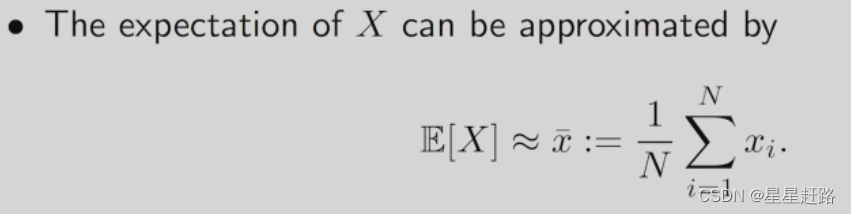
$$E[X]\approx \overline{x}（N->\infty ）$$
问题来了，怎么求平均值？

（1）收集到所有的采样数据求平均

（2）增量式迭代求平均数：(实时计算w_k，新采样的数据x_k直接通过公式计算出新的w_k+1)

具体的计算过程为：

刚开始w_k可能不精确但是也可以用，随着数据量越来越大，w_k也会越来越精确地逼近E[X]

更一般的，把1/k换成α_k，α_k就是一个正数，当α_k满足一些条件时可以保证w_k+1仍然逼近E[X]

2、Robbins-Monro algorithm

（1）Stochastic approximation（SA,随机近似算法）

SA代表了一大类的算法，具有随机、迭代的特点，涉及到对随机变量的采样，解决对方程的求解或优化问题

SA的优点是在不知道方程或者目标函数的表达式(即也不知道其导数或者梯度的表达式)进行求解

（2）Robbins-Monro (RM) algorithm

这是一个迭代式的算法

RM求解的是一个方程g(w)=0，其中g是函数但是并不知道表达式，只知道给一个w能求出一个输出g(w,η)，w是要求解的未知量，设最优解是w^*，随着k—>∞，w_k趋向于w_*。即w_k+1总要比w_k更接近w_*

举一个简单的例子：g(w)=tanh(w-1)，Parameters：w₁=3，a_k=1/k，η_k=0，the RM algorithm in this case is w_k+1=w_k - a_kg(w_k)

（3）RM算法收敛性的证明

下面给出严格的数学上的描述来说明为什么RM算法能够收敛，收敛定理：

w_k的收敛是概率意义上的收敛

首先，对于函数g有要求：(g的梯度要是大于0且有上限，不能一直增加)

其次，对于a_k也有要求：(最常见的满足条件的ak是1/k)平方和小于∞，和等于∞

最后，对于噪声η也有要求：

如果这三个条件不满足算法可能就失效了；实际工作中a_k会设置成一个很小的数而不是1/k

（4）将RM算法应用到mean estimation中

3、Stochastic gradient descent(是RM的一个特殊情况)

（1）SGD是特殊的RM算法

用途广泛，是特殊的RM算法，均值估计算法是特殊的SGD算法

（2）SGD解决的是优化问题

如果要最大化目标函数是梯度上升；最小化目标函数是梯度下降（f是一个包含变量w和随机变量X的函数，如f(w,X)=1/2||w-X||²，J是要最小化的函数，J达到最优的必要条件是其gradient等于0）

求解方法有3种：

GD：最优解是w_*，第k次估计值是w_k，这个值是不准确的但是可以在第k+1次更新

缺点是不知道expectation

BGD：用采样数据来对随机变量的期望用平均值估计

缺点是每次更新w_k的时候需要采样n次

SGD：只采样一次，用这一次的数据去估计期望SGD是把GD中的true gradient用stochastic gradient替换，SGD是知道函数梯度的采样

（3）举例说明

前面提到的mean estimation其实是特殊的SGD算法

写出其GD、SGD的形式：

（4）SGD收敛性证明

如果期望不知道就用一个采样去近似）

stochastic gradient=true gradient+error

通过证明SGD是一个特殊的RM算法，只要SGD满足RM的三个要求就可以证明其收敛性。

将求解最小化J(w)转换为求解g(w)=0问题，即g(w)=∇_wJ(w)=0=E[∇_wf(w,X)]（这是因为当J(w)最小化时其梯度一定为0）

问题转化为了怎么求g(w)=0，根据RM算法可知，w_k+1=w_k+g^~(w_k,η_k)，g^~(w_k,η_k)是对g(w)的一个含噪声的采样，我们的g^~(w_k,η_k)刚好是stochastic gradient，即为∇_wf(w_k,x_k)

SGD是特殊的RM算法，SGD的收敛性分析如下：

证明思想是让SGD往RM上靠近，SGD是min_w j(w)，RM是g(w)=0，使用最优化问题在达到最值时其梯度为0，对j(w)求梯度，令其为0就转为g(w)=0

RM变成SGD就是把g(w_k，η_k)变成(w_k—x_k)

（5）SGD的收敛随机性是否会很大？

即w⁰最后可以收敛到w^*但是最开始会朝完全相反或者随机方向迭代很多次才收敛呢？分析可知，并不会！

有意思的结论：当w_k距离w_*非常远的时候，SGD和普通的梯度下降是类似的；当接近w_k接近w_*的时候，SGD才会呈现出stochastic的性质

此外，我们实际求解的SGD问题的形式是：

x_i是一组数据而不是之前的是随机变量X的采样

（6）BGD vs MBGD vs SGD：

当m=1时，MBGD变成了SGD；当m=n时，MBGD并不完全是BGD，因为MBGD是随机抽样n个而BGD是所有的n个采样(可能有些数据被采样多次而有的数据一次都没被采样到)

举一个例子：

求出这个J(w)的BGD、MBGD、SGD

J(w)的BGD、MBGD、SGD分别如下：

收敛速度(即求出w_k+1)：BGD最快，MBGD其次，SGD最慢

4、Summary for stochastic approximation

RM是SA一个具有开拓性的领域；Mean estimation是SGD的特例；SGD是特殊的RM算法

时序差分方法

1、富有启发的数学思考

RM算法去求解E[R+γv(X)]，写成g(w)=0的形式然后用RM的公式去求解，RM里的噪声η用E[R+γv(X)]-[r+γv(x)]表示，则g^~(w,η)=g(w)+η=w-[r+γv(x)]

2、TD learning of state values

（1）算法的特点

该算法是求解一个给定的策略π的state values，为的是policy evolution。这个算法只能用来估计给的策略的state value而不能估计action value和搜索最优策略

该算法是基于数据的，数据为(s₀,r₁,s₁,r₂,s₂,…,s_t,r_t+1,s_t+1,…)或者是{(s_t,r_t+1,s_t+1)}_t，这些数据都是由给定的策略产生的

式子(2)表示t时刻未被访问到的s保持不变

TD target是说我们希望v_t能够朝着这个方向去修改；TD error是说现在的v_t与TD target的差距

（2）算法是model-free、属于RM算法的

TD算法是在没有模型的情况下求解Bellman equation；TD算法是求解Bellman equation的RM算法

先写出Bellman expectation equation： 关键一步是E[G|S=s]=E[v_π(s`)|S=s]

通过使用RM算法来求解Bellman expectation equation，转换成g(w)=0的形式

找到g(w)和g^~(w,η)后写成RM经典形式，即w_k+1=w_k-α_kg^~(w_k,η_k)

可以看出RM求解Bellman expectation equation的形式与TD算法非常类似，但仍然有两个不同点不同：1）需要反复得到{(s,r,s`)}，与TD算法基于episode的时序访问不一样2）v_π(s·_k)是未知的

解决方法：

1）得到一个trajectory，每次访问到s就去更新s，没访问到s时s的估计值保持不变；2）把v_π(s·_k)替换成v_k(s·_k)，还是可以确保收敛的

（3）TD learning VS MC learning

[1] online vs offline

离线是说采样得到的数据不能立刻用，需要等到episode结束才能计算从当前s到最后的return来作为return的估计值

[2] bootstrapping vs non-bootstrapping

bootstrapping是说在之前估计的基础上更新，依赖于初始值；non-bootstrapping是直接根据当前的episode来计算return然后用计算出的return直接作为估计值

3、TD learning of action values： Sarsa

Sarsa是估计出给定策略的action value，从而做到policy evaluation

（1） 无模型的就需要数据(experience)

q(s,a)是对q_π(s,a)的估计值；q_t(s,a)是对q_π(s,a)在t时刻的估计值

Sarsa和TD learning几乎一样，只不过是把对state value的估计改成了对action value的估计；Sarsa也是在求解Bellman equation，只不过是基于action value表达的，刻画的是不同action value之间的关系

收敛性：q_t(s,a)收敛于q_π(s,a)当t趋向于∞

定理只是告诉我们q_t收敛于q_π，即给定策略可以估计出其action value。如果想得到最优策略还是需要和policy improvement结合

伪代码：（更新策略采用ε-greedy）Sarsa是说从一个状态出发在没到达目的状态前，s_t根据策略π_t(s_t)选择a_t产生r_t+1和s_t+1，然后根据策略π_t+1(s_t+1)选择a_t+1，最后根据这些数据更新policy生成π_t+1

更新完action value会立刻进行策略的更新

从一个状态出发的最优策略和所有状态都最优的策略是不一样的。Sarsa和TD算法基本一样，只有两点区别：1）Sarsa是直接估计action value；2）把Sarsa和policy improvement结合得到一个能够搜索最优策略的算法

4、TD learning of action values： Expected Sarsa

Expected Sarsa是Sarsa的变形

（1）Expected Sarsa

相比于Sarsa，增加了计算量；去掉了a_t+1减少了随机变量的个数，不需要再对a_t+!进行采样了，减少了随机性

（2）Expected Sarsa也是在求解Bellman equation

Bellman equation(又一种形式)：q_π(s,a)=E[R_t+1+γv_π(S_t+1)|S_t=s,A_t=a]

5、TD learning of action values： n-step Sarsa

n-step Sarsa也是Sarsa的变形

n-step Sarsa统一了Sarsa和MC learning，从action value的定义式出发，思考G_t的多种表达式：

G⁽¹⁾代入action value定义式中是Sarsa；G^(∞)代入action value是MC learning

Sarsa和MC learning都需要数据，但是不同的是Sarsa是在t时刻得到(s_t , a_t , r_t+1 , s_t+1 , a_t+1)就可以更新q_π；而MC learning需要走完一个episode才能求均值估计q_π

n-step Sarsa是一种折中，t时刻时，不仅需要t时刻的(s_t , a_t , r_t+1 , s_t+1 , a_t+1)，还需要t+n时刻的数据才能去对q_π(s_t , a_t)更新，所以Sarsa只能等待

n-step Sarsa是Sarsa和MC learning的混合：

6、TD learning of optimal action values： Q-learning

Q-learning不需要policy evolution和policy improvement结合，因为它直接就把最优的action value给估计出来

Q-leaning与Sarsa结构类似，只是TD target变了

Q-learning中的TD target是选择是action value最大的a；Sarsa中的TD target是根据策略选择的a

Q-learning在数学上是为了求解Bellman optimality equation

BOE有两点变化：1）有expectation；2）基于action value

Q-learning求解的是BOE，最后得到的q值是最优的策略对应的q值

Q-learning的伪代码：

1）on-policy version：

2）off-policy version： π_b是behavior policy

如果behavior policy的探索性很差那么target policy的更新也不会很好

7、off-policy VS on-policy

（1）behavior VS target

behavior policy：与环境交互生成experience；target policy：一直在迭代更新，最后是我们想要的策略

（2）判断on还是off

如果behavior policy和target policy是同一个策略(用一个策略和环境交互产生experience然后再改进这个策略，改进完了再用这个策略和环境进行交互)，则称为on-policy；如果behavior policy和target policy不是同一个策略(用一个策略和环境交互产生experience，然后将产生的experience训练另一个policy)

（3）常见算法的判断

Sarsa是on-policy，产生(s_t , a_t , r_t+1 , s_t+1 , a_t+1)里面的a_t+1的策略就是我们下一步去更新的策略，即有一个π_t，用它去生成experience(s_t , a_t , r_t+1 , s_t+1 , a_t+1)，然后利用experience去估计q_t+1，再利用q_t+1去改进π_t得到π_t+1

MC learning是on-policy，即有一个π，用它去生成一个trajectory，然后用trajectory得到的return来估计q_π，再用这个q_π改进这个策略π

Q-learning是off-policy，它的behavior policy是指导s_t怎么选择a_t；target policy是根据Q-learning计算得到q选择最大的，当q值逐渐收敛于最优的q值时，此时target policy也收敛于最优策略

8、A unified point of view

前面提到的TD算法其表达式可以统一；要解决的数学问题也可以统一

（1）介绍了这么多的TD算法，其实表达式是可以统一的

只有TD target不同，其中MC可以看作是特殊的n-step Sarsa，α_t设置为1即可

（2）要解决的数学问题也可以统一（E[]里面的就是TD target）

这些TD方法本质上是来求解给定策略的Bellman equation，将policy evolution和policy improvement相结合，让它可以搜索最优策略

9、Summary

value iteration和policy iteration是在有模型的情况下求解Bellman equation或Bellman optimality equation
TD learning是在没有模型的情况下求解Bellman equation或Bellman optimality equation

值函数近似

1、引出value function approximation的思想

value function approximation本身就具有很强的泛化能力，使用曲线拟合的例子引入值函数近似

（1）通过函数求出state value(v_π(s))的近似v_π(s,w)

直线形式：

二维曲线形式：

还可以继续增加曲线阶数，可以提高拟合程度但增加参数数量

拿函数去近似state value而不是用table去存储，优点是减少参数+增加泛化能力

2、值函数近似中目标函数的介绍

（1） 问题思想

拿v(s,w)去估计v_π(s)，当v(s,w)函数的结构确定时，我们就是调节w让v(s,w)逼近v_π(s)，找到最优的w。转换为—>给定策略π，找到近似函数v(s,w)尽可能去接近真实的state value

（2）公式

J(w)=E[(V_π(S)-v(S,w))²] （v()即为图片里的v^()，下面同理）

S的概率分布是什么？介绍两种：

1）uniform distribution：每个状态的概率都是一样的，为1/|S|

缺点是实际上所有的状态并不都是平等的，接近目标状态的那些状态更关键，希望这些状态权重大，从而使得它们的误差更小

2）stationary distribution： d_π(s)表示状态s的概率(权重)，是一个long-run的概率分布，是说达到平稳状态后agent访问到各个状态的概率

关于stationary distribution的细节：在定义objective function时，会出现stationary distribution

d_π(s)是状态转移概率矩阵P_π的特征向量，其特征值为1

3、目标函数的优化算法

有了目标函数就要对它优化，目的是最小化J(w)，使用gradient-descent算法

计算J(w)的梯度，这个梯度是需要计算random variable的expectation

实际上采用stochastic gradient代替true gradient，把随机变量S用采样s_t代替

v_π(s_t)是未知的，需要用别的量代替，一种是MC：用统计的g_t估计v_π(s_t)

还有一种是TD learning：用 TD target估计v_π(s_t)

伪代码：对每个episode中的每个(s_t，r_t+!，s_t+1)，用它去更新参数w，目的是找到最优w*

4、优化函数的选择

怎么去选择近似函数去估计v_π(s_t)呢？

（1）介绍两种方法

方法一，选择线性的函数，是相对于w的。重点是怎么选择feature vector,需要对问题有很深刻的理解，缺点是即使理解了也不好选择好的feature vector；优点是好分析理论性质

方法二，用神经网络逼近近似函数，是w的一个非线性函数。

（2）针对线性近似函数：可以计算出其梯度，梯度就是特征向量，代入原来的TD中，此时的TD算法叫做TD-Linear

tabular可以认为是linear function approximation的一种特殊情况

5、举例讲解

例子的基本情况：

先用基于model求出Ground truth，然后再将二维的表格三维化，生成三维坐标曲面，我们的近似函数对应的曲面应该和Ground truth的曲面越接近越好

每个episode出发的state-action-pair是随机选择的

实验前先看TD-Table的效果，还不错：

使用TD-Linear，首先建立feature vector

1）尝试1：

代入TD-Linear算法，得到估计的state value：效果很一般，证明需要更高阶数了

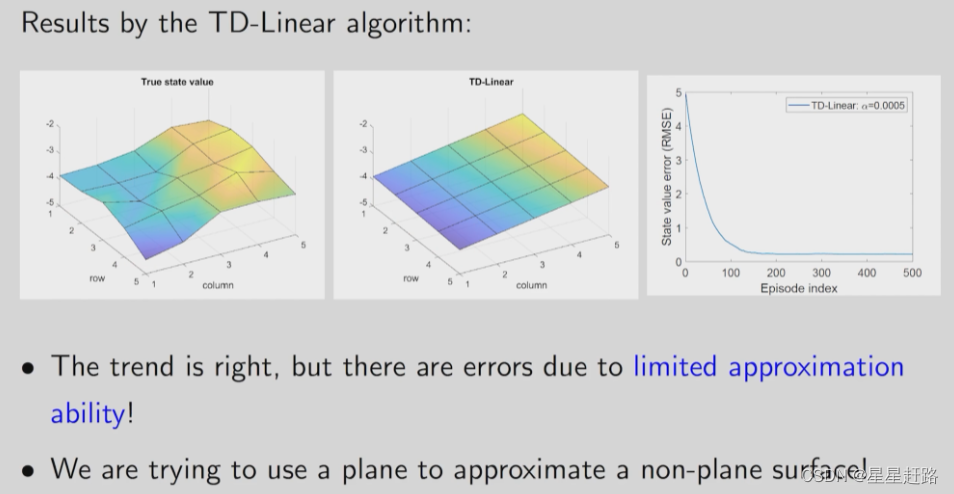
2）尝试2：把x，y的二阶放到feature vector中

结果：

3）尝试3：把x，y的三阶放到feature vector中

结果：

可以看出，更多的参数才能带来更好的结果，但不是意味着随着增加参数就能和tabular相近，因为线性函数结构已经固定了，故现在神经网络用的更广。

6、Summary

随机梯度取代目标函数的真实梯度，后用TD算法给出的估计值取代状态值，最后对特征值的估计值进行线性/神经网络估计近似替代

这段主要讲的是估计一个策略的state value的思想，后面在Sarsa是估计给定的策略π的action value；Q-learning和Deep Q-learning是估计optimal action value

7、Sarsa with function approximation

就是把用v(s,w)估计v_π(s)换成了用q(s,a,w)估计q_π(s,a)，还是在做policy evolution。

伪代码：（和tabular不同，tabular可以在table中索引找到q值；现在是把s_t、w_t+1、a代入到q^()中计算出q值)

8、Q-learning with function approximation

和Sarsa一模一样，只是TD target改变了

伪代码之on-policy：和Sarsa基本一样

9、Deep Q-learning：（神经网络引入强化学习）

Deep Q-learning也叫Deep Q-network，为了突出是Q-learning的变种，我们称之为Deep Q-learning。其中，神经网络扮演的角色是非线性模拟函数，去模拟q值

（1）刚刚介绍的Q-learning with function approximation公式(下面这个)

它属于理论上、偏底层的公式，用这个公式需要计算梯度、对参数进行修改，如果采用神经网络就只需要输入数据，神经网络能够选择合适的参数去做很好的训练(即一个黑盒，只需要去minimize损失函数就行)

（2）神经网络的loss function

（3）采用Gradient-descent优化loss function

参数w同时出现两次，不好求，可以把前面的w固定下来，记为w_T

基于此，在实际中也引入2个network，一个是一直更新的main network(这个网络是用来得到估计值q^(S,A,w))；一个是每过若干轮才更新target network(这个网络是用来得到估计的真实值R+γmax_a∈A(s·)q^(S`,a,w_T)， 即y^T)

当第一个参数w固定下来后，求∇_w就很容易了：

（4）Deep Q-learning的两个technique

1）Fixed Q-target：

使用两个结构一样，参数类似的网络。在数学上减少为了计算梯度的复杂度，会固定一个参数w^T然后去计算另一个参数w，所以需要两个网络来实现。实现过程：

2）Experience replay：

收集experience{(s,a,r,s`)}时是有顺序的，但是在使用的时候不必按顺序。把收集到的experience放到集合中，每次训练神经网络的时候从集合中取experience(取的时候要服从均匀分布)这样可以打破experience之间的correlation，而且可以多次运用到一些experience(因为是在replay buffet中均匀采样)

（5）Deep Q-learning伪代码

off-policy版本，不需要policy update因为不依赖policy去产生experience

期望值yT和估计值q^(s,a,w)间的距离是我们要优化的目标。

与原论文的算法不同的是，我们的输入是(s,a)，输出是q^(s,a)；
原文的输入是(s)，输出的是q^(s,a1)、
q^(s,a2)…、
q^(s,an)(n为动作个数)。原文的神经网络是更高效的，只需要输入一个s然后找出s对应的所有action value值，然后找最大值；而我们的神经网络需要输入好多次：

Deep Q-learning只需比较少的数据就可以得到不错的结果(因为value function approximation本身就有很强的泛化能力还采用了experience replay)而且还并不需要多深层的网络结构，这就是它的优点。