计数排序，认为是最简单的排序！

计数排序

由于用来计数的数组的长度取决于待排序数组中数据的范围，这使得计数排序对于数据范围很大的数组，需要大量时间和内存。计数排序不使用于含有非负数数组的排序。

计算排序思想

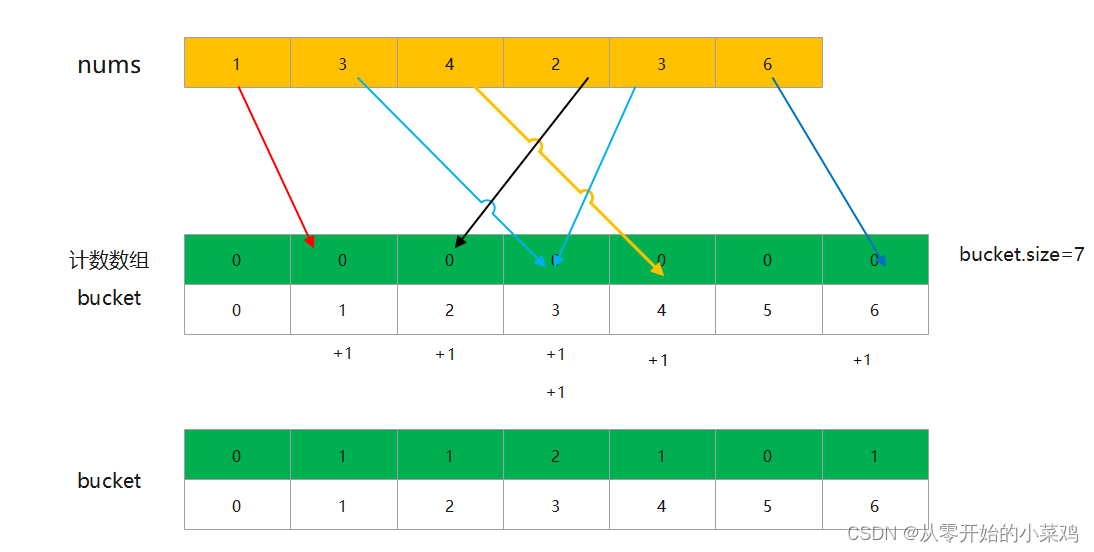
对数组{1，3，4，2，3，6}进行计数排序

计数排序步骤：

1. 找到数组中的最大值

代码如下

	int maxVal=0;
    //找到数组中的最大值
    for(int i:nums){
        maxVal=i>maxVal?i:maxVal;
    }

2. 申请计数数组的长度:原数组中最大值+1

计数数组元素初始化为0
原数组的最大值为6，那么申请计数数组的长度为7，并初始化为0

代码如下：

	vector<int> bucket(maxVal+1,0);

3. 为计数数组赋值。

统计数组中每个值为i的元素出现的次数，存入计数数组下标为i的位置.
在此例中：
数组中值为1出现了一次，存入bucket数组下标为1的位置。即bucket[1]=1.
数组中值为3出现了两次，存入bucket数组下标为3的位置。即bucket[3]=2.
数组中值为4出现了一次，存入bucket数组下标为4的位置。即bucket[4]=1.
数组中值为2出现了一次，存入bucket数组下标为2的位置。即bucket[2]=1.
数组中值为6出现了一次，存入bucket数组下标为6的位置。即bucket[6]=1.

代码如下：

	for(int i=0;i<nums.size();i++){
		++bucket[nums[i]];
	}

4. 反向填充到原数组

计数数组的下标对应原数组中的值
计数数组中的值对应原数组中值的个数
计数数组中的值还原到原数组的值，将计数数组计数不为0的下标值存入原数组中，每存入一次，该下标对应的计数数组中的计数减一。

原数组没有在bucket数组中计数为0的下标值(判断条件）

因此在还原时，如果bucket数组中的值不为0，则将此值的下标放到原数组中，再将bucket数组的值减一，即计数减一。

代码如下

int index=0;
for(int i=0;i<bucket.size();i++){
	while(bucket[i]!=0){
		nums[index++]=i;
		bucket[i]--;
	}
}

完整代码

计数排序完整代码如下

#include <iostream>
#include <vector>
using namespace std;
void countSort(vector<int> &nums) {
 //1.找到数组中的最大值
 int maxValue=0;
 for(auto i:nums){
   maxValue=maxValue>i?maxValue:i;
 }
 //2.初始化计数数组
 vector<int> bucket(maxValue+1,0);
 //3.为计数数组赋值
 for(int i=0;i<nums.size();i++){
     bucket[nums[i]]++;
 }
 //4.还原到原数组中
 maxValue=0;
 for(int i=0;i<bucket.size();i++){
   while(bucket[i]!=0){
     nums[maxValue++]=i;
     bucket[i]--;
   }
 }
}
int main() {
 vector<int> nums = {2, 4, 7, 8, 3, 4};
 countSort(nums);
 for (auto i : nums) {
   cout << i << " ";
 }
}


}

时间复杂度和空间复杂度

• 时间复杂度：O(n+k)
• 空间复杂度：O(n+k)