本文深入探讨了二叉搜索树的性质及其在数据结构中的应用，特别是Treap作为一种弱平衡的二叉搜索树。介绍了Treap的分裂(split)和合并(merge)操作，以及它们如何确保树的平衡。此外，文章还详细解释了无旋Treap和旋转Treap的插入、删除操作，展示了如何通过旋转或分裂保持树的平衡。
前言：
文章篇幅较大，初学者建议耐心看完。
二叉搜索树的性质： 若它的左子树不空，则左子树上所有结点的值均小于它的根节点的值； 若它的右子树不空，则右子树上所有结点的值均大于它的根结点的值；二叉搜索树对于一个随机序列的最优复杂度是 O ( l o g n ) O(logn) O(logn)，对于一个有序序列复杂度会被卡成 O ( n ) O(n) O(n)。
T r e a p Treap Treap 是一种 弱平衡 的 二叉搜索树。它的数据结构由二叉树和二叉堆组合形成，名字也因此为 t r e e tree tree 和 h e a p heap heap 的组合。
T r e a p Treap Treap 的每个结点上除了按照二叉搜索树排序的 k e y key key 值外要额外储存一个叫 p r i o r i t y priority priority 的值。它由每个结点建立时随机生成，并按照 最大堆 性质排序。因此 t r e a p treap treap 除了要满足二叉搜索树的性质之外，还需满足父节点的 p r i o r i t y priority priority 大于等于两个子节点的值。所以它是 期望平衡 的。搜索，插入和删除操作的期望时间复杂度为 O ( l o g n ) O(logn) O(logn) 。
以上信息来自网络。
约定：上文中的key和priority下文分别用数值(val)和权重(wgt)称呼
无旋Treap（范浩强Treap）
无旋 T r e a p Treap Treap 又称为分裂 T r e a p Treap Treap , 其核心操作为 分裂(split) 和 合并(merge) 两种操作。
分裂操作接受两个参数，第一个参数为当前 T r e a p Treap Treap 的根节点，第二个为一个数值 v a l u e value value，该操作会将 T r e a p Treap Treap 分裂成两棵树，第一棵树为数值小于等于 v a l val val 的树，第二棵树为数值大于 v a l val val 的树。操作返回分裂后两棵树的根节点。
现在假设我们要将根为 root 的 Treap 分裂成值小于等于7和值大于7的两棵树。效果如图所示。
代码：
// 以p为根节点 按值v分裂
// 返回两棵树
// first -- 值小于等于 v
// second -- 值大于 v
PII split(int p, int v)
{
if (!p) return { 0, 0 };
if (val[p] <= v) // 左子树全部小于等于v 右子树有部分小于v 递归右子树
{
// 将右子树与根p分裂
// 将右子树中值小于等于v的子树挂在p的右子树
// 因为p的右子树的值全都大于p的左子树和p的值
// 所以把右子树中值小于等于v的子树挂在p的右子树不会破坏二叉搜索树的性质
// 这样操作的正确性是显然的
PII ret = split(r[p], v);
r[p] = ret.first;
update(p);
return { p, ret.second };
}
else // 左子树有部分小于等于v 递归左子树
{
// 这里的操作与上面相反
PII ret = split(l[p], v);
l[p] = ret.second;
update(p);
return { ret.first, p };
}
}
合并操作同样接受两个参数且分别为两棵树的根节点，并且第一棵树的数值 v a l val val 全部都要小于第二棵树的数值 v a l val val，这样做的意义我们稍后讨论。该操作将会把两棵树合并为一棵树并返回合并后的根节点。
在上面分裂出的两棵树基础上我们给他加入权值 ( w g t ) (wgt) (wgt)，这样做的原因是我们在对它进行合并操作是用权值来按照大根堆(小根堆)的性质进行合并。下面我们以大根堆为例。
不难发现经过分裂操作得到的两棵树 u , v u,v u,v, u u u 的数值全部小于 v v v,且两棵树都满足二叉搜索树的性质。所有合并时我们考虑在权值满足大根堆的性质的同时如何不去破坏它二叉搜索树的性质。
让我们来看图说话：数值为
6
6
6 的节点
u
u
u 和数值为
10
10
10 的节点
v
v
v它们的权值分别为
17
17
17 和
15
15
15，按照大根堆的性质
u
u
u 要作为
v
v
v 的根节点，也就是说
v
v
v 要作为
u
u
u 子树，也无非就是作为左子树或右子树两种选择，但因为我们要保证合并后的树也是二叉搜索树，并且
u
u
u 的权值全都小于
v
v
v 的权值，所以我们把
v
v
v 作为
u
u
u 的右子树，以此来保证合并后的树也是一棵二叉搜索树。但是
u
u
u 的右子树
r
[
u
]
r[u]
r[u] 并不为空，我们又去合并
r
[
u
]
r[u]
r[u] 和
v
v
v。这样递归的操作直到合并完成为止。效果如图。
代码：
int merge(int u, int v) // u的val全部小于v的val
{
// 小技巧 当有一棵树为空时返回另一棵树
if (!u || !v) return u + v;
else if (wgt[u] > wgt[v])
{
// u的权值大于v的权值 大根堆v应该在u的下面 且 v.val > u.val 所以 v应该挂在u的右子树
r[u] = merge(r[u], v); // u的右子树可能不为空 先合并u的右子树和v
update(u);
return u; // u 挂着 v 根为 u
}
else
{
// u的权值小于等于v的权值 u应该挂在v的下面 且 v.val > u.val 所以 u应该挂在v的左子树
l[v] = merge(u, l[v]); // v的左子树可能不为空 先合并u 和 v的左子树
update(v);
return v; // v 挂着 u 根为 v
}
}
建议读者仔细理解代码中**挂着**的含义，对Treap的学习至关重要。
那么无旋
t
r
e
a
p
treap
treap 如何保持平衡呢。
不难发现分裂和合并操作就是无旋
T
r
e
a
p
Treap
Treap 保持平衡的核心。
下面我们来学习插入(insert) 操作。
插入操作，接受一个参数,为数值
v
v
v, 下面讲解可重集合的插入方法。
1、将
T
r
e
a
p
Treap
Treap 按数值
v
v
v 分裂成两棵树
2、用数值
v
v
v 新建一个节点
3、先合并第一棵树与新节点
4、将合并后的树与第二棵树合并
这里我们发现每次的插入操作都会将原树分裂然后合并，因为合并时我们是用权值按堆的性质合并，并且权值是随机的，因此每次插入操作也就完成了树的平衡。
代码：
inline int creat_Node(int v) // 创建一个新节点并返回它的根
{
val[++idx] = v, wgt[idx] = rand();
size[idx] = 1;
return idx;
}
void insert_(int v)
{
// 按值分裂成两棵树
// 将新建的节点与其中一课数先合并，再把剩下的两棵树合并
PII ret = split(root, v);
root = merge(merge(ret.first, creat_Node(v)), ret.second);
}
最后我们来学习删除(erase) 操作。
删除操作接受一个参数，其为数值
v
v
v，下面讲解可重集合的删除操作。
1、将原树按数值
v
v
v 分裂成两棵树，用
p
1
p1
p1 接收返回值
2、将
p
1.
f
i
r
s
t
p1.first
p1.first 按数值
v
−
1
v-1
v−1 分裂成两棵树，用
p
2
p2
p2 接收返回值
3、此时
p
2.
s
e
c
o
n
d
p2.second
p2.second 为数值全为
v
v
v 的树，我们合并它的左右子树并用
q
q
q 接收返回值
4、先合并
p
2.
f
i
r
s
t
p2.first
p2.first 和
q
q
q,用
p
p
p 来接收返回值
5、最后合并
p
p
p 和
p
1.
s
e
c
o
n
d
p1.second
p1.second
不难发现，删除操作通过两次分裂操作来孤立数值为 v v v 的点，然后抛弃孤立点，合并其它的树来完成。
核心操作讲解完毕，下面给出洛谷 P3369 【模板】普通平衡树 AC代码。
数据结构已经封装完毕。
#include <bits/stdc++.h>
using namespace std;
class treap
{
private:
typedef pair<int, int> PII;
static const int N = 100010;
int val[N], wgt[N], l[N], r[N], size[N]; // 数值 权重 左子树 右子树 当前树的大小
int idx, root; // 当前开到第几个 根节点
int INF = 0x3f3f3f3f;
inline int creat_Node(int v) // 创建一个新节点并返回它的根
{
val[++idx] = v, wgt[idx] = rand();
size[idx] = 1;
return idx;
}
// 更新节点的size
inline void update(int p) { size[p] = size[l[p]] + size[r[p]] + 1; }
// 以p为根节点 按值v分裂
// 返回两棵树
// first -- 小于等于 v
// second -- 大于 v
PII split(int p, int v)
{
if (!p) return { 0, 0 };
if (val[p] <= v) // 左子树全部小于等于v 右子树有部分小于v 递归右子树
{
PII ret = split(r[p], v);
r[p] = ret.first;
update(p);
return { p, ret.second };
}
else // 左子树有部分小于等于v 递归左子树
{
PII ret = split(l[p], v);
l[p] = ret.second;
update(p);
return { ret.first, p };
}
}
int merge(int u, int v) // u的val全部小于v的val
{
if (!u || !v) return u + v;
else if (wgt[u] > wgt[v])
{
// u的权值大于v的权值 大根堆v应该在u的下面 且 v.val > u.val 所以 v应该挂在u的右子树
r[u] = merge(r[u], v); // u的右子树可能不为空 先合并u的右子树和v
update(u);
return u; // u 挂着 v 更为 u
}
else
{
// u的权值小于等于v的权值 u应该挂在v的下面 且 v.val > u.val 所以 u应该挂在v的左子树
l[v] = merge(u, l[v]); // v的左子树可能不为空 先合并u 和 v的左子树
update(v);
return v; // v 挂着 u 跟为 v
}
}
int find(int v)
{
int p = root;
while (p)
{
if (val[p] == v) return p;
else if (val[p] > v) p = l[p];
else p = r[p];
}
return -INF; // 没找到返回一个不存在的数
}
void insert_(int v)
{
// 按值分裂成两棵树
// 将新建的节点与其中一课数先合并，再把剩下的两棵树合并
PII ret = split(root, v);
root = merge(merge(ret.first, creat_Node(v)), ret.second);
}
void erase_(int v)
{
// 先用分裂操作将目标点孤立
// 合并目标点的左右子树
// 最后将除目标点外全部合并
PII ret = split(root, v);
PII p = split(ret.first, v - 1);
int q = merge(l[p.second], r[p.second]);
root = merge(merge(p.first, q), ret.second);
}
int rank_Of_Val(int p, int v) // 值的排名
{
PII ret = split(root, v - 1);
int rank = size[ret.first] + 1;
root = merge(ret.first, ret.second);
return rank;
}
int val_Of_Rank(int p, int rank) // 排名的值
{
if (!p) return INF;
if (size[l[p]] >= rank) return val_Of_Rank(l[p], rank);
else if (size[l[p]] + 1 >= rank) return val[p];
else return val_Of_Rank(r[p], rank - size[l[p]] - 1);
}
int pre(int p, int v) // 前驱
{
if (!p) return -INF;
if (val[p] >= v) return pre(l[p], v);
else return max(val[p], pre(r[p], v));
}
int next(int p, int v) // 后继
{
if (!p) return INF;
if (val[p] <= v) return next(r[p], v);
else return min(val[p], next(l[p], v));
}
void print(int p) // 中序遍历
{
if (l[p]) print(l[p]);
cout << val[p] << " " << wgt[p] << endl;
if (r[p]) print(r[p]);
}
public:
void insert(int v) { insert_(v); }
void erase(int v) { erase_(v); }
int rank_Of_Val(int v) { return rank_Of_Val(root, v); }
int val_Of_Rank(int v) { return val_Of_Rank(root, v); }
int pre(int v) { return pre(root, v); }
int next(int v) { return next(root, v); }
void print() { print(root); }
};
treap t;
int n;
int main()
{
cin >> n;
while (n--)
{
int op, v;
scanf("%d%d", &op, &v);
if (op == 1) t.insert(v);
else if (op == 2) t.erase(v);
else if (op == 3) printf("%d\n", t.rank_Of_Val(v));
else if (op == 4) printf("%d\n", t.val_Of_Rank(v));
else if (op == 5) printf("%d\n", t.pre(v));
else printf("%d\n", t.next(v));
}
return 0;
}
旋转Treap
与无旋 T r e a p Treap Treap 不同的是，旋转 T r e a p Treap Treap 保持了平衡的方式是通过旋转（听君一席话qwq）,旋转分为 左旋 和 右旋。即在满足二叉搜索树的条件下根据堆的优先级对 t r e a p treap treap 进行平衡操作。接下来我们来学习它的核心操作。
左旋： 当右子树 r [ p ] r[p] r[p] 的权值大于根 p p p 的权值就左旋，把右子树旋转为 p p p 根，根旋转为 r [ p ] r[p] r[p] 左子树，而 r [ p ] r[p] r[p] 原来的左子树作为 p p p 的右子树。
p
p
p 作为
r
[
p
]
r[p]
r[p] 的左子树的原因是：
p
p
p 及
l
[
p
]
l[p]
l[p] 的数值全都小于
r
[
p
]
r[p]
r[p] ,为了旋转保持堆性质的同时不改变二叉搜索树的性质才这样做。效果如图。
代码：
inline void zag(int &p) // 左旋 p.r.wgt > p.wgt p要挂在p.r的左子树
{
int q = r[p];
r[p] = l[q], l[q] = p, p = q;
update(l[p]), update(p);
}
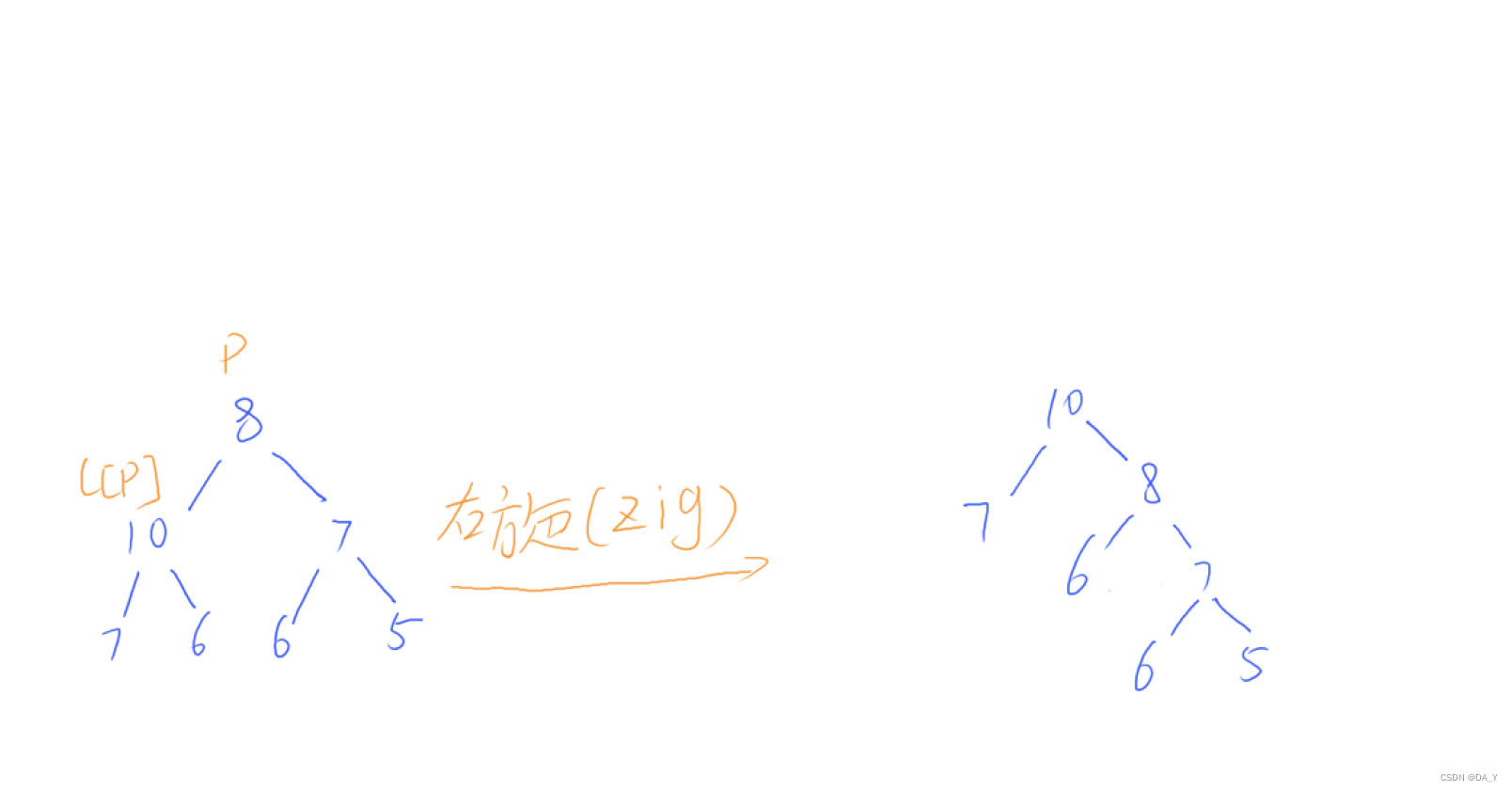
右旋： 当左子树
l
[
p
]
l[p]
l[p] 的权值大于根
p
p
p 的权值时右旋。
将
l
[
p
]
l[p]
l[p] 旋转为
p
p
p 的根，
p
p
p 旋转为
r
[
p
]
r[p]
r[p] 的右子树，再把
l
[
p
]
l[p]
l[p] 的右子树挂在
p
p
p 的左子树上。效果如图。
代码：
inline void zig(int &p) // 右旋 p.l.wgt > p.wgt p要挂在p.l的右子树
{
int q = l[p];
l[p] = r[q], r[q] = p, p = q;
update(r[p]), update(p);
}
可以得出左旋和右旋为镜像操作，从代码上也不难看出。
插入操作：旋转 T r e a p Treap Treap 能够维持平衡的原因是在 插入(insert) 时按二叉搜索树的性质插入，同时又按堆的性质进行旋转。
代码：
void insert(int &p, int v)
{
if (!p) p = creat_Node(v); // 创建一个新点节点
else if (val[p] == v) cnt[p] ++; // 如果该值存在 该值数量加1
else if (val[p] > v) // 按二叉搜索树的性质 插到p左子树
{
insert(l[p], v);
// 判读是否需要旋转
if (wgt[l[p]] > wgt[p]) zig(p);
}
else // 同理 插到p的右子树
{
insert(r[p], v);
if (wgt[r[p]] > wgt[p]) zag(p);
}
update(p);
}
删除操作：在对旋转 t r e a p treap treap 做删除操作时，遵循堆的删除操作。通过将要删除的点与权值较小的子节点不断旋转交换，直到要删除的点变为叶节点。
代码：
// 在对旋转 treap 做删除操作时，遵循堆的删除操作。
// 通过将要删除的点与优先级较小的子节点不断旋转交换，直到要删除的点变为叶节点
void erase(int &p, int v) //
{
if (!p) return; // 没有找到该值
if (val[p] == v)
{
// 找到该值v并且它的个数大于1时，将其数量减1就行
if (cnt[p] > 1) { cnt[p]--; }
else if (l[p] || r[p]) // 值不是叶子节点
{
// 通过左右旋转把该节点旋转到叶子节点
// 判断应该左旋还是右旋
if (!r[p] || wgt[l[p]] > wgt[r[p]])
{
zig(p);
erase(r[p], v);
}
else
{
zag(p);
erase(l[p], v);
}
}
else { p = 0; } // 删除节点 0是空节点
}
// 按照二叉搜索树的性质查找v
else if (val[p] > v) erase(l[p], v);
else erase(r[p], v);
update(p);
}
核心操作讲解完毕。
下面同样给出洛谷 P3369 【模板】普通平衡树 AC代码。
数据结构已封装完毕。
#include <bits/stdc++.h>
using namespace std;
class treap
{
private:
static const int N = 100010;
int val[N], wgt[N], l[N], r[N], size[N], cnt[N]; // 数值 权重 左子树 右子树 当前树的大小 当数的个数
int idx, root; // 当前开到第几个 根节点
int INF = 0x3f3f3f3f;
inline void update(int p) { size[p] = size[l[p]] + size[r[p]] + cnt[p]; }
inline void zig(int &p) // 右旋 p.l.wgt > p.wgt p要挂在p.l的右子树
{
int q = l[p];
l[p] = r[q], r[q] = p, p = q;
update(r[p]), update(p);
}
inline void zag(int &p) // 左旋 p.r.wgt > p.wgt p要挂在p.r的左子树
{
int q = r[p];
r[p] = l[q], l[q] = p, p = q;
update(l[p]), update(p);
}
inline int creat_Node(int v)
{
val[++idx] = v, wgt[idx] = rand();
cnt[idx] = size[idx] = 1;
return idx;
}
void insert(int &p, int v)
{
if (!p) p = creat_Node(v);
else if (val[p] == v) cnt[p] ++;
else if (val[p] > v) // 按二叉搜索树的性质 插到p左子树
{
insert(l[p], v);
if (wgt[l[p]] > wgt[p]) zig(p);
}
else // 同理 插到p的右子树
{
insert(r[p], v);
if (wgt[r[p]] > wgt[p]) zag(p);
}
update(p);
}
// 在对旋转 treap 做删除操作时，遵循堆的删除操作。
// 通过将要删除的点与优先级较小的子节点不断旋转交换，直到要删除的点变为叶节点
void erase(int &p, int v) //
{
if (!p) return; // 没有找到该值
if (val[p] == v)
{
// 找到该值v并且它的个数大于1时，将其数量减1就行
if (cnt[p] > 1) { cnt[p]--; }
else if (l[p] || r[p]) // 值不是叶子节点
{
// 通过左右旋转把该节点旋转到叶子节点
// 判断应该左旋还是右旋
if (!r[p] || wgt[l[p]] > wgt[r[p]])
{
zig(p);
erase(r[p], v);
}
else
{
zag(p);
erase(l[p], v);
}
}
else { p = 0; } // 删除节点 0是空节点
}
// 按照二叉搜索树的性质查找v
else if (val[p] > v) erase(l[p], v);
else erase(r[p], v);
update(p);
}
int rank_Of_Val(int p, int v) // 值的排名
{
if (!p) return 0;
if (val[p] == v) return size[l[p]] + 1;
else if (val[p] > v) return rank_Of_Val(l[p], v);
else return size[l[p]] + cnt[p] + rank_Of_Val(r[p], v);
}
int val_Of_Rank(int p, int rank) // 排名的值
{
if (!p) return INF;
if (size[l[p]] >= rank) return val_Of_Rank(l[p], rank);
else if (size[l[p]] + cnt[p] >= rank) return val[p];
else return val_Of_Rank(r[p], rank - size[l[p]] - cnt[p]);
}
int pre(int p, int v) // 值的前驱
{
if (!p) return -INF;
if (val[p] >= v) return pre(l[p], v);
else return max(val[p], pre(r[p], v));
}
int next(int p, int v)
{
if (!p) return INF;
if (val[p] <= v) return next(r[p], v);
else return min(val[p], next(l[p], v));
}
public:
void insert(int v) { insert(root, v); }
void erase(int v) { erase(root, v); }
int rank_Of_Val(int v) { return rank_Of_Val(root, v); }
int val_Of_Rank(int rank) { return val_Of_Rank(root, rank); }
int pre(int v) { return pre(root, v); }
int next(int v) { return next(root, v); }
};
treap t;
int n;
int main()
{
cin >> n;
while (n--)
{
int op, v;
scanf("%d%d", &op, &v);
if (op == 1) t.insert(v);
else if (op == 2) t.erase(v);
else if (op == 3) printf("%d\n", t.rank_Of_Val(v));
else if (op == 4) printf("%d\n", t.val_Of_Rank(v));
else if (op == 5) printf("%d\n", t.pre(v));
else printf("%d\n", t.next(v));
}
return 0;
}
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
