java汉诺塔（含汉诺塔问题的详解）

最新推荐文章于 2023-08-19 20:21:59 发布

原创最新推荐文章于 2023-08-19 20:21:59 发布 · 2.4k 阅读

20 ·

CC 4.0 BY-SA版权

文章标签：

#java #数据结构 #算法 #汉诺塔

这篇文章详细介绍了汉诺塔问题的起源、解决思路，通过逐步图示展示了如何进行递归操作，并提供了Java代码实例。核心在于理解递归策略和小盘子优先的移动原则。

一：汉诺塔问题

汉诺塔问题是一个经典的问题。汉诺塔（Hanoi Tower），又称河内塔，源于印度一个古老传说。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，任何时候，在小圆盘上都不能放大圆盘，且在三根柱子之间一次只能移动一个圆盘。问应该如何操作？（每次只能移动1个盘子，大盘子只能放在小盘子下面）

二：汉诺塔问题思路

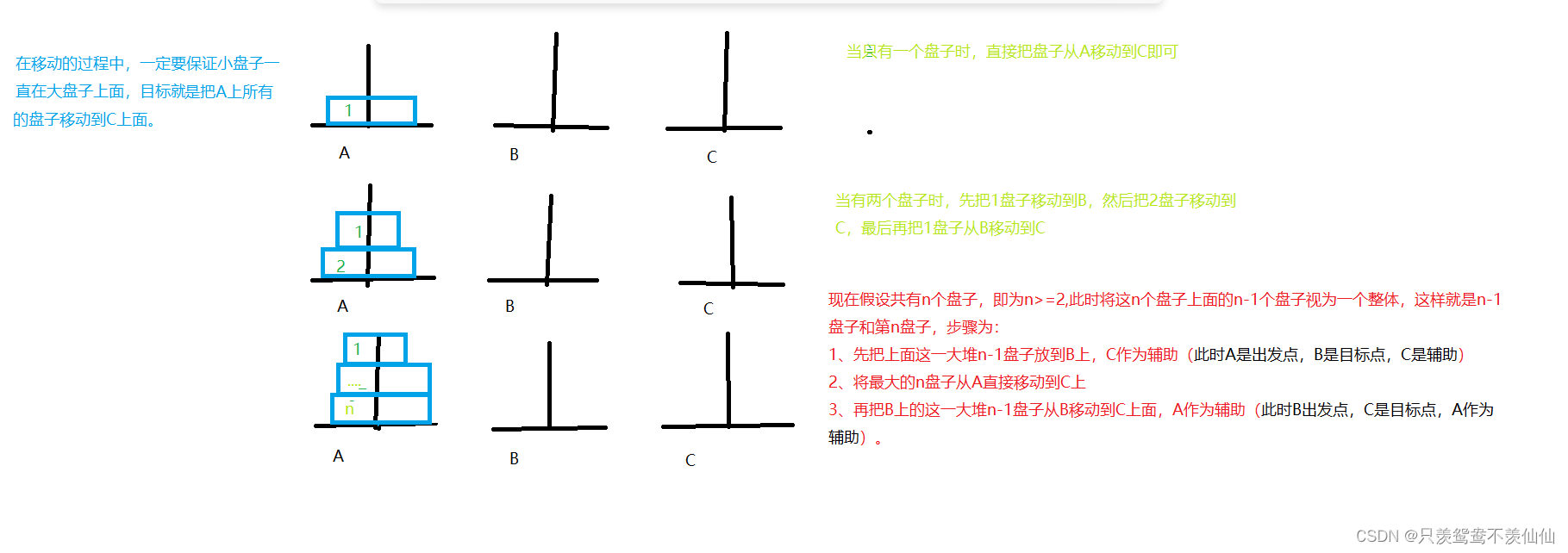三：图示化思路

1、汉诺塔一个盘子

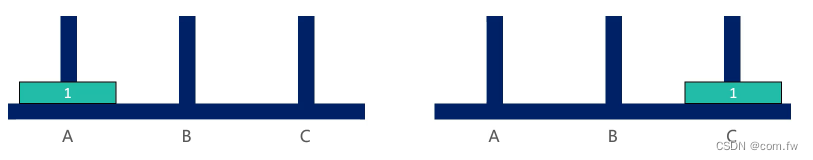
2、汉诺塔两个盘子

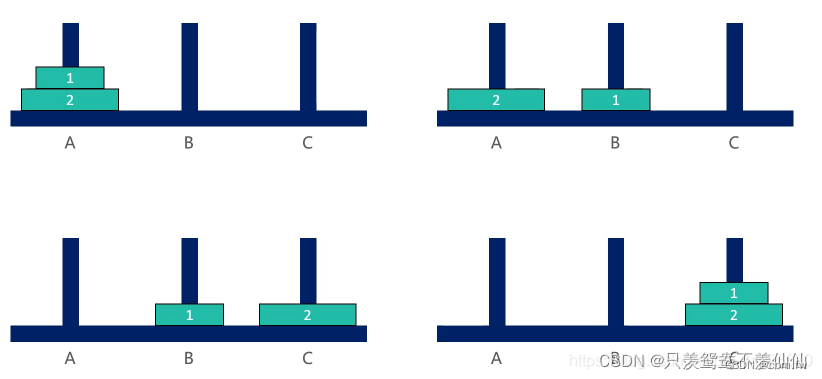
3、汉诺塔三个盘子

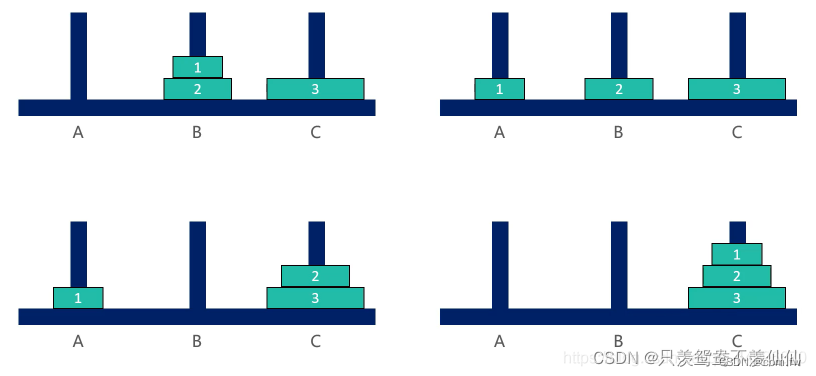
4、想法
（1）当 n == 1时，直接将盘子从 A 移动到C
（2）当 n > 1时，可以拆分成3大步骤
①将 n– 1 个盘子从 A 移动到B

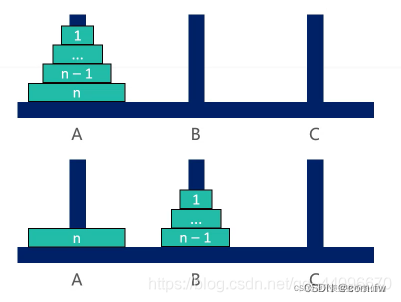
②将编号为 n 的盘子从 A 移动到C

③将 n– 1 个盘子从 B 移动到C

在此过程中，步骤①③ 明显是个递归调用

四：代码展示

package hanoitower;

public class HanoiTower {

	public static void main(String[] args) {
		// TODO Auto-generated method stub
		hanoiTower(3,'A','B','C');

	}
	public static void hanoiTower(int num, char a, char b, char c) {
		if(num == 1) {
			System.out.println("第" + num + "个盘" + "从" + a + "移动到" + c);
		}else {
			hanoiTower(num - 1, a, c ,b);
			System.out.println("第" + num + "个盘" + "从" + a + "移动到" + c);
			hanoiTower(num - 1, b, a, c);
		}
		
	}

}