文章目录
88. 合并两个有序数组
非递减顺序 排列的整数数组 nums1 和 nums2,另有两个整数 m 和 n ,分别表示 nums1 和 nums2 中的元素数目。合并 nums2 到 nums1 中,使合并后的数组同样按 非递减顺序 排列。合并后数组不应由函数返回,而是存储在数组 nums1 中。为了应对这种情况,nums1 的初始长度为 m + n,其中前 m 个元素表示应合并的元素,后 n 个元素为 0 ,应忽略。nums2 的长度为 n 。输入:nums1 = [1,2,3,0,0,0], m = 3, nums2 = [2,5,6], n = 3输出:[1,2,2,3,5,6]
void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n){
int* temp = (int*)malloc((m + n)*sizeof(int));
if (temp == NULL){
return;
}
int i = 0, j = 0, index = 0;
while (i < m && j < n)
{
if (nums1[i] <= nums2[j]){
temp[index++] = nums1[i++];
}
else{
temp[index++] = nums2[j++];
}
}
while (i < m){
temp[index++] = nums1[i++];
}
while (j < n){
temp[index++] = nums2[j++];
}
memcpy(nums1, temp, (m + n)*sizeof(int));
}
//方法2:
void merge(int* nums1, int nums1size, int m, int* nums2, int nums2size, int n){
{ int end1 = m - 1, end2 = n - 1, index = m + n - 1;
while (end1 >= 0 && end2 >= 0)
{
if (nums2[end2] >= nums1[end1]){
nums1[index--] = nums2[end2--];
}
else{
nums1[index--] = nums1[end1--];
}
}
while (end2 >= 0){
nums1[index--] = nums2[end2--]; }
}
}
找出那个缺失的整数
数组nums包含从0到n的所有整数,缺了一个。找出那个缺失的整数。O(n)时间内完成,输入:[3,0,1],输出:2
int missingNumber(int* nums, int numsSize){
int sum = ( 1+numsSize)*numsSize/2;
//数组中所有元素求和
int arraySum = nums[0];
for(int i = 1; i < numsSize; ++i){
arraySum += nums[i];
}
//做差
return sum-arraySum;
}
线性表=有n个元素构成的集合,逻辑结构呈现线性。
如果是双向链表,哪边是栈顶,哪边是栈底都可以,入栈=头插、出数据=头删;实现栈建议用数组
189. 轮转数组
数组中的元素向右轮转 k 个位置,入: nums = [1,2,3,4,5,6,7], k = 3
输出: [5,6,7,1,2,3,4]解释:
向右轮转 1 步: [7,1,2,3,4,5,6]
向右轮转 2 步: [6,7,1,2,3,4,5]
向右轮转 3 步: [5,6,7,1,2,3,4]
void rotate(int*nums,int numssize,int k){
k %= numssize;
//控制:移动k轮
for(int i = 0; i < k; ++i)
{
// 1.先将最后一个元素=numssize-1保存起来
int last = nums [ numssize-1];
// 2.从后往前将0~numssize-2往后移动一个位置
for(int j = numssize-2; j >= 0; --j)
{
nums[j+1] = nums[j];
}
nums[0] = last;
}
}//方法1=时间复杂度=k*numssize
//方法2:
//1.先将前size-k:4个元素逆置:4 3 2 1 5 6 7,⒉将后k个元素逆置:4 3 2 1 7 6 5,3.对数据整体逆置:5 6 7 1 2 3 4,前2步加起来复杂度=O(N),最后1步复杂度=O(N),最终=O(N)
void reverse(int*array , int left, int right){
while(left < right){
int temp = array[left];
array[left] = array[right];
array[right] = temp;
left++;
right--; }
}
void rotate( int*nums, int numssize,int k)
{
k %= numssize;//有3个数据,移动4次=移动1次效果
reverse( nums, 0,numssize-k-1);
reverse(nums, numssize-k,numssize-1);
reverse( nums, 0,numssize-1);
}
26.原地删除重复出现的元素
添加链接描述
开始【1,1,2,2,2,3,4】结果:1234
中间
结束
int removeDuplicates(int* nums, int numsSize){
if (numsSize == 0)return 0;//极端情况:数组里没有数字时
int prev = 0, cur = 1, dst = 0;
while (cur < numsSize){
if (nums[prev] != nums[cur]){
nums[dst] = nums[prev];
prev++; cur++; dst++;//前置++是先自加,后使用
}
else{ ++prev; ++cur; }
}nums[dst] = nums[prev];
dst++; prev++; return dst;}
989.数组形式的整数加法
int* addtoarrayform(int* A, int Asize,int k,int*returnsize){
int ksize = 0, knum = k;//nextnum=进位、ksize=k有几位数
while (knum){
++ksize; knum /= 10;
}int len = Asize > ksize ? Asize : ksize;//A(4位数)和k(2位数)比较位数,取位数大的(开辟5位数的空间retarr)
int* retarr = (int*)malloc(sizeof(int)*(len + 1));
int Ai = Asize - 1;//数组A的下标,从个位开始
int reti = 0; int nextnum = 0;
while (len--){
int a = 0; //设a的原因:A=2位数,k=4位数时
if (Ai >= 0)
{
a = A[Ai]; Ai--;
}int ret = a + k % 10 + nextnum;//A+k的单次计算结果=ret
k /= 10;
if (ret > 9)
{
ret -= 10; nextnum = 1;
}
else{ nextnum = 0; }retarr[reti] = ret;//retarr(最终计算结果)
++reti;
int left = 0, right = reti - 1; //retarr里的数字逆置
while (left < right){
int tem = retarr[left];
retarr[left] = retarr[right];
retarr[right] = temp;
++left; --right;
}*returnsize = reti; //*returnsize=scanf输出型参数=传变量的地址,printf输入型参数
return retarr;}
}
排序子序列
#include<iostream>
#include<vector>
using namespace std;
int main() {
int n;
cin >> n;
vector<int> a;
a.resize(n + 1);//若有6个数,开7个空间,
a[n] = 0; int i = 0;
for (i = 0; i < n; ++i)
cin >> a[i];
i = 0;
int count = 0;
while (i < n)
{ // 非递减子序列 如:1223
if (a[i] < a[i + 1])
{ //i=5时,5<6&&a[5] <= a[6],a[6]=0
while (i < n && a[i] <= a[i + 1])
i++; count++; i++;
}else if
(a[i] == a[i + 1])
{ i++;
}
else // 非递增子序列
{
while (i < n && a[i] >= a[i + 1])
i++;
count++;
i++;
}
}
cout << count << endl;
return 0;
}
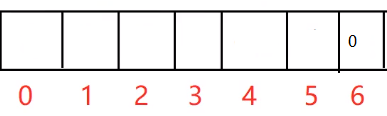
DD1 连续最大和
添加链接描述
动规问题
#include <iostream>
#include<vector>
using namespace std;
int GetMax(int a, int b) //得到两个数的最大值
{ return (a) > (b) ? (a) : (b); }
int main()
{ int size;
cin >> size;
vector<int> nums(size);
for (size_t i = 0; i < size; ++i)
cin >> nums[i];
int Sum = nums[0]; //临时最大值
int MAX = nums[0]; //比较之后的最大值
for (int i = 1; i < size; i++)
{
Sum = GetMax(Sum + nums[i], nums[i]); //状态方程
if (Sum >= MAX)
MAX = Sum;
}
cout << MAX << endl;
return 0;
}

45840-不要二
((x1-x2)*(x1-x2)+(y1-y2)* (y1-y2)) == 4
有这几种情况:1+3=4;3+1=4;2+2=4;0+4=4;4+0=4,但只有后2种符合现实,
(×1-x2)*(x1-x2)=0 x1==x2 y1-y2=2 y1=y2+2
(y1-y2) * (y1-y2)=0 y1=y2 x1-x2=2 x1 = x2+2
[i][j]位置放了蛋糕,[i+2][j]和[i][j+2]的位置就不可以放蛋糕
防止[i+2]和[j+2]越界
#include<iostream>
#include<vector>
using namespace std;
int main() {
int w,h,res = 0;
cin >> w >> h;
vector<vector<int>> a;
a.resize(w);
for(auto& e : a)
e.resize(h, 1);
for(int i=0;i<w;i++)
{
for(int j=0;j<h;j++)
{
if(a[i][j]==1)
{
res++; // 标记不能放蛋糕的位置
if((i+2)<w)
a[i+2][j] = 0;
if((j+2)<h)
a[i][j+2] = 0;
}
}
}
cout << res;
return 0;
}
23271-数组中出现次数超过一半的数字
int MoreThanHalfNum_Solution(vector<int> numbers)
{// 因为用到了sort,时间复杂度O(NlogN),并非最优
if(numbers.empty())
return 0;
sort(numbers.begin(),numbers.end()); // 排序,取数组中间那个数
int middle = numbers[numbers.size()/2];
int count=0; // 出现次数
for(int i=0;i<numbers.size();++i)
{再次遍历这个数组,看一下middle出现了多少次
if(numbers[i]==middle)
++count;
}
return (count>numbers.size()/2) ? middle : 0;
}
众数:就是出现次数超过数组长度一半的那个数字如果两个数不相等,就消去这两个数,最坏情况下,每次消去一个众数和一个非众数,那么如果存在众数,最后留下的数肯定是众数。
int MoreThanHalfNum_Solution(vector<int> numbers) {
if (numbers.empty()) return 0; // 遍历每个元素,并记录次数;若与前一个元素相同,则次数加1,否则次数减1
int result = numbers[0]; int times = 1; // 次数
for(int i=1;i<numbers.size();++i)
{
if(times != 0)
{
if(numbers[i] == result)
{
++times;
}
else { --times; }
}
else { result = numbers[i]; times = 1; }
}// 判断result是否符合条件,即出现次数大于数组长度的一半
times = 0;
for(int i=0;i<numbers.size();++i)
{
if(numbers[i] == result) ++times;
}
return (times > numbers.size()/2) ? result : 0;
}
定义map,使用<数字,次数>的映射关系,最后统计每个字符出现的次数
int MoreThanHalfNum_Solution(vector<int> numbers) {
unordered_map<int, int> map;
int half = numbers.size() / 2;
for (int i = 0; i < numbers.size(); i++)
{
auto it = map.find(numbers[i]); //如果已经在map中,进行自增,如果不在,插入,首次出现
if( it != map.end() )
{ map[numbers[i]]++; }
else
{map.insert(make_pair(numbers[i], 1)); }
//自增或者插入一个,直接进行判定。注意,这里要考虑测试用例为{1}的情况
//走到这里,对应的key val一定存在
if(map[numbers[i]] > half)
{ return numbers[i]; }
}//走到这里,说明没有找到
return 0; }
们同时去掉两个不同的数字,到最后剩下的一个数就是 该数字。如果剩下两个,那么这两个也是一样的,就是结果),在其基础上把最后剩下的一个数字或者两个回到原来数组中, 将数组遍历一遍统计一下数字出现次数进行最终判断。
从前往后,把偶数后移,腾出位置,放入奇数
nt MoreThanHalfNum_Solution(vector<int> numbers) {
if (numbers.size() == 0)
{ return 0; }
int number = numbers[0]; int times = 1;
for (int i = 1; i < numbers.size(); i++)
{
if (times == 0){ //如果当前times是0,说明之前的不同抵消完了
number = numbers[i];
times = 1; }
else if(numbers[i] == number)
{ times++; }
else
{times--; }
}//如果输入本身满足条件,则times一定>0, 并且number保存的就是准目标,再次确认
int count = 0;
for(int i = 0; i < numbers.size(); i++)
{ if(numbers[i] == number)
{ count++; }
}
return count > numbers.size()/2 ? number : 0; }
704. 二分查找
循环不变量原则:循环中坚持对区间的定义,才能清楚的把握循环中的各种细节。只要看到面试题里给出的数组是有序数组,都可以想
一想是否可以使用二分法
添加链接描述
// 定义target在左闭右开的区间里,即:[left, right)
class Solution {
public:
int search(vector<int>& nums, int target) {
int left = 0;
int right = nums.size();
while (left < right) {
int middle = left + ((right - left) >> 1);
if (nums[middle] > target) {
right = middle; // target 在左区间,在[left, middle)中
} else if (nums[middle] < target) {
left = middle + 1; // target 在右区间,在[middle + 1, right)中
} else { // nums[middle] == target
return middle; // 数组中找到目标值,直接返回下标
}
}
// 未找到目标值
return -1;
}
};
旋转数组的最小数字
添加链接描述

原始数组是非递减的,旋转之后,就有可能出现递减,引起递减的数字,就 是最小值;旋转后的数组可以看做成两部分,前半部分整体非递减,后半部分整体非递减,前半部分整体大于后半部分。
int minNumberInRotateArray(vector<int> rotateArray) {
if (rotateArray.empty()){ return 0; }
int left = 0; int right = rotateArray.size() - 1;
int mid = 0; //要一直满足该条件,以证明旋转特性
while(rotateArray[left] >= rotateArray[right])
{
if(right - left == 1)
{ //两个下标已经相邻了
mid = right; break; }
mid = left + ((right - left) >> 1); //注意操作符优先级
if(rotateArray[mid] == rotateArray[left] && rotateArray[left] == rotateArray[right])
{ //无法判定目标数据在mid左侧,还是右侧我们采用线性遍历方式
int result = rotateArray[left];
for(int i = left+1; i < right; i++)
{ if(result > rotateArray[i])
{ result = rotateArray[i]; }
}
return result;
}
if(rotateArray[mid] >= rotateArray[left]){ //试想两者相等, 隐含条件
//rotateArray[left] >= rotateArray[right] //说明mid在前半部分
left = mid; }
else{
//说明mid在后半部分
right = mid; }
}
return rotateArray[mid];
}
调整数组顺序使奇数位于偶数前面
void reOrderArray(vector<int> &array) {
int k = 0; for (int i = 0; i < array.size(); ++i){
if (array[i] & 1)奇数
{ //从左向右,每次遇到的,都是最前面的奇数,一定将来要被放在k下标处
int temp = array[i]; //现将当前奇数保存起来
int j = i;
while(j > k)
{ //将该奇数之前的内容(偶数序列),整体后移一个位置
array[j] = array[j-1]; j--; }
array[k++] = temp; k:移动到哪里就不移动了
//将奇数保存在它将来改在的位置,因为我们是从左往右放的,没有跨越奇 数,所以一定是相对位置不变的
}k:第1个奇数、第2个奇数……
}
}
vectorres(r, vector(c, 0));初始化r行 c列 初试为0的元素
























 622
622

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








