Python计算机视觉编程第五章多视图几何_多视图几何 pnp-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_55871320/article/details/142223754

外极几何

多视图几何是利用在不同视点所拍摄图像间的关系，来研究照相机之间或者特征之间关系的一门科学。图像的特征通常是兴趣点，多视图几何中最重要的内容是双视图几何。
如果有一个场景的两个视图以及视图中的对应图像点，那么根据照相机间的空间相对位置关系、照相机的性质以及三维场景点的位置，可以得到对这些图像点的一些几何关系约束。我们通过外极几何来描述这些几何关系。
利用照相机方程，可以将上述问题描述为： $\lambda x=PX=PH^{-1}HX=\hat{P}\hat{H}$
因此，当我们分析双视图几何关系时，总是可以将照相机间的相对位置关系用单应性矩阵加以简化。下面是一个好的做法： $P_{1}=K_{1}\left [ I\mid 0 \right ]$ 和 $P_{2}=K_{2}\left [ R \mid t \right ]$
同一个图像点经过不同的投影矩阵产生的不同投影点必须满足： $x_{2}^{T}Fx_{1}=0$ ,其中， $F=K_{2}^{-T}S_{t}RK_{1}^{-1}$

一个简单的数据集

我们这里使用一个牛津多视图数据集；从http://www.robots.ox.ac.uk/~vgg/data/datamview.html 可以下载Merton1 数据的压缩文件。下面的脚本可以加载Merton1的数据：

import camera
 # 载入一些图像
im1 = array(Image.open('images/001.jpg'))
im2 = array(Image.open('images/002.jpg'))
 # 载入每个视图的二维点到列表中
points2D = [loadtxt('2D/00'+str(i+1)+'.corners').T for i in range(3)]
 # 载入三维点
points3D = loadtxt('3D/p3d').T
 # 载入对应
corr = genfromtxt('2D/nview-corners',dtype='int',missing='*')
 # 载入照相机矩阵到Camera对象列表中
P = [camera.Camera(loadtxt('2D/00'+str(i+1)+'.P')) for i in range(3)]

上面的程序会加载前两个图像（共三个）、三个视图中的所有图像特征点1、对应不同视图图像点重建后的三维点以及照相机参数矩阵。
下面来可视化这些数据。将三维的点投影到一个视图，然后和观测到的图像点比较：

# 将三维点转换成齐次坐标表示，并投影
X = vstack( (points3D,ones(points3D.shape[1])) )
 x = P[0].project(X)
 # 在视图1中绘制点
figure()
 imshow(im1)
 plot(points2D[0][0],points2D[0][1],'*')
 axis('off')
 figure()
 imshow(im1)
 plot(x[0],x[1],'r.')
 axis('off')
 show()

运行结果如下：
在这里插入图片描述

用Matplotlib绘制三维数据

Matplotlib中的mplot3d工具包可以方便地绘制出三维点、线、等轮廓线、表面以及其他基本图形组件，还可以通过图像窗口控件实现三维旋转和缩放。
可以通过在axes对象中加上projection="3d"关键字实现三维绘图，如下：

from mpl_toolkits.mplot3d import axes3d
fig = figure()
ax = fig.gca(projection="3d")
 # 生成三维样本点
X,Y,Z = axes3d.get_test_data(0.25)
 # 在三维中绘制点
ax.plot(X.flatten(),Y.flatten(),Z.flatten(),'o')
show()

结果如下：
在这里插入图片描述

现在通过画出Merton样本数据来观察三维点的效果：

# 绘制三维点
from mpl_toolkits.mplot3d import axes3d
fig = figure()
ax = fig.gca(projection='3d')
ax.plot(points3D[0],points3D[1],points3D[2],'k.')

下面是使用Matplottib工具包绘制的，牛津multi-view数据库中Mertoln1数据集的三维点：从上面和侧边观测的视图（左）；俯视的视图，展示了建筑墙体和屋顶上的点（中）；侧图，展示了一面墙的轮廓，以及另一面墙上点的主视图（右）
在这里插入图片描述

计算F：八点法

八点法是通过对应点来计算基础矩阵的算法。外极约束可写成下面形式：
$\left[\begin{array}{ccccc}x_{2}^{1} x_{1}^{1} & x_{2}^{1} y_{1}^{1} & x_{2}^{1} w_{1}^{1} & \cdots & w_{2}^{1} w_{1}^{1} \\x_{2}^{2} x_{1}^{2} & x_{2}^{2} y_{1}^{2} & x_{2}^{2} w_{1}^{2} & \cdots & w_{2}^{2} w_{1}^{2} \\\vdots & \vdots & \vdots & \ddots & \vdots \\x_{2}^{n} x_{1}^{n} & x_{2}^{n} y_{1}^{n} & x_{2}^{n} w_{1}^{n} & \cdots & w_{2}^{n} w_{1}^{n}\end{array}\right]\left[\begin{array}{c}\boldsymbol{F}_{11} \\\boldsymbol{F}_{12} \\\boldsymbol{F}_{13} \\\vdots \\\boldsymbol{F}_{33}\end{array}\right]=\boldsymbol{A} \boldsymbol{f}=0$
基础矩阵中有9个元素，由于尺度是任意的，所以只需要8个方程。因为算法中需要8个对应点来计算基础矩阵F，所以该算法叫做八点法。
下面是写入下面八点法中最小化 $\parallel Af\parallel$ 的函数：

def compute_fundamental(x1,x2):
  """使用归一化的八点算法，从对应点（x1，x2 3×n的数组）中计算基础矩阵
    每行由如下构成：
    [x'*x，x'*y' x', y'*x, y'*y, y', x, y, 1]"""
  n = x1.shape[1]
  if x2.shape[1] != n:
    raise ValueError("Number of points don't match.")
# 创建方程对应的矩阵
  A = zeros((n,9))
  for i in range(n):
    A[i] = [x1[0,i]*x2[0,i], x1[0,i]*x2[1,i], x1[0,i]*x2[2,i],
        x1[1,i]*x2[0,i], x1[1,i]*x2[1,i], x1[1,i]*x2[2,i],
        x1[2,i]*x2[0,i], x1[2,i]*x2[1,i], x1[2,i]*x2[2,i] ]
# 计算线性最小二乘解
  U,S,V = linalg.svd(A)
  F = V[-1].reshape(3,3)
  # 受限F
  # 通过将最后一个奇异值置0，使秩为2
  U,S,V = linalg.svd(F)
  S[2] = 0
  F = dot(U,dot(diag(S),V))
  return F

通常用SVD算法来计算最小二乘解。上面的函数忽略了一个重要的步骤：对图像坐标
进行归一化，这可能会带来数值问题。

外极点和外极线

外极点满足 $Fe_{1}=0$ ,可以通过计算F的零空间来得到。使用下面函数可以得到：

def compute_epipole(F):
  """ 从基础矩阵F中计算右极点（可以使用F.T获得左极点）"""
  # 返回F的零空间（Fx=0）
  U,S,V = linalg.svd(F)
  e = V[-1]
 return e/e[2]

我们可以在之前样本数据集的前两个视图上运行这两个函数：

import sfm
 # 在前两个视图中点的索引
ndx = (corr[:,0]>=0) & (corr[:,1]>=0)
 # 获得坐标，并将其用齐次坐标表示
x1 = points2D[0][:,corr[ndx,0]]
 x1 = vstack( (x1,ones(x1.shape[1])) )
 x2 = points2D[1][:,corr[ndx,1]]
 x2 = vstack( (x2,ones(x2.shape[1])) )
 # 计算F
 F = sfm.compute_fundamental(x1,x2)
 # 计算极点
e = sfm.compute_epipole(F)
 # 绘制图像
figure()
 imshow(im1)
 # 分别绘制每条线，这样会绘制出很漂亮的颜色
for i in range(5):
  sfm.plot_epipolar_line(im1,F,x2[:,i],e,False)
 axis('off')
 figure()
 imshow(im2)
 # 分别绘制每个点，这样会绘制出和线同样的颜色
for i in range(5):
  plot(x2[0,i],x2[1,i],'o')
axis('off')
show()

上面的函数将x轴的范围作为直线的参数，因此直线超出图像边界的部分会被截断。
程序运行如下：
在这里插入图片描述

照相机和三维结构的计算

三角剖分

给定照相机参数模型，图像点可以通过三角剖分来恢复出这些点的三维位置。基本的算法思想如下。
对于两个照相机P1和P2的视图，三维实物点X的投影点为x1和x2，照相机方程定义了下列关系： $\left[\begin{array}{ccc}P_{1} & -\mathbf{x}_{1} & 0 \\P_{2} & 0 & -\mathbf{x}_{2}\end{array}\right]\left[\begin{array}{l}\mathbf{X} \\\lambda_{1} \\\lambda_{2}\end{array}\right]=0$
下面使用一个函数来计算一个点对的最小二乘三角剖分

def triangulate_point(x1,x2,P1,P2):
  """ 使用最小二乘解，绘制点对的三角剖分"""
  M = zeros((6,6))
  M[:3,:4] = P1
  M[3:,:4] = P2
  M[:3,4] = -x1
  M[3:,5] = -x2
  U,S,V = linalg.svd(M)
  X = V[-1,:4]
  return X / X[3]

可以增加下面的函数来实现多个点的三角剖分：

def triangulate(x1,x2,P1,P2):
  """ x1 和 x2（3×n 的齐次坐标表示）中点的二视图三角剖分"""
  n = x1.shape[1]
  if x2.shape[1] != n:
      raise ValueError("Number of points don't match.")
  X = [ triangulate_point(x1[:,i],x2[:,i],P1,P2) for i in range(n)]
  return array(X).T

可以利用下面的代码来实现Merton1数据集上的三角剖分：

ndx = (corr[:,0]>=0) & (corr[:,1]>=0)
 # 获取坐标，并用齐次坐标表示
x1 = points2D[0][:,corr[ndx,0]]
x1 = vstack( (x1,ones(x1.shape[1])) )
x2 = points2D[1][:,corr[ndx,1]]
x2 = vstack( (x2,ones(x2.shape[1])) )
Xtrue = points3D[:,ndx]
Xtrue = vstack( (Xtrue,ones(Xtrue.shape[1])) )
# 检查前三个点
Xest = sfm.triangulate(x1,x2,P[0].P,P[1].P)
print Xest[:,:3]
print Xtrue[:,:3]
 # 绘制图像
from mpl_toolkits.mplot3d import axes3d
fig = figure()
ax = fig.gca(projection='3d')
ax.plot(Xest[0],Xest[1],Xest[2],'ko')
ax.plot(Xtrue[0],Xtrue[1],Xtrue[2],'r.')
axis('equal')
show()

运行结果如下：
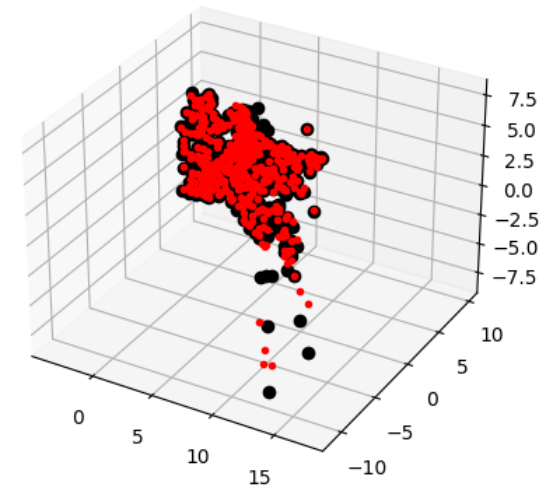
在这里插入图片描述

由三维点计算照相机矩阵

我们可以使用直接线性变换的方法来计算照相机矩阵P。本质上，这是三角剖分方法的逆问题，有时我们将其称为照相机反切法。
每个三维点 $X_{i}$ 按照 $\lambda _{i} x_{i}=PX_{i}$ 投影到图像点 $x_{i}=\left [ x_{i},y_{i},1 \right ]$ ,相应的点满足下面的关系：在这里插入图片描述
然后，我们可以使用SVD分解估计出照相机矩阵。代码如下

def compute_P(x,X): 
  """ 由二维- 三维对应对（齐次坐标表示）计算照相机矩阵"""
  n = x.shape[1]
  if X.shape[1] != n:
    raise ValueError("Number of points don't match.")
  # 创建用于计算DLT解的矩阵
  M = zeros((3*n,12+n))
  for i in range(n):
    M[3*i,0:4] = X[:,i]
    M[3*i+1,4:8] = X[:,i]
    M[3*i+2,8:12] = X[:,i]
    M[3*i:3*i+3,i+12] = -x[:,i]
  U,S,V = linalg.svd(M)
  return V[-1,:12].reshape((3,4))

下面的代码会选出第一个视图中的一些可见点，将它们转换为齐次坐标表示，然后估计照相机矩阵：

import sfm, camera
 corr = corr[:,0] # 视图 1
 ndx3D = where(corr>=0)[0] # 丢失的数值为-1
 ndx2D = corr[ndx3D]
 # 选取可见点，并用齐次坐标表示
x = points2D[0][:,ndx2D] # 视图 1
 x = vstack( (x,ones(x.shape[1])) )
 X = points3D[:,ndx3D]
 X = vstack( (X,ones(X.shape[1])) )
 # 估计P
 Pest = camera.Camera(sfm.compute_P(x,X))
 # 比较！
print Pest.P / Pest.P[2,3]
print P[0].P / P[0].P[2,3]
 
xest = Pest.project(X)
 # 绘制图像
figure()
 imshow(im1)
 plot(x[0],x[1],'bo')
 plot(xest[0],xest[1],'r.')
 axis('off')
 show()

输出如下：
在这里插入图片描述

真实点用圆圈表示，估计出的照相机投影点用点表示。

多视图重建

假设照相机已经标定，计算重建可以分为下面4个步骤：
(1) 检测特征点，然后在两幅图像间匹配；
(2) 由匹配计算基础矩阵；
(3) 由基础矩阵计算照相机矩阵；
(4) 三角剖分这些三维点。

稳健估计基础矩阵

代码如下：

class RansacModel(object):
  """ 用从 http://www.scipy.org/Cookbook/RANSAC 下载的 ransac.py 计算基础矩阵的类 """
  def __init__(self,debug=False):
    self.debug = debug
  def fit(self,data):
    """ 使用选择的 8 个对应计算基础矩阵"""
    # 转置，并将数据分成两个点集
    data = data.T
    x1 = data[:3,:8]
    x2 = data[3:,:8]
    #估计基础矩阵，并返回 
    F = compute_fundamental_normalized(x1,x2)
    return F
  def get_error(self,data,F):
    """ 计算所有对应的 x^T F x，并返回每个变换后点的误差"""
    # 转置，并将数据分成两个点集
    data = data.T
    x1 = data[:3]
    x2 = data[3:]
    # 将Sampson 距离用作误差度量
    Fx1 = dot(F,x1)
    Fx2 = dot(F,x2)
    denom = Fx1[0]**2 + Fx1[1]**2 + Fx2[0]**2 + Fx2[1]**2
    err = ( diag(dot(x1.T,dot(F,x2))) )**2 / denom
    # 返回每个点的误差
    return err