性能优化
(1)动量法:

(2)自适应梯度

(3)RMSProp算法

(4)Adam算法

(5)K折交叉验证
原始训练数据被分成K个不重叠的子集。 然后执行 K 次模型 训练和验证,每次在 K−1 个子集上进行训练, 并在剩余的一 个子集(在该轮中没有用于训练的子集)上进行验证。 最后, 通过对 K 次实验的结果取平均来估计训练和验证误差。 (6)欠拟合和过拟合
欠拟合:误差一直比较大
过拟合:在训练数据集上误差小而在测试数据集上误差大
(7)权重衰减(L2正则化)
为防止过拟合和权值震荡,加入新的指标函数项:

第二项约束了权值不能过大。在梯度下降时,导数容易计算:

(8)模型初始化
简单初始化:把所有权值在[-1,1]区间内按均值或高斯分布 进行初始化。
Xavier初始化:为了使得网络中信息更好的流动,每一层输 出的方差应该尽量相等。因此需要实现下面的均匀分布:

卷积神经网络基础
(1)PyTorch的基本使用
构建简单的计算图,每个节点将零个或多个tensor作为输入,产生一个 tensor作为输出。PyTorch中,所见即为所得,tensor的使用和numpy中的多 维数组类似:


(2)线性回归
定义网络

进行训练

得到结果

(3)基本概念
全连接网络:链接权过多,难算难收敛,同时可 能进入局部极小值,也容易产生过拟合问题
局部连接网络:顾名思义,只有一部分权值连接。 部分输入和权值卷积。
填充(Padding):也就是在矩阵的边界上填充一些值,以 增加矩阵的大小,通常用0或者复制边界像素来进行填充。

步长(Stride):如图步长为2

多通道卷积:如RGB


池化(Pooling)
思想:使用局部统计特征,如均值或最大值。解 决特征过多问题

卷积神经网络结构
构成:由多个卷积层和下采样层构成,后面可连 接全连接网络
卷积层:k个滤波器 下采样层:采用mean或max 后面:连着全连接网络

学习算法
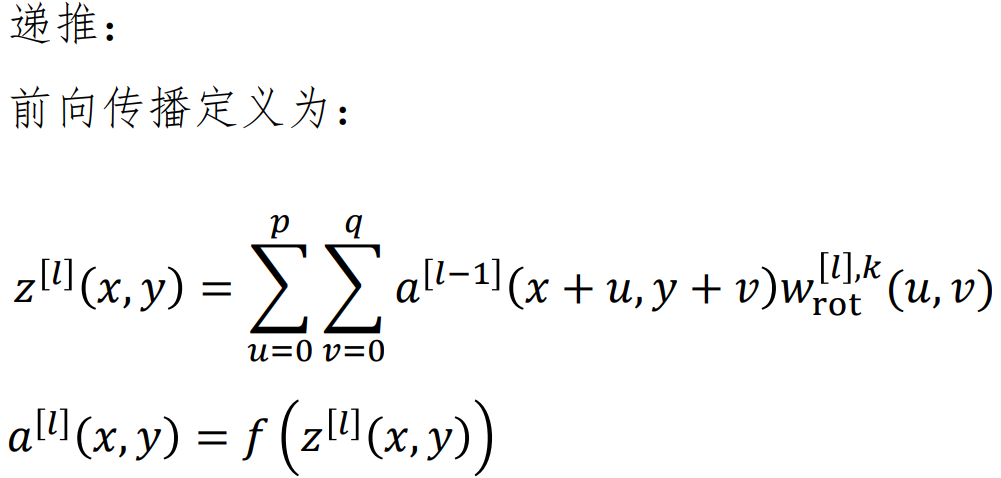

(4)LeNet-5网络
网络结构

C1层
6个Feature map构成 ,每个神经元对输入进行5*5卷积 每个神经元对应5*5+1个参数,共6个feature map, 28*28个神经元,因此共有 (5*5+1)*6*(28*28)=122,304连接。
S2层
Pooling层

C3层
卷积层

S4层
与S2层工作原理相同

C5层
120个神经元 ,每个神经元同样对输入进行5*5卷积,与S4全连接 ,总连接数(5*5*16+1)*120=48120。
F6层
84个神经元 ,与C5全连接 ,总连接数(120+1)*84=10164。
输出层
由欧式径向基函数单元构成 ,每类一个单元 ,输出RBF单元计算输入向量和参数向量之间的欧式距离。
网络结构说明

随网络深入,宽、高衰减,通道数增加
卷积NN的BP算法:下采样层
如果当前是卷积层,下一层为下采样层,误差如何从下采样层回传 ,假设为2*2核平均池化


如果当前是下采样层,下一层为卷积层,误差如何从卷积回传 ,假设为2*2核卷积。

卷积核为:


式中五角星表示图像卷积,计算时需首先上下、左右翻转后再做相关(点乘)。
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








