二分查找法

一、二分查找的原理

二分查找的实现原理非常简单，首先要有一个有序的列表。但是如果没有，则该怎么办？可以使用排序算法进行排序。

以升序数列为例，比较一个元素与数列中的中间位置的元素的大小，如果比中间位置的元素大，则继续在后半部分的数列中进行二分查找；如果比中间位置的元素小，则在数列的前半部分进行比较；如果相等，则找到了元素的位置。每次比较的数列长度都会是之前数列的一半，直到找到相等元素的位置或者最终没有找到要找的元素。

我们先来想象一下，如果数列中有 3 个数，则先与第 2 个数进行比较，如果比第 2 个数大，则与第 2 个数右边的数列进行二分查找，这时这个数列就剩下一个数了，直接比较是否相等即可。所以在 3 个数的时候最多比较两次。

同理，在有 4 个数的时候，我们与中间数进行比较，一般中间数是首加末除以 2 算出来的，这时我们算出来的中间数是 (1+4)/2 等于 2，所以我们把要查找的数与第 2 个数比较，若比第 2 个数小，则直接与第 1 个数比较；否则与后面两个数进行二分查找，这时的中间数是 (3+4)/2 等于 3，也就是后半部分的第 1 个数。再接着进行比较，相等则找到相应的元素，小于则没有这个数（因为左边所有的数都已经判断过了），大于则继续向右查找。所以在 4 个数的时候最多比较 3 次。

以此类推，在 5 个数的时候最多查找 3 次，在 6 个数的时候也是最多查找 3 次。

下面我们以一个实际的例子来看看二分查找的操作过程。假设待查找数列为 1、3、5、7、9、11、19，我们要找的元素为 18，下面进行二分查找。首先待查数列如图 1 所示，我们找到中间的元素 7（ (1+7)/2=4，第 4 个位置上的元素）。
 

图 1 在待查序列中找到中间元素

中间元素为 7，我们要找的元素比 7 大，于是在后半部分查找，现在后半部分数列为 9、11、19，我们找到中间元素，如图 2 所示。
 

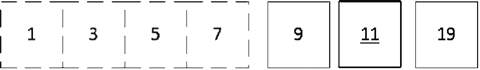
图 2 在待查序列的后半部分找到中间元素

中间元素为 11，与 11 比较，比 11 大，则继续在后半部分查找，后半部分只有一个元素 19 了，这时直接与 19 比较，若不相等，则说明在数列中没有找到元素，结束查找。

二、程序实现

1、递归法实现（二分查找）

程序：

bool my_lookup(const int* arr,const int t,int left,int right)    //如果找到返回真，否则返回假
{
	int mid = (left + right) / 2;
	if (left > right)    //当左标记大于右标记说明未找到，返回假
		return 0;
	if (t == arr[mid])   //找到了，返回值
		return 1;
//查询过程中，进行递归
	else if(t > arr[mid])
	{
		if (my_lookup(arr, t, mid + 1, right))
			return 1;
		else
			return 0;
	}
	else
	{
		if (my_lookup(arr, t,left,mid-1))
			return 1;
		else
			return 0;
	}
}

运行结果：

        当数组为：1,2,3,4,5,6,7,8,9,13,18,20  

2、循环实现（二分查找）

程序：

void my_lookup(const int* arr, const int t,const int len)
{
	int left = 0;
	int right = len - 1;
	int mid;
	int flag = 1;
	while (right >=left)
	{
		mid = (left + right) / 2;
		if (arr[mid] == t)
		{
			cout << "找到了" << endl;
			return;            //找到了，跳出函数体
		}
    //继续查询
		else if (arr[mid] < t)
		{
			left = mid + 1;
		}
		else
		{
			right = mid - 1;
		}
	}
	if (flag)    
	{
		cout << "未找到" << endl;
	}
}

运行结果：

   当数组为：1,2,3,4,5,6,7,8,9,13,18,20