蓝桥杯试题 算法训练 绘制地图—O(n)复杂度重建整棵树

问题描述

　　最近，WYF正准备参观他的点卡工厂。WYF集团的经理氰垃圾需要帮助WYF设计参“观”路线。现在，氰垃圾知道一下几件事情：
　　1.WYF的点卡工厂构成一颗二叉树。
　　2.一共有n座工厂。
　　3.他需要把这颗树上的点以后序遍历的方法列出来，才能绘制地图。
　　还好，最近他的属下给了他先序遍历和中序遍历的数据。可是，氰垃圾最近还要帮㊎澤穻解决一些问题，没有时间。请你帮帮他，替他完成这项任务。由于氰垃圾的一些特殊的要求，WYF的参观路线将会是这棵树的后序遍历。

输入格式

　　第一行一个整数n，表示一共又n座工厂。
　　第二行n个整数，表示先序遍历。
　　第三行n个整数，表示中序遍历。

输出格式

　　输出共一行，包含n个整数，为后序遍历。

 

试题分析：由于给了节点编号 所以直接用下标索引储存树

算法过程：
pre[n]为前序序列 in[n]为中序序列 vis[n]记录是否已在前序序列中出现

初始两个下标  cur1＝0,cur2＝0
1.当pre[cur1]!＝in[cur2]时 cur1往前进一格，并且pre[cur1]号结点的左孩子为pre[cur1+1]号结点 并记录vis[pre[cur1+1]]＝1

while (in[cur2] != pre[cur1]) {
			tree[pre[cur1]].left = pre[cur1 + 1];
			vis[pre[cur1 + 1]] = 1;
			cur1++;
		}

2.此时pre[cur1]＝＝in[cur2]，我们让cur2前进，直到in[cur2]号结点未出现过，即vis[in[cur2]]＝0

		while (vis[in[cur2]]) {
			cur2++;
		}

3.这时令in[cur2-1]号结点右孩子为pre[cur1+1]，cur1前进一格

		tree[in[cur2 - 1]].right = pre[cur1 + 1];
		vis[pre[cur1+1]] = 1;
		cur1++;

重复1,2,3 直至cur1或cur2走到终点

下面演示一组例子 绿色代表中序序列的进展 黄色代表通过步骤3连结的节点

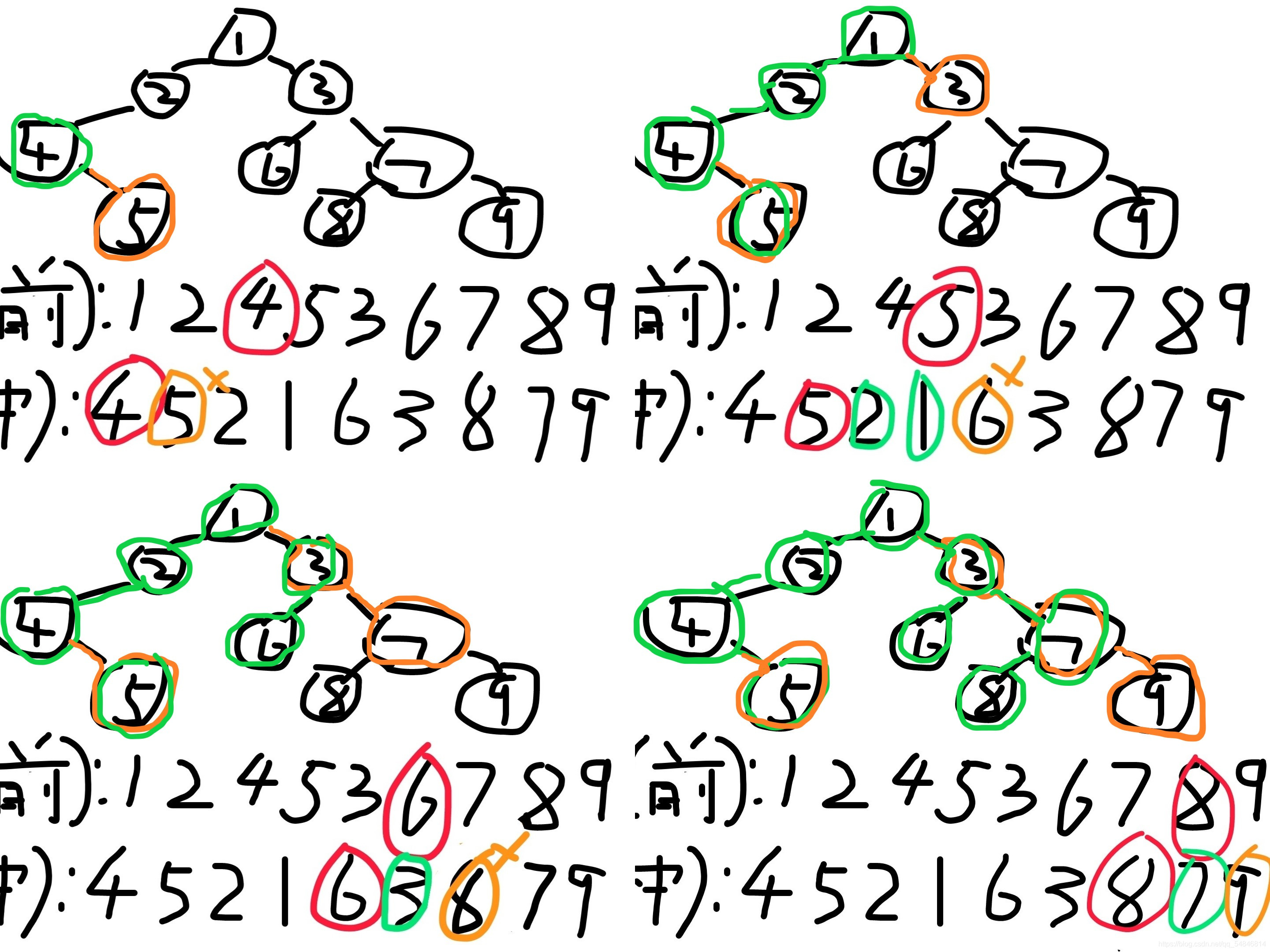
下面证明每次中序序列前进时第一个未在前序序列中出现的节点的前一个结点是前序序列中下一个结点的父亲(父亲和右孩子)
由于该点的前一个点在已经遍历过的前序序列中出现，那么因为中序遍历的性质，前一个点的左子树上任一个点必在该点之前被遍历到，即前一点左子树上任意一点已在先序序列中出现过，并且由中序遍历性质还可得到该点为前一个点的右子树上的结点(反证法：显然该点不可能在前一点的左子树，如果为前一点的父亲/长辈结点，那么该点一定在前序序列中出现过 从而产生矛盾)而且为右子树上最左的节点。那么因为在前序遍历中右子树上最左的结点都没有出现过，从而整棵右子树上的结点都没有出现过，综上：
1.前一个结点的左子树在前序遍历中已经遍历完
2.前一个结点的右子树在前序遍历中没有被遍历过
那么可以得出结论前一个点的右孩子就是前序遍历序列中的下一个结点。

复杂度分析：显然这里cur1和cur2不会回退 时间复杂度O(n);

#include<bits/stdc++.h>
using namespace std;
int	n;
struct bitnode {
	int left, right;
	bitnode() :left(0), right(0) {}
};
const int maxn = 1e5 + 5;
int pre[maxn], in[maxn], vis[maxn];
int root;
bitnode tree[maxn];
void solve() {
	root = pre[0];
	vis[pre[0]] = 1;
	int cur1 = 0, cur2 = 0;
	while (cur1 < n - 1 || cur2 < n - 1) {
	//当pre[cur1]!＝in[cur2]时 cur1往前进一格
	//并且pre[cur1]号结点的左孩子为pre[cur1+1]号结点 并记录vis[pre[cur1+1]]＝1
		while (in[cur2] != pre[cur1]) {
			tree[pre[cur1]].left = pre[cur1 + 1];
			vis[pre[cur1 + 1]] = 1;
			cur1++;
		}
	//此时pre[cur1]＝＝in[cur2]，我们让cur2前进，直到in[cur2]号结点未出现过，即vis[in[cur2]]＝0
		while (vis[in[cur2]]) {
			cur2++;
		}
	//这时令in[cur2 - 1]号结点右孩子为pre[cur1 + 1]，cur1前进一格
		tree[in[cur2 - 1]].right = pre[cur1 + 1];
		vis[pre[cur1+1]] = 1;
		cur1++;
	}
}
void posterorder(int root)
{
	if (tree[root].left) {
		posterorder(tree[root].left);
	}
	if (tree[root].right) {
		posterorder(tree[root].right);
	}
	cout << root << " ";
}
int main() {
	cin >> n;
	for (int i = 0; i < n; i++) {
		cin >> post[i];
	}
	for (int i = 0; i < n; i++) {
		cin >> in[i];
	}
	clock_t s = clock();
	solve();
	clock_t e = clock();
	//cout << e - s;
	posterorder(root);
	return 0;
}