机器学习-----朴素贝叶斯

目录
一 基本概念
1 简介
2 朴素贝叶斯的优缺点
2 先验概率和后验概率
3 条件概率与全概率公式
4 贝叶斯推断
二 贝叶斯分类器的简单应用
1 数据说明
2 进行分类
三 朴素贝叶斯过滤垃圾邮件
1 流程说明
2 构建词向量
3 词向量计算概率
4 朴素贝叶斯分类函数
5 使用朴素贝叶斯进行交叉验证
四 总结
 

一、基本概念

1.简介

最为广泛的两种分类模型是决策树模型(Decision Tree Model)和朴素贝叶斯模型（Naive Bayesian Model，NBM）。和决策树模型相比，朴素贝叶斯分类器(Naive Bayes Classifier 或 NBC)发源于古典数学理论，有着坚实的数学基础，以及稳定的分类效率。同时，NBC模型所需估计的参数很少，对缺失数据不太敏感，算法也比较简单。理论上，NBC模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为NBC模型假设属性之间相互独立，这个假设在实际应用中往往是不成立的，这给NBC模型的正确分类带来了一定影响。

2.贝叶斯的优缺点

朴素贝叶斯的主要优点有：

1）朴素贝叶斯模型发源于古典数学理论，有稳定的分类效率。

2）对小规模的数据表现很好，能个处理多分类任务，适合增量式训练，尤其是数据量超出内存时，我们可以一批批的去增量训练。

3）对缺失数据不太敏感，算法也比较简单，常用于文本分类。

朴素贝叶斯的主要缺点有：

1） 理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是如此，这是因为朴素贝叶斯模型假设属性之间相互独立，这个假设在实际应用中往往是不成立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。而在属性相关性较小时，朴素贝叶斯性能最为良好。对于这一点，有半朴素贝叶斯之类的算法通过考虑部分关联性适度改进。

2）需要知道先验概率，且先验概率很多时候取决于假设，假设的模型可以有很多种，因此在某些时候会由于假设的先验模型的原因导致预测效果不佳。

3）由于我们是通过先验和数据来决定后验的概率从而决定分类，所以分类决策存在一定的错误率。

4）对输入数据的表达形式很敏感。

3.先验概率和后验概率

P(cj)代表还没有训练模型之前，根据历史数据/经验估算cj 拥有的初始概率。P(cj)常被称为cj的先验概率(prior probability) ， 它反映了cj的概率分布，该分布独立于样本。

通常可以用样例中属于cj的样例数|cj|比上总样例数|D|来

近似，即：

4.条件概率与全概率公式

 

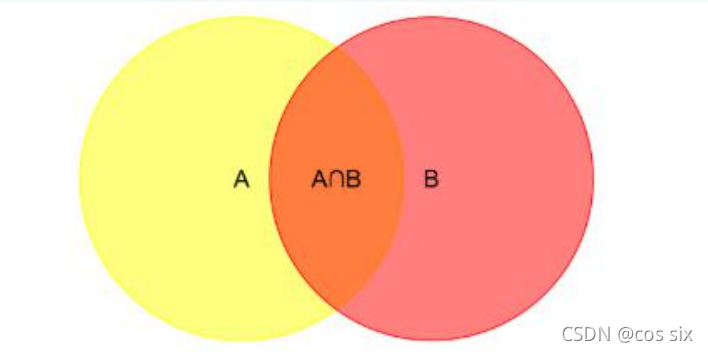
已知两个独立事件A和B，事件B发生的前提下，事件A发生的概率可

以表示为P(A|B)，即上图中橙色部分占红色部分的比例，即：

 5. 贝叶斯推断

根据条件概率和全概率公式，可以得到贝叶斯公式如下：

 

P(A) 称