定义栈的数据结构并得到最小元素

题目描述：定义栈的数据结构，请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中，调用 min、push 及 pop 的时间复杂度都是 O(1)

栈的数据结构都是很简单的，此题的主要难点就是如何在时间复杂度为O(1)的情况下找到最小元素

思路：要想只调用一次函数就得到最小元素，那么最小元素必须是栈顶元素。要达到这个目的，只能是在元素入栈时就比较之后再存放，将最小的较小的元素放在栈顶(注意：这里说的是较小，而不是最小)。对于一个栈来说，随着入栈元素的增加，不一定能将最小的元素放在栈顶，如图：

 

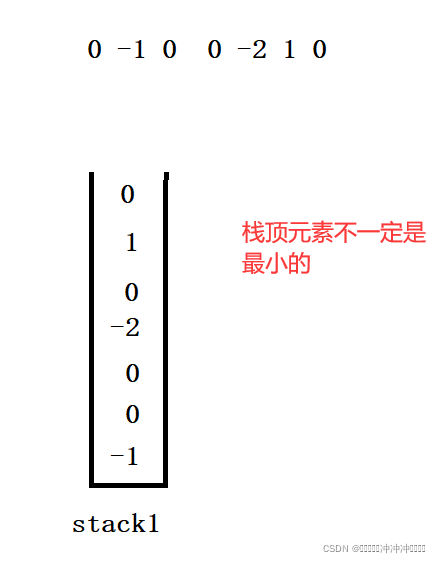
所以我们需要定义两个栈，栈1正常入栈出栈，栈2只存放最小的元素，其它元素不存放，为了达到这个目的，我们只需将每一次要入栈的元素与栈2的栈顶元素进行比较，将较小的入栈即可(因为每次都要入栈较小的，所以可能栈2中的元素都是相同的，但是能保证是最小的)

代码实现：

class MinStack {
    stack<int>st;
    stack<int>minStack;
public:
    MinStack() {
        while(!st.empty())
        {
            st.pop();
        }
        while(!minStack.empty())
        {
            minStack.pop();
        }
        minStack.push(INT_MAX);
    }
    
    void push(int x) {
        st.push(x);
        int minVal=std::min(minStack.top(),x);
        minStack.push(minVal);
    }
    
    void pop() {
     st.pop();
     minStack.pop();
    }
    
    int top() {
        return st.top();
    }
    
    int min() {
        return minStack.top();
    }
};