SVPWM算法原理及详解及永磁同步电机坐标变换（二）

目录

一、SVPWM 8种开关状态

二、六个扇区和扇区判断        

 三、扇区发波

 四、矢量作用时间计算

五、 矢量切换时间的计算

---

一、SVPWM 8种开关状态

        最常见的两电平拓扑如下图:

        共有3个桥臂，每个桥臂只能一个晶闸管通，另一个断开，我们将桥臂上面晶闸管导通，下面关断记为S = 1；下面晶闸管导通，上面关断记为S=0。因此共有种开关状态：

000---001---010---011---100---101---110---111

        其中第一个数字代表a桥臂开关状态，依此类推。

        例如：若a桥臂S=1，b和c桥臂S=0，则我们可以将拓扑结构简化成下面的图：

        其中。

        于是，我们将这八种情况的各相电压总结在下列的表中：

Sa	Sb	Sc
0	0	0	0	0	0	V0
0	0	1				V1
0	1	0				V2
0	1	1				V3
1	0	0				V4
1	0	1				V5
1	1	0				V6
1	1	1	0	0	0	V7

         我们将三相电压写成幅值加相角的形式，令a的相电压相角为0，则b相为120°，c相为240°。并求解他们的矢量和：

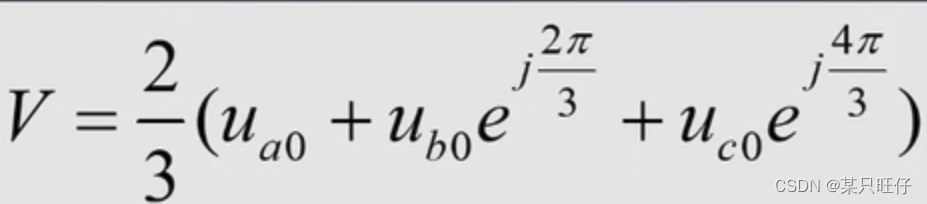
二、六个扇区和扇区判断        

        于是，我们画出上面8种开关状态三相构成矢量和V0,V1,V2,V3,V5,V6,V7，并划分出了六个扇区。

          

         接下来，考虑到我们有一个圆形旋转参考电压，我们需要利用扇区两侧的矢量来合成跟踪参考电压的实际电压。于是，我们就需要判断当前时刻落在哪一个扇区内。

        在SVPWM算法原理及详解及永磁同步电机坐标变换（一）中，我们已经详细的讲述了Clarke变换，也就是 由三相静止坐标系abc到两相静止坐标系αβ的变换，我们将已经合成的参考电压沿着α轴和β轴进行分解。

        并观察每个扇区内值的特征，总结如下表：

         根据以上总结，我们发现可以用一下三个式子来判断扇区：

         

 三、扇区发波

七段式SVPWM矢量如何从起点到达终点？

以第一扇区为例：可以选择红色曲线的顺序发波，也可以选择蓝色曲线。

红色曲线：先沿V4方向走再沿V6方向走，最后再往V4方向走

蓝色曲线：先沿V6方向走再沿V4方向走，最后再往V6方向走

唯一的区别是零矢量的插入方式不同：

        红色路径是4-6-4，因为还是为了每次只切换一个桥臂的开关，零矢量的插入方式是0-4-6-7-6-4-0（7段式），或者是4-6-7-6-4（五段式）；而蓝色路径零矢量的插入方式是7-6-4-0-4-6-7（7段式），或者是6-4-0-4-6（五段式）。

把其他扇区都加进来，就得到下图：

        如果考虑软件的计算方便，每次发波都先发000矢量，中间插入111矢量，那么就要按照图中红色曲线发波，如下图。

        这样第一扇区要先发U4，矢量走到第二扇区后，不能先发U6，要先发距离000更近的矢量U2，到第三扇区后，还是先发U2。总之，1（001），2（010），4（100）距离零矢量（000）更近，要作为每个扇区的首发。

        也可以选择3（011），5（101），6（110）作为首发，那么在7段式的中间需要插入的就是000矢量。

 其他发波形式可以看：SVPWM分析、各个扇区详细计算以及Matlab仿真_michaelf的博客-优快云博客_svpwm扇区判断

 四、矢量作用时间计算

        以下仅介绍第一扇区的计算方式，其他扇区计算方式相同：

 

 

五、 矢量切换时间的计算

 

 未完待续