第十一届蓝桥软件类JavaB组

试题 A: 门牌制作
【问题描述】
小蓝要为一条街的住户制作门牌号。
这条街一共有 2020 位住户，门牌号从 1 到 2020 编号。
小蓝制作门牌的方法是先制作 0 到 9 这几个数字字符，最后根据需要将字
符粘贴到门牌上，例如门牌 1017 需要依次粘贴字符 1、0、1、7，即需要 1 个
字符 0，2 个字符 1，1 个字符 7。
请问要制作所有的 1 到 2020 号门牌，总共需要多少个字符 2？
【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一
个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

public class text1 {
    public static void main(String[] args) {
        int sum=0;
        for(int i=1;i<=2020;i++){
            int a=i;
            while(a!=0){
                if(a%10==2) sum++;
                a/=10;
            }
        }
        System.out.println(sum);
    }
}

答案：624

试题 B: 寻找 2020
【问题描述】
小蓝有一个数字矩阵，里面只包含数字 0 和 2。小蓝很喜欢 2020，他想找
到这个数字矩阵中有多少个 2020 。
小蓝只关注三种构成 2020 的方式：
• 同一行里面连续四个字符从左到右构成 2020。
• 同一列里面连续四个字符从上到下构成 2020。
• 在一条从左上到右下的斜线上连续四个字符，从左上到右下构成 2020。
例如，对于下面的矩阵：
220000
000000
002202
000000
000022
002020
一共有 5 个 2020。其中 1 个是在同一行里的，1 个是在同一列里的，3 个
是斜线上的。
小蓝的矩阵比上面的矩阵要大，由于太大了，他只好将这个矩阵放在了一
个文件里面，在试题目录下有一个文件 2020.txt，里面给出了小蓝的矩阵。
请帮助小蓝确定在他的矩阵中有多少个 2020。
【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一
个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

思路：
将矩阵当作字符串存入，每一行与数组下标对应，将txt文件以文本形式存入ecalipse知道有300行，然后对数组遍历即可。

import java.util.Scanner;
public class text2 {
    public static long count=0;
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        String[] str = new String[300];
        for (int i = 0; i < 300; i++) {
            str[i] = sc.nextLine();
        }
        sc.close();
        f(str);
        System.out.println(count);
        sc.close();
    }
    public static void f(String[] str){
        for(int i=0;i<str.length;i++){//length属性是针对数组说的
            for(int j=0;j<str[i].length();j++){//length()方法是针对字符串String说的
                if(str[i].charAt(j)=='2'){
                    //行相等
                    if(str[i].length()-j>=4&&str[i].charAt(j+1)=='0'&&str[i].charAt(j+2)=='2'&&str[i].charAt(j+3)=='0')
                        count++;
                    //列相等
                    if(str.length-i>=4&&str[i+1].charAt(j)=='0'&&str[i+2].charAt(j)=='2'&&str[i+3].charAt(j)=='0')
                        count++;
                    //对角相等
                    if(str[i].length()-j>=4&&str.length-i>=4&&str[i+1].charAt(j+1)=='0'&&str[i+2].charAt(j+2)=='2'&&str[i+3].charAt(j+3)=='0')
                        count++;
                }
            }
        }
    }
}

答案：16520

试题 C: 蛇形填数
【问题描述】
如下图所示，小明用从 1 开始的正整数“蛇形”填充无限大的矩阵。
1 2 6 7 15 …
3 5 8 14 …
4 9 13 …
10 12 …
11 …
…
(1)
容易看出矩阵第二行第二列中的数是 5。请你计算矩阵中第 20 行第 20 列
的数是多少？
【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一
个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

思路1：
观察第一行斜角的方向的数个数与第一行的列对应数字个数相同，第n行n列对应有2*n-1个斜行加上n个数即可

public class text3 {
        public static void main(String[] args) {
            int sum=0;
            for(int i=1;i<=38;i++){
                sum+=i;
            }
            sum=sum+20;
            System.out.println(sum);
        }
}

答案：671

思路2
找规律，列出前四个1，5，13，25
发现这几个数都是两个平方数相加组成
可以得到

arr[n][n]=(n-1)2+n2

思路三
根据斜行奇偶判断

public class text3 {
    static int[][] arr=new int[50][50];

        public static void main(String[] args) {
            f();
            System.out.println(arr[20][20]);
        }
        //蛇形存入数组
        public static void f(){
            int n=0;
            for(int i=1;i<50;i++){
                if(i%2==1){//第一行第i个为奇数时,(列)j++，(行)为i-j+1（行相应要递减）
                    for(int j=1;j<=i;j++){
                        arr[i-j+1][j]=++n;
                    }
                }
                else{//第一行为偶数时，（行）j++,(列)为i-j+1(列数要递减）
                    for(int j=1;j<=i;j++){
                        arr[j][i-j+1]=++n;
                    }
                }
            }
        }
}

试题 D: 七段码
【问题描述】
小蓝要用七段码数码管来表示一种特殊的文字。

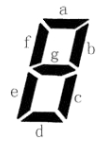
上图给出了七段码数码管的一个图示，数码管中一共有 7 段可以发光的二
极管，分别标记为 a, b, c, d, e, f, g。

小蓝要选择一部分二极管（至少要有一个）发光来表达字符。在设计字符
的表达时，要求所有发光的二极管是连成一片的。
例如：b 发光，其他二极管不发光可以用来表达一种字符。
例如：c 发光，其他二极管不发光可以用来表达一种字符。这种方案与上
一行的方案可以用来表示不同的字符，尽管看上去比较相似。
例如：a, b, c, d, e 发光，f, g 不发光可以用来表达一种字符。
例如：b, f 发光，其他二极管不发光则不能用来表达一种字符，因为发光
的二极管没有连成一片。
请问，小蓝可以用七段码数码管表达多少种不同的字符？
【答案提交】
这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一
个整数，在提交答案时只填写这个整数，填写多余的内容将无法得分。

import java.util.ArrayList;
public class Main {
    static int cnt = 0;
    static boolean[] isVisited = new boolean[7];;//判断是否访问
    static ArrayList<Integer> list[];//临界表
    static boolean[] isCheck = new boolean[1<<8];//不同路径的和不一样
    static int[]arr = new int[7];//暂时记录路径
    public static void main(String[] args) {
        //一个发光：7个
        //两个发光：a-bf; b-gc; c-gd; d-e; e-fg; f-g; 10个
        //三个发光：
        //思路: 构成图（临界表)，然后dfs，检重
        //a:=0; b:=1; c:=2; d:=3; e:=4; f:=5; g:=6;
        list = new ArrayList[7];
        for (int i = 0; i < 7; i++)
            list[i] = new ArrayList<>();

        //a-b
        add(0,1);
        //a-f
        add(0,5);
        //b-c
        add(1,2);
        //b-g
        add(1,6);
        //c-d
        add(2,3);
        //c-g
        add(2,6);
        //d-e
        add(3,4);
        //e-f
        add(4,5);
        //e-g
        add(4,6);
        //f-g
        add(5,6);

        for (int i = 0; i < 7; i++) {
            isVisited[i] = true;
            dfs(i,0);
            isVisited[i] = false;
        }

        System.out.println(cnt);
    }

    private static void dfs(int index,int cur){
        arr[cur] = index;
        if (check(cur))
            return;

        for (int i = 0; i <= cur; i++) {//外循环遍历前面路径的分叉
            for (Integer next : list[arr[i]]) {//内循环表示从该节点向外蔓延
                if (!isVisited[next]){
                    isVisited[next] = true;
                    dfs(next,cur+1);
                    isVisited[next] = false;
                }
            }
        }
    }

    /**
     * 求和计算，判断当前路径是否已存在
     * @param cur 下标
     */
    private static boolean check(int cur){
        int ans = 0;
        for (int i = 0; i <= cur; i++) {
            ans += (1 << arr[i]);
        }
        if (isCheck[ans]) return true;//如果当前路径已经存在过
//        System.out.println(Arrays.toString(arr)+"   "+cur);
        cnt++;
        isCheck[ans] = true;
        return false;
    }

    private static void add(int i,int j){
        list[i].add(j);
        list[j].add(i);
    }
}