多项式计算详解：从NTT到指数与对数-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_54026781/article/details/127946990

本文深入探讨了多项式的各种计算方法，包括点值表示法、原根的概念及其性质、蝴蝶变换、快速傅里叶变换(NTT)、多项式求逆、开方、指数和对数运算。通过这些理论和算法，可以高效地处理模数环境下的多项式操作，并提供了相应的代码实现模板。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1.点值表示法

点值表示法是多项式的另一种表示方法，多项式一般是用表达式表示，对于一个n次的多项式我们可以代入n+1个点来确定这个多项式。
假设A(x)=a0+a1x+a2x²+a3x³…+anxⁿ
这n+1个点确定了这个多项式A（x）
换句话说A这个数唯一地对应了这n+1个点的集合，根据这n+1个点的集合也能反推出A。这种表示方法叫点值表示法

2.原根

定义：
假设一个数g是P的原根，那么gⁱ mod P的结果两两不同，且有 1<g<P，0<i<P，归根到底就是g^(P-1) ≡ 1 (mod P)当且仅当指数为P-1的时候成立.(这里P是素数)。

阶的定义
设m>1,gcd(a,m)=1,使得
成立的最小的r，称为a对模m的阶。
性质：
1.对于正整数m，只有当m=2，4，q^a,
2q^a 时m才有原根（q为奇素数，a≥1）
2.然后呢对于m的原根g，g^i(mod p)（0<=i<=p-2）的值两两不相同，且在[0,p-2]内
常见模数的原根
998244353，1004535809的原根为3
为什么原根能用
FFT中使用的单位根，可以被替换成原根，原根也具有相类似的性质，我们设g为p的原根,令g(N)=g^((p-1)/N),要求p-1能被N整除
性质1 g(N)^N≡1(mod p)
性质2 g(N)^N/2≡-1(mod p)
性质3 g(2N)^2*k≡ g(N)^K(mod p)
性质4 g(N)^k+N/2≡-g(N)^k(mod p）
可见单位根有的性质原根也有，所以我们可以用原根替换单位根来解决计算过程中有模数的问题

3.蝴蝶变换

如果使用递归实现的话会有很大的常数，遇到有些卡常题会TLE，是因为不断复制数组和每次都要排序而导致的，所以我们可以一开始就把最终的位置算出来，然后进行倍增合并，这样常数省下来了，且代码也更好写一点，这个合并的过程就叫做蝴蝶变换
那么如何快速得到每个数最后在那个位置呢？
打印几个结果后，发现是有规律的，规律就是每个数最后位置的下标等于当前下表的二进制的翻转
列如6的二进制为(110),翻转后为(011),所以下标为6的数最后会在下标为3的位置上，这样我们就可以O(n)的得到最终的数列了

void change(ll y[],ll len)
{
   
    int i,j,k;//cout<<i<<" "<<j<<endl;;
    for(int i=1,j=len/2; i<len-1; i++)
    {
   
        if(i<j)swap(y[i],y[j]);
        int k=len/2;
        while(j>=k)
        {
   
            j-=k;
            k=k/2;
        }
        j+=k;
    }
}

4.NTT实现(O(nlogn))

所以只需要把FFT中的单位根换成原根就可以了,然后计算全部在取模的环境下就可以了
DFT 在这里插入图片描述
IDFT

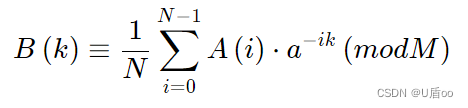
a是原根，a^-ik是代表在mod M下的逆元
模板题
代码实现

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const long double PI = acos(-1.0);
const ll p=998244353;//模数
const ll G=3;//原根
typedef long long ll;
typedef long double db;
ll ksm(ll a,ll b)
{
   
    ll ans=1;
    while(b)
    {
   
        if(b&1)ans=ans*a;
        a=a*a;
        b=b>>1;
    }
    return ans;
}
void change(ll y[],ll len)
{
   
    int i,j,k;//cout<<i<<" "<<j<<endl;;
    for(int i=1,j=len/2; i<len-1; i++)
    {
   
        if(i<j)swap(y[i],y[j]);
        int k=len/2;
        while(j>=k)
        {
   
            j-=k;
            k=k/2;
        }
        j+=k;
    }
}
void ntt(ll y[], int len, int on)
{
   
    change(y, len);
    for (int h = 2; h <= len; h <<= 1)
    {
   
        ll wn=ksm(G,(p-1)/h);
        if(on==-1)
        {
   
            wn=ksm(wn,p-2);
        }
        for (int j = 0; j < len; j += h)
        {
   
            ll w=1;
            for (int k = j; k < j + h / 2; k++)
            {
   
                ll u = y[k]%p;
                ll t = w * y[k + h / 2]%p;
                y[k] = (u + t)%p;
                y[k + h / 2] = (u - t+p)%p;
                w = (w * wn)%p;
            }
        }
    }
    if (on == -1)
    {
   
        ll len_inv = ksm(len,p-2);//N的逆元（N是limit, 指的是2的整数幂）
        for(int i = 0; i < len; ++ i)
            y[i] = (y[i] * len_inv) % p;//NTT还是要除以n的，但是这里把除换成逆元了，inv就是n在模p意义下的逆元
    }
}
ll a[4000010],b[4000010];
void prepare(int len1, int len2)
{
   
    int c=1;
    while(c<(max(len1,len2))*2)c=c<<1;
    // cout<<c<<endl;
    for(int i=len1; i<c; i++)a[i]=0;
    for(int i=len2; i<c; i++)b[i]=0;
    ntt(a,c,1);
    ntt(b,c,1);
    //cout<<1<<endl;
    for(int i=0; i<c; i++)a[i]=a[