深度学习.

目录

深度学习是什么?

神经网络

1.神经网络任务

2.神经网络的输入

3.神经网络的输出

深度学习任务

神经元

如何找一个函数？

梯度下降

Loss函数

线性函数和多层神经元

---

深度学习是什么?

        深度学习是机器学习的一个子集：利用多层神经网络从大量数据中进行学习。即设计一个很深的网络架构让机器自己学。深度学习本质上就是找一个函数f的过程。x通过函数f映射到y。

神经网络

1.神经网络任务

        输入的数据x，通过神经网络f 映射后，再输出y。如：

                f （                   x               ）  =       y         

                f （    身高，体重，财富    ）  =   寿命        

                f （      动漫人物的图片      ）  =    人物名字    

                f （              “描述”             ）  =    图片              

2.神经网络的输入

        一般有三种数据形式：向量、矩阵/张量、序列

        为什么说一张图片是由矩阵组成的？

        我们都知道，图片的像素点是由R、G、B三色混合组成的。假设有一张100x100像素点的图片，每个像素点有R、G、B三通道，所以一张图片就是矩阵。

        序列：是一种有序的组织方式，使事物之间有了明确的先后关系。例如：“我用的苹果”和“我吃的苹果”这两句话中的“苹果”的含义不相同。视频就是典型的序列，因为视频是由一帧一帧图片组成。不同的图片排放顺序可以构成不同的视频。

3.神经网络的输出

输出一般有以下三种类别：

1）回归任务（填空题）：所谓的回归任务就是猜一个数，例如：根据以前的温度推测明天的温度大概有多高

2）分类任务（选择题）：例如有A、B、C、D四个选项，在这四个选项中选一个

                                           图片：猫 / 狗                           从猫 / 狗中选一个

                                           句子：积极 / 消极                    从积极 / 消极中选一个

                                            疾病：轻度 / 中度 / 重度         从轻度 / 中度 / 重度选一个

3）生成任务（结构化）（填空题）：例如ChatGpt生成文本、图片。所有的结构化输出都是用类似于分类的方式实现的。

小练习：判断每个任务的输入和输出分别是什么？

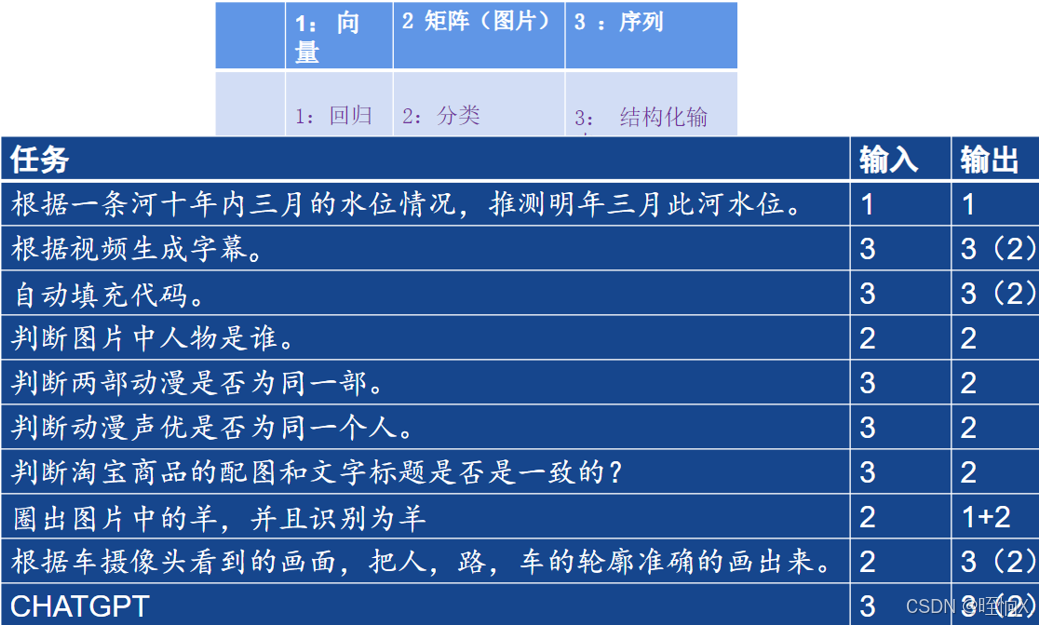
深度学习任务

分类和回归是结构化的基础。

分类时，是用数字来表示类别。

有的时候需要多个模态（模态：例如有图有数据的任务）的数据，比如图片，文字，声音都是不同的模态。

神经元

在了解了输入和输出，来谈谈神经元：

大家都说深度学习需要数据，这是为什么？因为要从数据中找到函数。那么如何从数据中找到想要的函数：

        1.定义一个函数（模型）

        2.定义一个合适的损失函数

        3.根据损失，对模型进行优化

我们自己先定义一个函数f' ，此时的函数f'和真实的函数f存在差距。我们的目标是要让f'尽可能的靠近真实函数f。定义一个合适的损失函数（loss函数），用来衡量定义的函数f'和真实函数f之间的差值有多大。根据损失（差值）对模型进行优化，通过数据一步一步更新，使得模型越来越靠近真实函数，最后得到真实函数。

如何找一个函数？

例：

小车的车速V=初速度V0 + 加速度a + 时间 t
x（数据feature）	y=2x+1+ε   （标签label）
1	3.1
2	5.1
3	6.9
4	8.7
5	10.8
6	13.5
7	？

怎么从前6组数据，推断出第7组数据的y值，这就需要从中总结出函数。那么该怎么总结呐？实际上就是上面说的那三步：

        1.定义一个函数：根据上述的y值，推测可能是线性模型（Linear Model），因此定义 ŷ=wx+b。这个函数就是我们的模型，ŷ是预测值，w是weight（权重），b是bias（偏差）。权重和偏差都是未知参数。

        2.定义一个合适的损失函数：

                Loss function of unknown para : L(w,b)=| ŷ -y | = | wx+b-y |

                Loss就是这些未知参数的函数

                Loss：判断我们选择的这组参数怎么样

            若不好理解，我们给定w0=3 ， b0=2 , 即：ŷ=3x+2

x（数据feature）	y=2x+1+ε   （标签label）	ŷ=3x+2	loss
1	3.1	5	1.9
2	5.1	8	2.9
3	6.9	11	4.1
4	8.7	14	5.3
5	10.8	17	6.2
6	13.5	20	6.5
7	？		4.48

把x=1，2，....，6分别带入到ŷ=3x+2，算出值，并用 | ŷ-y | 算出loss值，结果如上表。

通过前6组数据的loss值，我们可以预测x=7时的Loss值，可由   得出:

即L=(1.9+2.9+4.1+5.3+6.2+6.5) / 6 = 4.48 ，这个Loss值就衡量了w0=3，b0=2这组数字选的好不好，显然数字太大了，选取的不好。

        3.根据损失，对模型进行优化

         优化公式：       这个公式的含义是，w*，b*是让Loss最小的w，b

对于本例，L和W之间的关系如上图，优化的方法：梯度下降。

梯度下降

那么又该如何进行梯度下降：

1.

2.  

        如果导数是正的，说明左低右高，左边loss值小，右边loss值大，w要往左挪，使梯度变小。

w要挪动多少呐？

learning rate是学习率，是超参数（人为规定的，机器无法学习的）

3.

需要注意：上述L是关于w，b的函数，即L(w，b)=| ŷ -y | = | wx+b-y |

在优化过程中，对b的操作也是一样的，总结如下：

Loss函数

值得注意的是loss函数并不一定都是绝对值的形式.

上述的loss函数是MAE（Mean Absolute Error）：L（w，b）=| ŷ -y |       （均绝对误差）

还有MSE（Mean Square Error）：L（w，b）=|（ ŷ -y ）^2       （均误差）

像这样的loss函数还有很多，只要能够很好的衡量 ŷ -y 之间的差距，那就是一个好的loss函数

线性函数和多层神经元

神经元：，它背后的数学公式就是ŷ=wx+b，

一个个这样的神经元就可以组成多层神经元。

值得注意的是：这样的线性公式只能画出一条直线，即它没办法只画一条直线，把下图的三角形和正方形分开，而它又无法画出下图的圈。

线性函数也无法画出下图的分段函数，这是线性函数的缺点，而激活函数可以实现。

关于激活函数的内容，可移步（深度学习——多层神经网络-优快云博客）查看