机器学习与数据挖掘-实验二

1. 根据给定数据集（存放在data1.txt文件中，二分类数据），编码实现基于梯度下降的Logistic回归算法，画出决策边界；

2. 从UCI中选择鸢尾花数据集（多分类数据），使用Sklearn实现Logistic回归；

实现第一个决策边界的代码如下：（注意格式）

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.metrics import accuracy_score
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression

data=np.array(pd.read_csv('data1.txt'))
t=data[:,2]
data=data[:,:2]
#1. 根据给定数据集（存放在data1.txt文件中，二分类数据），编码实现基于梯度下降的Logistic回归算法，画出决策边界；
def plotDescisionBoundary(X,Y):
    #逻辑回归模型
    lr = LogisticRegression(C=1e5)  
    lr.fit(X,Y)
    #meshgrid函数生成两个网格矩阵
    h = .02
    x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
    y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    #pcolormesh函数将xx,yy两个网格矩阵和对应的预测结果Z绘制在图片上
    Z = lr.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    plt.figure(1, figsize=(8,6))
    plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)
    #绘制散点图,将数据按0和1分类
    n = data.shape[0]
    xcord1 = []; ycord1 = []
    xcord2 = []; ycord2 = []
    for i in range(n):
        if int(t[i])== 1:
            xcord1.append(data[i,0]); ycord1.append(data[i,1])
        else:
            xcord2.append(data[i,0]); ycord2.append(data[i,1])
    
    plt.scatter(xcord1, ycord1, color='green',marker='o',label='1')
    plt.scatter(xcord2, ycord2, color='red', marker='x',label='0')
    plt.xlabel('x',color='black',fontsize=20)
    plt.ylabel('y',color='black',fontsize=20)
    plt.xlim(xx.min(), xx.max())
    plt.ylim(yy.min(), yy.max())
    plt.xticks(())
    plt.yticks(())
    plt.legend(loc=2) 
    plt.show()
    plt.title('决策分界',color='red',fontsize=20)

plotDescisionBoundary(data,t)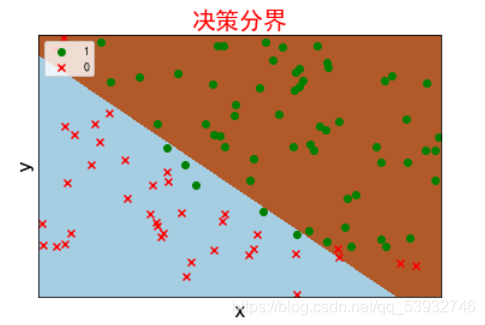

莺尾花的代码如下：（注意格式）

import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.metrics import accuracy_score
from sklearn.datasets import load_iris
iris = load_iris()
X1 = iris.data[:, 0:2]
X2 = iris.data[:, 1:3]
X3 = iris.data[:, 2:4]
Y = iris.target
def plotDescisionBoundary(X,Y):
    #逻辑回归模型
    lr = LogisticRegression(C=1e5)  
    lr.fit(X,Y)
    #meshgrid函数生成两个网格矩阵
    h = .02
    x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
    y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    #pcolormesh函数将xx,yy两个网格矩阵和对应的预测结果Z绘制在图片上
    Z = lr.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    plt.figure(1, figsize=(8,6))
    plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)
    #绘制散点图
    plt.scatter(X[:50,0], X[:50,1], color='red',marker='o', label='setosa')
    plt.scatter(X[50:100,0], X[50:100,1], color='blue', marker='x', label='versicolor')
    plt.scatter(X[100:,0], X[100:,1], color='green', marker='s', label='Virginica') 
    plt.xlabel('Sepal length',color='black',fontsize=15)
    plt.ylabel('Sepal width',color='black',fontsize=15)
    plt.xlim(xx.min(), xx.max())
    plt.ylim(yy.min(), yy.max())
    plt.xticks(())
    plt.yticks(())
    plt.legend(loc=2) 
    plt.show()
    plt.title('决策分界',color='red',fontsize=20)

plotDescisionBoundary(X1,Y)
plotDescisionBoundary(X2,Y)
plotDescisionBoundary(X3,Y)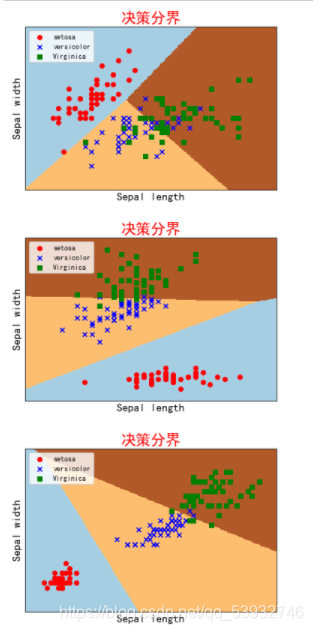

基于莺尾花数据集实现梯度下降，画出决策边界

import numpy as np
import matplotlib.pyplot as plt
from sklearn import linear_model
from sklearn.metrics import accuracy_score
from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression

plt.rcParams['font.sans-serif']='SimHei'
plt.rcParams['axes.unicode_minus']=False
iris = load_iris()
X = iris.data[:, :2]
Y = iris.target
def plotDescisionBoundary(X,Y):
    #逻辑回归模型
    lr = LogisticRegression(C=1e5)  
    lr.fit(X,Y)
    #meshgrid函数生成两个网格矩阵
    h = .02
    x_min, x_max = X[:, 0].min() - .5, X[:, 0].max() + .5
    y_min, y_max = X[:, 1].min() - .5, X[:, 1].max() + .5
    xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
    #pcolormesh函数将xx,yy两个网格矩阵和对应的预测结果Z绘制在图片上
    Z = lr.predict(np.c_[xx.ravel(), yy.ravel()])
    Z = Z.reshape(xx.shape)
    plt.figure(1, figsize=(8,6))
    plt.pcolormesh(xx, yy, Z, cmap=plt.cm.Paired)
    #绘制散点图
    plt.scatter(X[:50,0], X[:50,1], color='red',marker='o', label='setosa')
    plt.scatter(X[50:100,0], X[50:100,1], color='blue', marker='x', label='versicolor')
    plt.scatter(X[100:,0], X[100:,1], color='green', marker='s', label='Virginica') 
    plt.xlabel('Sepal length',color='black',fontsize=15)
    plt.ylabel('Sepal width',color='black',fontsize=15)
    plt.xlim(xx.min(), xx.max())
    plt.ylim(yy.min(), yy.max())
    plt.xticks(())
    plt.yticks(())
    plt.legend(loc=2) 
    plt.show()
    plt.title('决策分界',color='red',fontsize=20)

plotDescisionBoundary(X,Y)

编程实现10折交叉验证法，估计对数回归的错误率

import numpy as np
import pandas as pd
import sklearn
from sklearn.linear_model import LogisticRegression
from sklearn import model_selection
from sklearn.model_selection import cross_val_predict

log_model=LogisticRegression()
data=load_iris()
x=data.data
y=data.target
# 十折交叉验证生成训练集和测试集
def tenfolds():
    k = 0
    truth = []
    while k < 10:
        kf = model_selection.KFold(n_splits=10, random_state=None, shuffle=True)
        for x_train_index, x_test_index in kf.split(data.data):
            x_train = data.data[x_train_index]
            y_train = data.target[x_train_index]
            x_test = data.data[x_test_index]
            y_test = data.target[x_test_index]
        # 用对率回归进行训练，拟合数据
        log_model = LogisticRegression(multi_class= 'ovr', solver = 'liblinear')
        log_model.fit(x_train, y_train)
        # 用训练好的模型预测
        y_pred = log_model.predict(x_test)
        for i in range(15):
            if y_pred[i] == y_test[i]:
                truth.append(y_pred[i] == y_test)
        k += 1
    # 计算精度
    accuracy = len(truth)/150
    print("用10折交叉验证对率回归的精度是：", accuracy)
    print("用10折交叉验证对率回归的错误率是：", 1-accuracy)
    
tenfolds()