蓝桥杯练习（【思特奇杯·云上蓝桥-算法集训营】第2周）

第一题：带分数

问题描述

100 可以表示为带分数的形式：100 = 3 + 69258 / 714。

还可以表示为：100 = 82 + 3546 / 197。

注意特征：带分数中，数字1~9分别出现且只出现一次（不包含0）。

类似这样的带分数，100 有 11 种表示法。

输入格式

从标准输入读入一个正整数N (N<1000*1000)

输出格式

程序输出该数字用数码1~9不重复不遗漏地组成带分数表示的全部种数。

注意：不要求输出每个表示，只统计有多少表示法！

样例输入1

100

样例输出1

11

样例输入2

105

样例输出2

6

代码：

#include <iostream>
#include <string>
#include <cstdlib>
#include <algorithm>

using namespace std;

int parse(const char* arr, int pos, int len) {
    int ans = 0;
    int t = 1;
    for (int i = pos + len - 1; i >= pos; --i) {
        ans += (arr[i] - '0') * t;
        t *= 10;
    }
    return ans;
}

int main() {
    int n=0, ans = 0;
    cin >> n;
    string s = "123456789";
    do {
        const char* str = s.c_str();//c_str会返回一个const
        for (int i = 1; i <= 7; ++i) {//+号前的串长度
            int inta = parse(str, 0, i);
            if (inta >= n) break;
            for (int j = i; j <= 9 - i - 1; ++j) {//+/两个符号之间的串长度
                int intb = parse(str, i, j);
                int intc = parse(str, i + j, 9 - i - j);
                if (intb % intc == 0 && inta + intb / intc == n) ans++;
            }
        }
    } while (next_permutation(s.begin(), s.end()));
    printf("%d\n", ans);
    return 0;
}

第二题：李白打酒

题目描述

话说大诗人李白，一生好饮。幸好他从不开车。

一天，他提着酒壶，从家里出来，酒壶中有酒2斗。他边走边唱：

无事街上走，提壶去打酒。

逢店加一倍，遇花喝一斗。

这一路上，他一共遇到店5次，遇到花10次，已知最后一次遇到的是花，他正好把酒喝光了。

请你计算李白遇到店和花的次序，可以把遇店记为a，遇花记为b。则：babaabbabbabbbb 就是合理的次序。像这样的答案一共有多少呢？请你计算出所有可能方案的个数（包含题目给出的）。

代码：

#include <iostream>
#include <algorithm>
using namespace std;


int main()
{
	
	int time = 0;
	int arr[15] = {-1,-1, -1, -1, -1, -1, -1, -1,-1, -1, 2 , 2 , 2 , 2, 2 };
	do {
		int  n = 2;
		for (int i = 0;i < 15;i++)
		{
			if (arr[i] == -1) {
				n += arr[i];
			}
			else {
				n *= arr[i];
			}
		}

		if (arr[14] == -1 && n == 0)
			time += 1;
	} while (next_permutation(arr, arr + 15)); //全排列

	cout << time<< endl;
	return 0;
}

 

 

第三题：第39级台阶

题目描述：

    小明刚刚看完电影《第39级台阶》，离开电影院的时候，他数了数礼堂前的台阶数，恰好是39级!

    站在台阶前，他突然又想着一个问题：

    如果我每一步只能迈上1个或2个台阶。先迈左脚，然后左右交替，最后一步是迈右脚，也就是说一共要走偶数步。那么，上完39级台阶，有多少种不同的上法呢？

输出格式：

输出一个整数

代码：

#include <iostream>
 
using namespace std;
int num = 0;
void fun(int m ,int step) {
    if (m < 0) return;  
    if (m == 0) {
        if (step % 2 == 0) num++;
        return;
    }
    fun(m - 1, step + 1);
    fun(m - 2, step + 1);
}
int main()
{
    int step = 39;
    fun(39, 0);
    cout << num << endl;
    return 0;
}

//答案：51167078

 

第四题：穿越雷区

题目描述

已知的地图是一个方阵，上面用字母标出了A，B区，其它区都标了正号或负号分别表示正负能量辐射区。

例如：

A + - + -

- + - - +

- + + + -

+ - + - +

B + - + -

坦克车只能水平或垂直方向上移动到相邻的区。

数据格式要求：

输入第一行是一个整数n，表示方阵的大小， 4<=n<100

接下来是n行，每行有n个数据，可能是A，B，+，-中的某一个，中间用空格分开。

A，B都只出现一次。

要求输出一个整数，表示坦克从A区到B区的最少移动步数。

如果没有方案，则输出-1

例如：

用户输入：

5

A + - + -

- + - - +

- + + + -

+ - + - +

B + - + -

则程序应该输出：

10

代码：

#include <iostream>
#include <stdlib.h>
using namespace std;

int num = 0;
void search(char a[100][100], int n) {
	int ai = 0, aj = 0, bi = 0, bj = 0;
	for (int i = 0;i < n;i++)
	{
		for (int j = 0; j < n;j++)
		{
			if (a[i][j] == 'A') {
				ai = i;
				aj = j;
			}
			if (a[i][j] == 'B') {
				bi = i;
				bj = j;
			}
		}
	}
	num = abs(ai - bi) + abs(aj - bj);
}
int main()
{
	int n =4;
	char a[100][100]{};
	char m;
	cin >> n;
	for (int i = 0;i < n;i++)
	{
		for (int j = 0; j < n;j++)
		{
			cin >> m;
		}
	}

	search(a, n);
	return 0;

}

 

第五题：迷宫

题目描述

下图给出了一个迷宫的平面图，其中标记为 1 的为障碍，标记为 0 的为可 以通行的地方。

010000

000100

001001

110000

迷宫的入口为左上角，出口为右下角，在迷宫中，只能从一个位置走到这 个它的上、下、左、右四个方向之一。 对于上面的迷宫，从入口开始，可以按DRRURRDDDR 的顺序通过迷宫， 一共 10 步。其中 D、U、L、R 分别表示向下、向上、向左、向右走。 对于下面这个更复杂的迷宫（30 行 50 列），请找出一种通过迷宫的方式， 其使用的步数最少，在步数最少的前提下，请找出字典序最小的一个作为答案。 请注意在字典序中D<L<R<U。（如果你把以下文字复制到文本文件中，请务 必检查复制的内容是否与文档中的一致。在试题目录下有一个文件 maze.txt， 内容与下面的文本相同）

答案提交

这是一道结果填空的题，你只需要算出结果后提交即可。本题的结果为一 个字符串，包含四种字母 D、U、L、R，在提交答案时只填写这个字符串，填 写多余的内容将无法得分

 代码：

#include<iostream>
#include<cstdio>
#include<cstring>
#include<string>
#include<cmath>
#include<cstdlib>
#include<algorithm> 
#include<queue>
using namespace std;
typedef long long ll;
#define PI 3.1415927
#define M(a) memset(a,0,sizeof(a))
const int INF = 0x3f3f3f3f;
int dir[30][50] = { {1,0},{0,-1},{0,1},{-1,0} }, vis[30][50];
string S = "DLRU";
char mazz[30][50];
struct node {
	int x, y, step;
	string str;
	node(int x1, int y1, string s1, int st1)
	{
		x = x1, y = y1, str = s1, step = st1;
	}
};

int test(int x, int y)
{
	return mazz[x][y] == '1' || x < 0 || x >= 30 || y < 0 || y >= 50 || vis[x][y] == 1 ? 0 : 1;
}

void bfs(int x, int y, string s, int step)
{
	queue<node> q;
	q.push(node(x, y, s, step));
	while (!q.empty())
	{
		node top = q.front();
		q.pop();
		if (top.x == 29 && top.y == 49)
		{
			cout << top.str << top.step;
			return;
		}
		for (int i = 0;i < 4;i++)
		{
			int tx = top.x + dir[i][0];
			int ty = top.y + dir[i][1];
			if (test(tx, ty))
			{
				q.push(node(tx, ty, top.str + S[i], top.step + 1));
				vis[tx][ty] = 1;
			}
		}
	}
}

int main()
{
	for (int i = 0;i < 30;i++)
		cin >> mazz[i];
	bfs(0, 0, "", 0);
	return 0;
}

 

 

 第六题：跳马

题目描述：

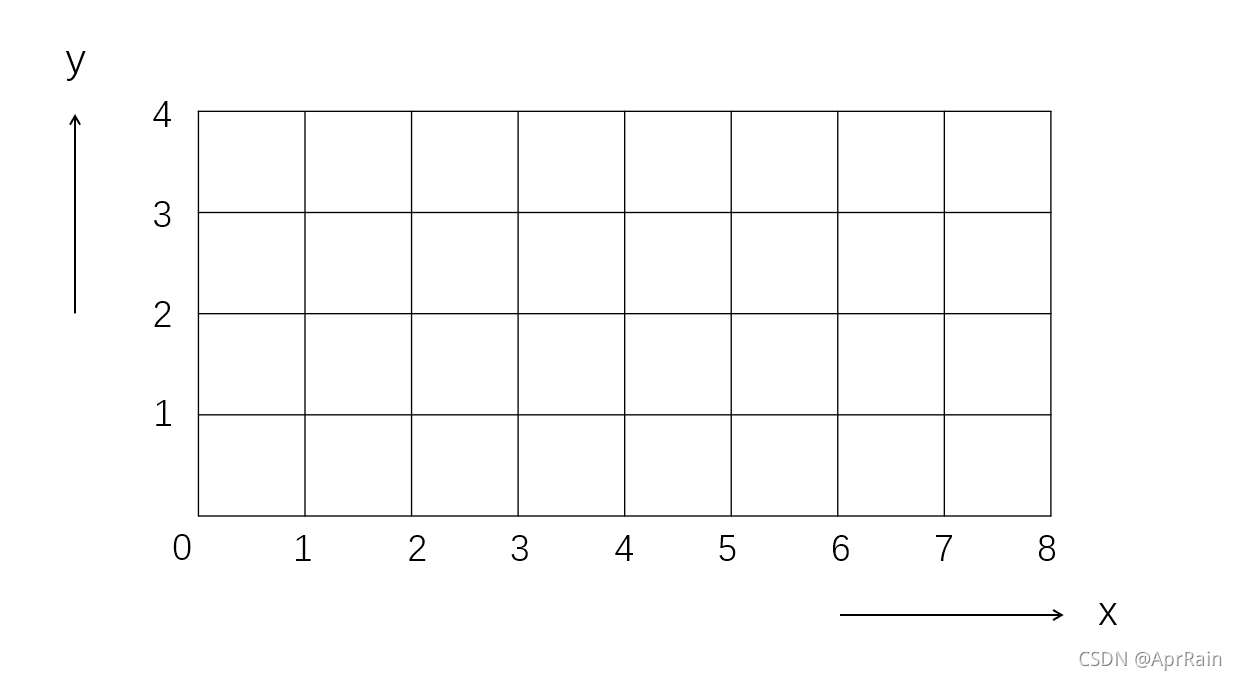
在半张中国象棋的棋盘上，一匹马从左下角跳到右上角，只允许往右跳，不允许往左跳，问有多少种方案。

中国象棋的棋盘是 8×8 格规模大小，半张棋盘就是 8×4 格规模大小，如图所示。由题意得棋子要从 (0,0) 位置走到 (8,4) 位置。取值范围 0≤x≤8，0≤y≤4。

 

代码：

#include<iostream>
using namespace std;

int ax[9], ay[9];
int dir[4][2] = { {1,2},{1,-2},{2,1},{2,-1} };
int c = 0;

bool inMap(int x, int y) {
    return x >= 0 && x <= 8 && y >= 0 && y <= 4;
}

void output(int n) {
    cout << "0 0"; 
    for (int i = 1;i <= n;i++) {
        cout << " → " << ax[i] << " " << ay[i];
    }
    cout << endl;
}

void findRoad(int n) {
    int x1 = ax[n], y1 = ay[n]; 
    if (x1 == 8) { 
        if (y1 == 4) { 
            output(n);
            c ++;
        }
    }
    for (int i = 0;i < 4;i++) { 
        int x2 = x1 + dir[i][0];
        int y2 = y1 + dir[i][1]; 
        if (inMap(x2, y2)) {
            ax[n + 1] = x2; 
            ay[n + 1] = y2; 
            findRoad(n + 1);  
        }
    }
}

int main() {
    findRoad(0); 
    cout << "共有" << c << "种方案！" << endl;
    return 0;
}

 

第七题：路径之谜

题目描述：

小明冒充X星球的骑士，进入了一个奇怪的城堡。

城堡里边什么都没有，只有方形石头铺成的地面。

假设城堡地面是 n x n 个方格。【如图1.png】所示。

按习俗，骑士要从西北角走到东南角。

可以横向或纵向移动，但不能斜着走，也不能跳跃。

每走到一个新方格，就要向正北方和正西方各射一箭。

（城堡的西墙和北墙内各有 n 个靶子）

同一个方格只允许经过一次。但不必做完所有的方格。

如果只给出靶子上箭的数目，你能推断出骑士的行走路线吗？

有时是可以的，比如图1.png中的例子。

本题的要求就是已知箭靶数字，求骑士的行走路径（测试数据保证路径唯一）

输入：

第一行一个整数N(0<N<20)，表示地面有 N x N 个方格

第二行N个整数，空格分开，表示北边的箭靶上的数字（自西向东）

第三行N个整数，空格分开，表示西边的箭靶上的数字（自北向南）

输出：

一行若干个整数，表示骑士路径。

为了方便表示，我们约定每个小格子用一个数字代表，从西北角开始编号: 0,1,2,3....

比如，图1.png中的方块编号为：

0  1  2  3

4  5  6  7

8  9  10 11

12 13 14 15

示例：

用户输入：

4

2 4 3 4

4 3 3 3

程序应该输出：

0 4 5 1 2 3 7 11 10 9 13 14 15

代码：

#include <iostream>
#include <vector>
#include <cstring>
using namespace std;
int north[25], west[20], mp[25][25], mark[25][25];
int n;
int d[4][2] = { {0,1},{0,-1},{1,0},{-1,0} };
vector<int> way;
void dfs(int x, int y)
{
	if (x == n - 1 && y == n - 1)//如果到达终点
	{
		int cntX[25], cntY[25];
		memset(cntX, 0, sizeof(cntX));
		memset(cntY, 0, sizeof(cntY));
		for (int i = 0;i < n;i++)
			for (int j = 0;j < n;j++)
			{
				cntX[i] += mark[i][j];
				cntY[j] += mark[i][j];
			}
		int flag = true;
		for (int i = 0;i < n;i++)
		{
			if (cntX[i] != west[i])
			{
				flag = false;
				break;
			}
		}
		for (int i = 0;i < n;i++)
		{
			if (cntY[i] != north[i])
			{
				flag = false;
				break;
			}
		}
		if (flag)
		{
			for (int i = 0;i < way.size();i++)
			{
				if (i == 0)
					cout << way[i];
				else
					cout << " " << way[i];
			}
		}
	}
	int tx, ty;
	for (int i = 0;i < 4;i++)
	{
		tx = x + d[i][0];
		ty = y + d[i][1];
		if (tx >= 0 && tx < n && ty >= 0 && ty < n && mark[tx][ty] == 0)
		{
			mark[tx][ty] = 1;
			way.push_back(mp[tx][ty]);
			dfs(tx, ty);
			mark[tx][ty] = 0;
			way.pop_back();
		}
	}
}
int main()
{
	cin >> n;
	for (int i = 0;i < n;i++)
		cin >> north[i];
	for (int i = 0;i < n;i++)
		cin >> west[i];
	int t = 0;
	for (int i = 0;i < n;i++)
		for (int j = 0;j < n;j++)
			mp[i][j] = t++;//给格子编码
	mark[0][0] = 1;
	way.push_back(0);
	dfs(0, 0);
}


//样例输入：
//4
//2 4 3 4
//4 3 3 3

//样例输出：
// 0 4 5 1 2 3 7 11 10 9 13 14 15

 

第八题：未名湖边的烦恼

问题描述：

　　每年冬天，北大未名湖上都是滑冰的好地方。北大体育组准备了许多冰鞋，可是人太多了，每天下午收工后，常常一双冰鞋都不剩。

　　每天早上，租鞋窗口都会排起长龙，假设有还鞋的m个，有需要租鞋的n个。现在的问题是，这些人有多少种排法，可以避免出现体育组没有冰鞋可租的尴尬场面。（两个同样需求的人（比如都是租鞋或都是还鞋）交换位置是同一种排法）

输入格式

　　两个整数，表示m和n

输出格式

　　一个整数，表示队伍的排法的方案数。

样例输入

3 2

样例输出

5

数据规模和约定

m,n∈［0,18］

 代码：

#include <iostream>

using namespace  std;

int fun(int m, int n) {
    if (m < n) return 0;
    else if (n == 0) return 1;
    else return fun(m - 1, n) + fun(m, n - 1);
}
int main()
{
    int m= 0, n=0;
    cin >> m >> n;
    cout << fun(m, n);
    return 0;
}

 

第十题：2n皇后问题

题目描述：

给定一个n*n的棋盘，棋盘中有一些位置不能放皇后。现在要向棋盘中放入n个黑皇后

和n个白皇后，使任意的两个黑皇后都不在同一行、同一列或同一条对角线上，任意的两

个白皇后都不在同一行、同一列或同一条对角线上。问总共有多少种放法？n小于等于8。

输入格式：

输入的第一行为一个整数n，表示棋盘的大小。

接下来n行，每行n个0或1的整数，如果一个整数为1，表示对应的位置可以放皇后，

如果一个整数为0，表示对应的位置不可以放皇后。

输出格式：

输出一个整数，表示总共有多少种放法。

案例输入

No.1

4

1 1 1 1

1 1 1 1

1 1 1 1

1 1 1 1

No.2

4

1 0 1 1

1 1 1 1

1 1 1 1

1 1 1 1

案例输出

No.1

2

No.2

0

 代码：

#include <iostream>
#include <cstdio>
#include <cmath>
using namespace std;

int n ,ans;
int a[10][10];//棋盘
int white[10], black[10];

int valid_white(int row, int conlumn)
{
    for (int i = 1;i < row; i++)
        if (conlumn == white[i] || abs(row - i) == abs(conlumn - white[i]))
            return 0;
    return 1;
}

int valid_black(int row, int conlumn) {
    for (int i = 1;i < row;i++) {
        if (conlumn == black[i] || abs(row - i) == abs(conlumn - black[i]))
            return 0;
    }
    return 1;
}

void queen_black(int row) {
    if (row == n + 1) {
        ans++;
    }
    else {
        for (int i = 1;i <= n;i++) 
            if (a[row][i] == 0 || i == white[row])
                continue;
            else if (valid_black(row, i)) {
                black[row] = i;
                queen_black(row + 1);
            }
    }
}

void queen_white(int row) {
    if (row == n + 1) {
        queen_black(1);
        return;
    }
    else {
        for (int i = 1;i <= n;i++) 
            if (a[row][i] == 0 )
                continue;
            else if (valid_white(row, i)) {
                white[row] = i;
                queen_white(row + 1);
            }
        
    }
}

int main()
{
    cin >> n;
    for (int i = 1;i <= n;i++) {
        for (int j = 1;j <= n;j++) {
            cin >> a[i][j];
        }
    }
    queen_white(1);
    cout << ans;
    return 0;
}