2024考研 自命题树的相关代码题操作（自用可执行代码）

已于 2023-11-08 15:56:56 修改
阅读量238 收藏 4
点赞数
文章标签： 算法
于 2023-11-06 15:06:39 首次发布
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_53631431/article/details/133419518
版权

1.层次建树的相关操作

       "function.h"的头文件引用
#include <stdio.h>
#include <stdlib.h>

typedef char ElemType;

typedef struct BiTNode {//树的结构体
	char data;//数据域
	BiTNode* rchild;//右孩子
	BiTNode* lchild;//左孩子
}BiTNode, * BiTree;

typedef struct tag {//建立一个辅助队列
	BiTree p;//树的某一个结点的地址值
	struct  tag* pnext; //辅助队列的指针节点
}tag_t, * ptag_t;
         层次建树的代码操作
                主函数main的代码内容
int main() {
	BiTree pnew; //用来申请一个树的新节点
	BiTree tree = NULL;//指向树根的一个节点
	char c;
	ptag_t phead = NULL, ptail = NULL, listpnew = NULL, pcur = NULL;//建立辅助队列的相关节点
	while (scanf_s("%c", &c))
	{
		if (c == '\n') {
			break;
		}
		//calloc申请的空间大小
		pnew = (BiTree)calloc(1, sizeof(BiTNode));//calloc对申请空间进行初始化
		pnew->data = c;//数据放入
		listpnew = (ptag_t)calloc(1, sizeof(tag_t));//给辅助队列节点申请节点空间
		listpnew->p = pnew;
		//如果是树的第一个节点
		if (tree == NULL) {
			tree = pnew;//指向树根节点
			phead = listpnew; //第一个节点既是队列头又是队列尾
			ptail = listpnew;
			pcur = listpnew;//指向进入树的父亲元素
			continue;
		}
		else
		{
			//让元素先入队列
			ptail->pnext = listpnew;
			ptail = listpnew;
		}
		if (pcur->p->lchild == NULL) {
			pcur->p->lchild = pnew;
		}
		else if (pcur->p->rchild == NULL)
		{
			pcur->p->rchild = pnew;//将新节点插入到结点的右边
			pcur = pcur->pnext;//向后移动左右孩子都已经满了
		}
	}

	printf("-------前序遍历-----------------\n");
	PreOrder(tree);
	printf("\n-------中序遍历-----------------\n");
	InOrder(tree);
	printf("\n-------后序遍历-----------------\n");
	PostOrder(tree);
	return 0;
}
        前中后遍历函数的代码内容
void visit(BiTree p) {
	printf("%c", p->data);
}//打印


void PreOrder(BiTree p) {
	if (p != NULL) {
		visit(p);
		PreOrder(p->lchild);
		PreOrder(p->rchild);
	}
}//先序遍历

void InOrder(BiTree p) {
	if (p != NULL) {
		InOrder(p->lchild);
		visit(p);
		InOrder(p->rchild);
	}
}//中序遍历

void PostOrder(BiTree p) {
	if (p != NULL) {
		PostOrder(p->lchild);
		PostOrder(p->rchild);
		visit(p);
	}
}//后序遍历
        层次遍历的相关代码操作
void LevelOrder(BiTree T) {
	LinkQueue Q;
	InitQueue(Q);//初始化一个队列Q
	BiTree q;
	EnQueue(Q, T);
	while (!IsEmpty(Q))
	{
		DeQueue(Q, q); 
		visit(q);
		if (q->lchild != NULL)
			EnQueue(Q, q->lchild);
		if (q->rchild != NULL)
			EnQueue(Q, q->rchild);
	}

}

一定要记得队列加&符号，这个错误找了半天红火火恍恍惚！

   运行结果如下图所示：

2.数据结构自命题的代码题练习（树的相关代码题）（自用）

 1.编写后序遍历的非递归代码

具体代码实现：

//后序遍历的非递归算法描述
void PostOrder2(BiTree T) {
	stack *S;//建立一个链栈
	Initstack(S);
	BiTNode* p = T;
	BiTNode* r = NULL;
	while (p||!Empystack(S))
	{
		if (p) {
			Push(S,p);
			p = p->lchild;
		}
		else
		{
			GetTop(S, p);
			if (p->rchild && p->rchild != r)
				p = p->rchild;
			else
			{
				Pop(S,p);
				visit(p->data);
				r = p;//记录最近访问过的站点
				p = NULL;//重置p指针
			}
		}
	}
}

注：这里需要用到链栈的代码可以参照以前学过的先完成链栈的相关操作，在进行后序遍历相关代码的编写。

2.统计二叉树的高度代码实现

递归遍历实现：

int x;//全局变量用来记录返回的函数值
int CountHigh(BiTree T) {
	int lh, rh;
	int depth;
	if (T == NULL) {
		return 0;
	}
	else
	{
		lh = CountHigh(T->lchild);
		rh = CountHigh(T->rchild);
		if (lh>rh)
		{
			x = lh + 1;
			return lh + 1;
		}
		else
		{
			x = rh + 1;
			return rh + 1;
		}
	}
}

运行结果如图所示：

3.判断给定的二叉树是否为完全二叉树

//判断所给的二叉树是否为完全二叉树
bool isok(tree t)
{
    squeue s;
    s.f=s.r=s.tag=0;
    bool flag=true,ans=true;
    if(t==NULL) ans=true;
    if(!t->lchild&&!t->rchild) ans=true;
    enters(s,t);
    treenode *p;
    while(!isempty(s))
    {
        outs(s,p);
        if(!p->lchild)
        {
            flag=false;
            if(p->rchild) ans=false;
        }
        else//有左孩子
        {
            if(flag)//之前不存在缺孩子的节点
            {
                enters(s,p->lchild);
                if(p->rchild) enters(s,p->rchild);
                else flag=false;
            }
            else//之前存在缺孩子的节点
                ans=false;
        }
    }
    if(ans) return true;
    return false;
}

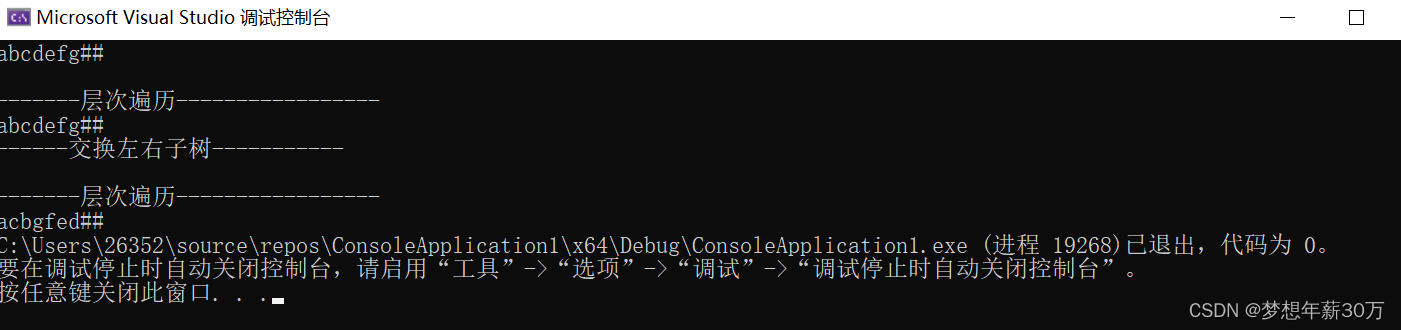
4.交换左右子树

//交换左右子树
void Swap(BiTree &T) {
	BiTNode* temp;
	if (T != NULL) {
		Swap(T->lchild);
		Swap(T->rchild);
		temp = T->lchild;
		T->lchild = T->rchild;
		T->rchild = temp;
	}
}

代码运行结果展示：

5.假设二叉树采用二叉链存储结构存储，设计-个算法，求先序遍历序列中第k(1≤k≤二叉树中结点个数)个结点的值.

代码执行：

int i=1;//全局计数节点
char ch;//记录节点的数据域
char PreOrder_Serch_k(tree t,int k) {
    if (t == NULL) return '#';
    if (t != NULL) {
        if (i == k) {
            return t->data;
        }
        else
        {
            i++;
            ch = PreOrder_Serch_k(t->lchild,k);
            if (ch != '#') return ch;
            ch = PreOrder_Serch_k(t->rchild, k);
            return ch;
        }
    }
}

//测试用例
//        A
//    B       C
//D      E  G    H 

//ABD##E##CG##H##

结果展示：

6.已知二叉树以二叉链表存储，编写算法完成:对于树中每个元素值为x的结点，删去以它为根的子树，并释放相应的空间。

代码编写：

//已知二叉树以二叉链表存储，编写算法完成:对于树中每个元素值为x的结点，删去以它为根的子树，并释放相应的空间。

//删除节点函数设置
void deleteTree(tree &t) {
    if (t == NULL) return;
     deleteTree(t->lchild);
     deleteTree(t->rchild);
     free(t);
}

void  Delete(tree &t, char x) {
     if (t->data == x) {
            deleteTree(t);
            t = NULL;//手动设置根节点为空
        }
       if(t!=NULL)
        {
            Delete(t->lchild, x);
            Delete(t->rchild, x);
        }
}

void preorder(tree t) {
    if (t != NULL) {
        cout << t->data << " ";
        preorder(t->lchild);
        preorder(t->rchild);
    }
}

int main()
{

    tree t;
    buildtree(t);
    Delete(t, 'C');
    preorder(t);
    return 0;
}


//测试用例
//        A
//    B       C
//D      E  G    H 

//ABD##E##CG##H##

7.设一棵二叉树的结点结构为(LLINK, INFO, RLINK)，ROOT为指向该二叉树根结点的指针，p和q分别为指向该二叉树中任意两个结点的指针，试编写算法ANCESTOR(ROOT,P,q,r)，找到P和q的最近公共祖先结点r。

代码编写：

#include "stdio.h"
#include <corecrt_malloc.h>

typedef struct treenode {
    char data;
    struct treenode* lchild, * rchild;
}treenode, * tree;


typedef struct sqstack {
    tree t;
    int tag;//标记访问过的节点
}sqstack;


//先序建树
void buildtree(tree& t)
{
    char ch;
    ch = getchar();
    if (ch == '#') t = NULL;
    else
    {
        t = (treenode*)malloc(sizeof(treenode));
        t->data = ch;
        t->lchild = NULL;
        t->rchild = NULL;
        buildtree(t->lchild);
        buildtree(t->rchild);
    }
}


tree Ancestor(tree t, treenode* p, treenode* q) {
    int top1 = 0;//指向栈的栈顶
    int top2;
    sqstack s1[10],s2[10];//生成两个顺序栈
    treenode* root = t;
    while (root!=NULL||top1>0)
    {
        //将左孩子压入栈中
        while (root!=NULL)
        {
            s1[++top1].t = root;//依次入栈
            s1[top1].tag = 0;//左孩子访问过进行标记
            root = root->lchild;//继续向左进行遍历
        }
        while (top1!=0&&s1[top1].tag==1)//当栈不为空且右孩子存在时将右孩子压入栈中
        {
            //如果栈顶的结点就是p 就复制到栈2中 栈2的栈顶指针此时赋值 top1
            if (s1[top1].t == p)
            {
                for (int i = 1; i <= top1; i++)
                {
                    s2[i] = s1[i];
                }
                top2 = top1;
            }
            //如果栈顶的结点就是q 与栈一进行匹配  
            if (s1[top1].t == q)
            {
                for (int i = top1; i > 0; i--)
                {
                    for (int j = top2; j > 0; j--)
                    {
                        if (s2[j].t == s1[i].t)
                            return s1[i].t;
                    }
                }
            }
            top1--;   //退栈
        }
       //如果栈不空且存在右孩子节点，转向遍历右右子树
        if (top1 != 0) {
            s1[top1].tag = 1;
            root = s1[top1].t->rchild;
        }
    }
    return NULL;
}

int main()
{

    tree t;    
    buildtree(t);
    treenode* p = t->rchild->lchild, * q = t->rchild->rchild;
    printf("%c", Ancestor(t, p, q)->data);
    return 0;
}


//测试用例
//        A
//    B       C
//D      E  G    H 

//ABD##E##CG##H##

测试结果：

8.假设二叉树采用二叉链表存储结构，设计一个算法，求非空二叉树b的宽度(即具有结点数最多的那一层的结点个数)。

代码编写：

#include "stdio.h"
#include <corecrt_malloc.h>

typedef struct treenode {
    char data;
    struct treenode* lchild, * rchild;
}treenode, * tree;

typedef struct {
    tree data[20];//记录树中的数据域
    int level[20];//记录树节点的层次
    int front, rear;//队列头和队列尾
}Queue;

//先序建树
void buildtree(tree& t)
{
    char ch;
    ch = getchar();
    if (ch == '#') t = NULL;
    else
    {
        t = (treenode*)malloc(sizeof(treenode));
        t->data = ch;
        t->lchild = NULL;
        t->rchild = NULL;
        buildtree(t->lchild);
        buildtree(t->rchild);
    }
}
int CountWith(tree t) {
    Queue q;//创建一个顺序队列
    q.front = q.rear = -1;//初始化队列为空
    q.rear++;//记录根节点
    q.data[q.rear] = t;//根节点入队
    q.level[q.rear] = 1;//根节点所在的层次
    treenode* n;
    int m;//保存出队节点的层数
    while (q.front < q.rear)//队列不为空时的循环条件
    {
        q.front++;//后移队头指针
        n = q.data[q.front];
        m = q.level[q.front];//头节点的层数
        if (n->lchild != NULL) {//根节点的左孩子不为空入队
            q.rear++;
            q.data[q.rear] = n->lchild;//左孩子入队
            q.level[q.rear] = m + 1;
        }
        if (n->rchild != NULL) {
            q.rear++;
            q.data[q.rear] = n->rchild;//有孩子入队
            q.level[q.rear] = m + 1;
        }
    }

    int max = 0;//记录最大宽度
    int i = 0;//遍历数组
    int num;//记录每层的节点数
    m = 1;//从第一层开始
    while (i <= q.rear)
    {
        num = 0;
        while (i <=q.rear && q.level[i] == m)
        {
            num++;
            i++;
        }
        m = q.level[i];
        if (num > max) {
            max = num;
        }
    }
    printf("\n此二叉树最大的宽度为:%d", max);
    return max;
}


int main()
{

    tree t;
    buildtree(t);
    CountWith(t);
    return 0;
}


//测试用例
//        A
//    B       C
//D      E  G    H 

//ABD##E##CG##H##

运行结果：

9.设有一棵满二叉树(所有结点值均不同)，已知其先序序列为pre,设计一个算法求其后序序列post.

运行代码：

10.设计一个算法将二叉树的叶结点按从左到右的顺序连成-一个单链表，表头指针为head.二叉树按二叉链表方式存储，链接时用叶结点的右指针域来存放单链表指针。

#include "stdio.h"
#include <corecrt_malloc.h>

typedef struct treenode {
    char data;
    struct treenode* lchild, * rchild;
}treenode, * tree;

//先序建树
void buildtree(tree& t)
{
    char ch;
    ch = getchar();
    if (ch == '#') t = NULL;
    else
    {
        t = (treenode*)malloc(sizeof(treenode));
        t->data = ch;
        t->lchild = NULL;
        t->rchild = NULL;
        buildtree(t->lchild);
        buildtree(t->rchild);
    }
}

//单链表的头节点指针
tree head = (treenode*)malloc(sizeof(treenode));
tree pre=NULL ;

tree Inorder(tree t) {
    if (t != NULL) {
        Inorder(t->lchild);
        if (t->lchild == NULL && t->rchild == NULL) {
            if (pre == NULL) {
                head = t;
                pre = t;
            }
            else
            {
                pre->rchild = t;
                pre = t;
            }
        }
        Inorder(t->rchild);
        //递归完成后将pre节点的右指针域置为空
        pre->rchild = NULL;
    }
    return head;
}

int main()
{
    tree p;//遍历单链表的节点
    tree t;
    buildtree(t);
    Inorder(t);
    while (head)
    {
        printf("%c", head->data);
        head = head->rchild;
    }
    return 0;
}


//测试用例
//        A
//    B       C
//D      E  G    H 

//ABD##E##CG##H##

运行结果：

11.试设计判断两科二叉树是否相似的算法。所谓二叉树T1和T2相似，指的是T1和T2都是空的二叉树或都只有一个根结点；或T1的左子树和T2的左子树是相似的，且T1的右子树和T2的右子树是相似的

具体代码：
 

typedef struct treenode {
    char data;
    struct treenode* lchild, * rchild;
}treenode, * tree;

//先序建树
void buildtree(tree& t)
{
    char ch;
    cin >> ch;
    if (ch == '#') t = NULL;
    else
    {
        //分配内存
        t = (treenode*)malloc(sizeof(treenode));
        //赋值
        t->data = ch;
        //左右孩子置空
        t->lchild = NULL;
        t->rchild = NULL;
        //递归的去赋值左右子树
        buildtree(t->lchild);
        buildtree(t->rchild);
    }
}

//相似算法
bool similar(tree t1, tree t2) {
    int left, right;
    if (t1 == NULL && t2 == NULL) return 1;
    else if (t1 == NULL || t2 == NULL) return 0;
    else
    {
        left = similar(t1->lchild, t2->lchild);
        right = similar(t1->rchild, t2->rchild);
        return (left && right);
    }
}


int main()
{
    tree t1;
    tree t2;
    buildtree(t1);
    buildtree(t2);
    printf("%d",similar(t1, t2));
}

运行结果：

12.编程求以孩子兄弟表示法存储的森林的叶子结点数。

具体代码：

#include<stdio.h>
#include <corecrt_malloc.h>
#include <iostream>
using namespace std;

//孩子兄弟表示法
typedef struct treenode {

	struct treenode* children;
	struct treenode* brother;
	int data;
}treenode,*tree;

//建树
void buildtree(tree& t)
{
    char ch;
    cin >> ch;
    if (ch == '#') t = NULL;
    else
    {
        //分配内存
        t = (treenode*)malloc(sizeof(treenode));
        //赋值
        t->data = ch;
        //初始化
        t->children = NULL;
        t->brother = NULL;
        //递归赋值
        buildtree(t->children);
        buildtree(t->brother);
    }
}

int leaves(tree t) {
    //空节点
    if (t == NULL) return 0;
    //没有孩子节点
    if (t->children == NULL) return 1 + leaves(t->brother);
    //有孩子节点
    else
    {
        return leaves(t->children) + leaves(t->brother);
    }
}

int main() {
    tree t;
    buildtree(t);
    printf("%d", leaves(t));
    return 0;
}

/*

         A
     B        F
  D     C   G
   \
    E
ABD#E##C##FG###

*/

运行结果：

13.以孩子兄弟链表为存储结构，请设计递归算法求树的深度。

具体代码：

#include<stdio.h>
#include <corecrt_malloc.h>
#include <iostream>
using namespace std;

//孩子兄弟表示法
typedef struct treenode {

	struct treenode* children;
	struct treenode* brother;
	int data;
}treenode,*tree;

//建树
void buildtree(tree& t)
{
    char ch;
    cin >> ch;
    if (ch == '#') t = NULL;
    else
    {
        //分配内存
        t = (treenode*)malloc(sizeof(treenode));
        //赋值
        t->data = ch;
        //初始化
        t->children = NULL;
        t->brother = NULL;
        //递归赋值
        buildtree(t->children);
        buildtree(t->brother);
    }
}

int CountHigh(tree t) {
    //树空
    if (t == NULL) return 0;
    else
    {
        //递归计算左孩子子树高度
        int l = CountHigh(t->children);
        //递归计算右兄弟子树高度
        int r = CountHigh(t->brother);
        //l+1是因为孩子节点需要向下一层相加
        return max(l + 1, r);
    }

}

int main() {
    tree t;
    buildtree(t);
    printf("%d", CountHigh(t));
    return 0;
}

/*

         A
     B        F
  D     C   G
   \
    E
ABD#E##C##FG###

*/

运行结果：

评论 1
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值