机器学习之贝叶斯分类算法(nlp)

一、贝叶斯公式

条件概率

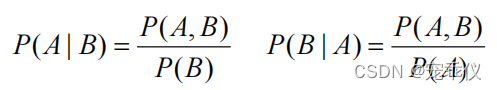
由上式进一步推导

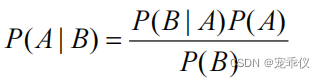
由此，推广到随机变量的范畴，设 X，Y 为两个随机变量，得到贝叶斯公式：

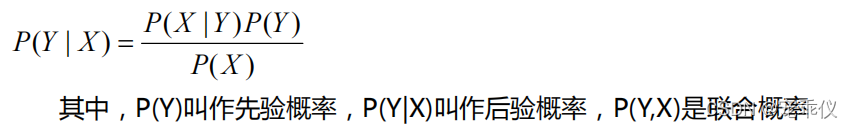
X可以当作实际输入的数据 ，Y是所需要预测的类别

二、朴素贝叶斯算法的优缺点

1、朴素贝叶斯优点：

算法逻辑简单,易于实现（算法思路很简单，只要使用贝叶斯公式转化即可！）

分类过程中时空开销小（假设特征相互独立，只会涉及到二维存储）

2、朴素贝叶斯缺点：

理论上，朴素贝叶斯模型与其他分类方法相比具有最小的误差率。但是实际上并非总是

如此，这是因为朴素贝叶斯模型假设属性之间相互独立，这个假设在实际应用中往往是不成

立的，在属性个数比较多或者属性之间相关性较大时，分类效果不好。

朴素贝叶斯模型(Naive Bayesian Model)的朴素(Naive)的含义是"很简单很天真"地假

设样本特征彼此独立. 这个假设现实中基本上不存在(PCA), 但特征相关性很小的实际情况还是很

多的, 所以这个模型仍然能够工作得很好

 三、朴素贝叶斯算法流程

朴素贝叶斯假设特征之间相互独立

X可以当作实际输入的数据 ，Y是所需要预测的类别

1. 训练数据生成训练样本集：TF-IDF    词频 逆文档频率
2. 对每个类别计算 P(yi)
3. 对每个特征属性计算所有划分的条件概率
4. 对每个类别计算 p(x|yi)p(yi) yi类别aj出现的频率

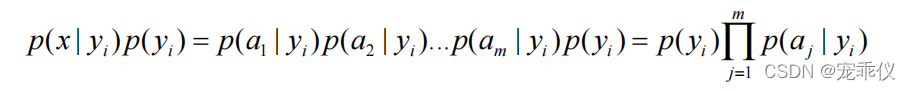
5. 以 p(x|yi)p(yi)的最大项作为 x 的所属类别
   统计语言模型与 NLP 算法设计_宠乖仪的博客-优快云博客
6. HMM算法_宠乖仪的博客-优快云博客