深度学习查漏补缺：4.数据分布的度量

一、数据分布差异的度量

1.KL散度（Kullback-Leibler Divergence）

        什么是KL散度？
        KL散度是一种用来衡量两个概率分布之间差异的工具。你可以把它想象成一个“距离测量器”，但它不是传统意义上的距离（比如两点之间的直线距离），而是更像在比较两个分布的“相似程度”。简单来说，它告诉你：一个分布（P）有多像另一个分布（Q），或者说要把P“伪装”成Q需要付出多大的代价。

        关键词：概率分布、差异、不对称。
        本质：KL散度不是对称的，也就是说，P到Q的“距离”和Q到P的“距离”通常不一样。

        用一个生活中的比喻:
        假设你有两个朋友，一个喜欢吃甜食（P分布），另一个喜欢吃辣食（Q分布）。你想让甜食朋友假装成辣食朋友，去骗过一群美食家：
        如果甜食朋友（P）只知道甜品的味道，要模仿辣食朋友（Q）的口味，他需要学习辣椒的味道、麻的口感等等，这个“学习成本”就是KL散度（从P到Q）。
        反过来，如果辣食朋友（Q）要假装成甜食朋友（P），他需要学甜品的甜度和奶油味，这个“学习成本”是另一个KL散度（从Q到P）。
        因为甜食和辣食的差异方向不同，这两个“伪装成本”通常不一样。

        KL散度的值越小，说明两个分布越相似；值越大，说明差异越大。

        KL散度的特点:
        1. 非负性：KL散度总是大于等于0。如果等于0，说明两个分布完全一样（P = Q）。
        2. 不对称性：从P到Q的KL散度和从Q到P的KL散度通常不同。就像甜食朋友学辣食和辣食朋友学甜食的难度不一样。
        3. 信息论背景：它来自信息论，可以理解为“用Q来编码P的信息时多花了多少力气”。

        一个简单的例子
        假设你有两袋糖果：
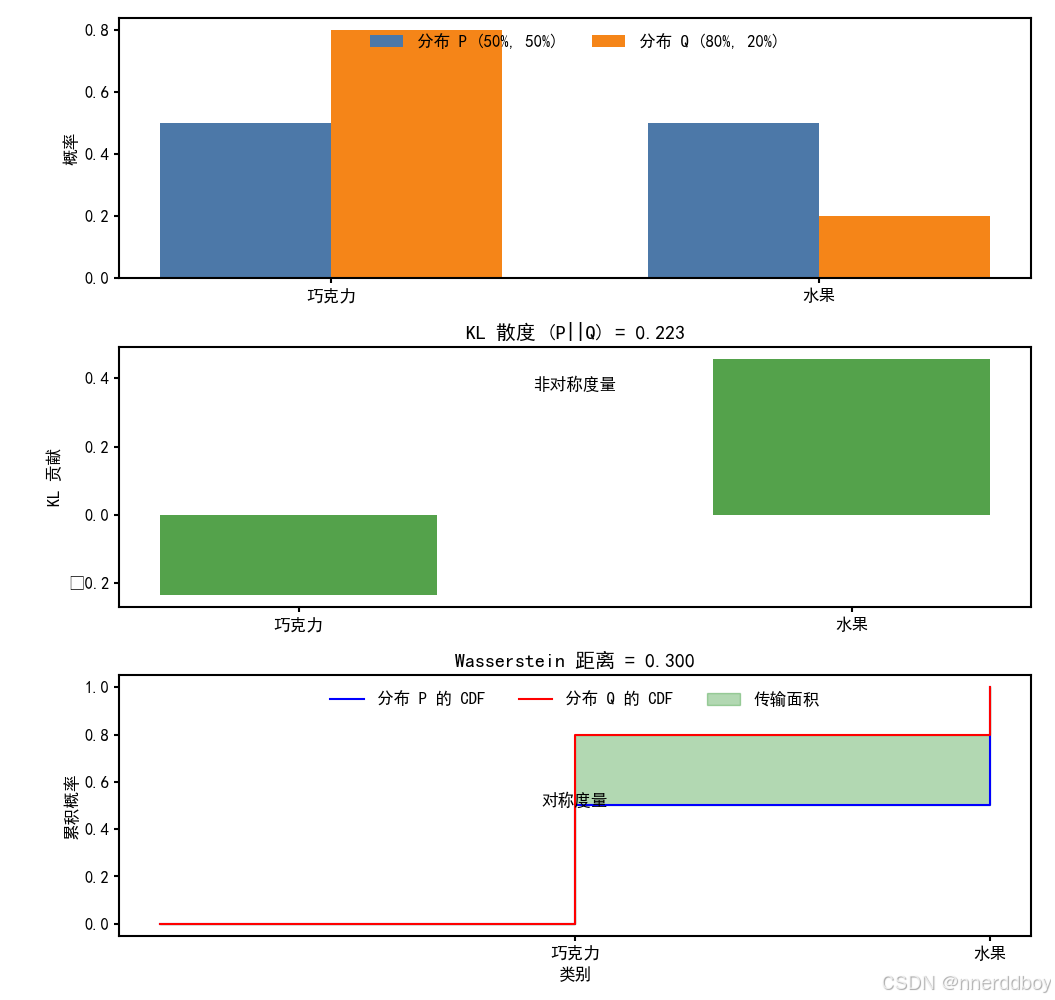
        袋子P：50%巧克力糖，50%水果糖。
        袋子Q：80%巧克力糖，20%水果糖。

        现在你想用袋子Q的分布（80%巧克力，20%水果）去描述袋子P（50%巧克力，50%水果）：
        在P的世界里，水果糖和巧克力糖一样常见，但Q认为水果糖很少。如果你用Q的“眼光”去看P，就会低估水果糖的出现频率。
        KL散度（P到Q）会告诉你：用Q来模拟P有多不靠谱，需要额外调整多少。

        反过来，用P去模拟Q（从Q到P），则是另一种调整，因为P会高估水果糖的概率。两种方向的调整成本不同，所以KL散度不对称。

        计算KL散度的大致思路：
1. 看P和Q在每个点上的概率。
2. 对每个点，算P的概率除以Q的概率，取对数，再乘以P的概率。
3. 把所有点的结果加起来，就得到了KL散度。

        用糖果例子来说，就是比较每个糖果类型（巧克力、水果）的比例差异，再综合起来看总的“伪装难度”。

        总结
        KL散度是个衡量分布差异的工具，像是在问“一个分布假装成另一个分布有多难”。
        它不对称，值越小越相似，等于0时完全一样。
        在你的迁移学习任务中，可以用它挑出跟目标域最像的源域数据，或者优化模型让源域和目标域“看起来更像”。

2.Wasserstein距离

什么是Wasserstein距离？

        Wasserstein距离是用来衡量两个概率分布之间差异**的一种方法。你可以把它想象成一个“搬运工”，它的任务是把一个分布的“货物”（概率质量）搬到另一个分布的位置上，而Wasserstein距离就是完成这个搬运工作所需要的最小“总成本”。

        关键词：概率分布、搬运、最优成本。
        本质：它考虑了分布之间的“几何形状”和“位置关系”，比KL散度更直观地反映分布的实际距离。

        用一个生活中的比喻
        想象你有两个堆沙子：
        堆P：一堆沙子在操场左边。
        堆Q：另一堆沙子在操场右边，距离左边10米。

        你的任务是用铲子把P的沙子搬到Q的位置，变成Q的形状：
        如果P和Q的沙子总量一样（都是1吨），你需要把1吨沙子从左边搬到右边10米。
        搬运的“成本”就是：沙子重量（1吨） × 搬运距离（10米） = 10吨·米。
        这个“最小搬运成本”就是Wasserstein距离。

        如果P和Q的形状不同（比如P是尖尖的沙堆，Q是扁平的沙堆），你还需要调整沙子的分布形状，成本会更复杂，但核心还是“搬运距离 × 搬运量”的总和。

       Wasserstein距离的特点:
        1. 对称性：不像KL散度，Wasserstein距离是对称的，从P到Q和从Q到P的距离是一样的（搬沙子从左到右和从右到左成本相同）。
        2. 几何意义：它考虑了分布之间的“空间距离”，更像现实中的直观距离。
        3. 非负性：距离总是大于等于0，如果两个分布完全一样，距离为0。
        4. 搬运计划：它会找到最优的搬运方式，让总成本最小。

        一个简单的例子
        假设有两个商店的苹果库存分布：
        商店P：50%苹果在仓库A，50%在仓库B。
        商店Q：80%苹果在仓库A，20%在仓库B。
        仓库A和仓库B相距10公里。

        你需要把P的苹果分布调整成Q的分布：
        P有50%的苹果在B（0.5个单位），Q只有20%在B（0.2个单位），所以要从B搬0.3个单位的苹果到A。
        搬运成本 = 0.3 × 10公里 = 3公里。
        这里假设总苹果量是1个单位，Wasserstein距离就是3。

        这个距离告诉你：要把P变成Q，最少需要搬运3公里·单位的苹果。反过来从Q到P也是一样的成本。

        和KL散度的区别：还记得前面讲的KL散度吗？KL散度像是在比较两个分布的“信息伪装难度”，它不关心分布的空间位置，只看概率值本身。而Wasserstein距离更像“物理搬运”，它会考虑分布的“位置”和“形状”：
        如果两个分布概率值完全一样（比如P和Q都是50% A，50% B），KL散度是0，Wasserstein距离也是0。
        但如果P和Q位置不同（比如P在左边，Q在右边10米），KL散度只看概率值可能觉得差不多，但Wasserstein距离会算上这10米的搬运成本。

        计算Wasserstein距离的大致思路：
        1. 把两个分布想象成两堆沙子。
        2. 找到一种最优的搬运方案：从P的每个点搬多少沙子到Q的每个点。
        3. 计算每条搬运路线的成本（距离 × 搬运量），然后加起来取最小值。

        在实际中，计算机用优化算法（比如线性规划）来算这个最小成本。

        Wasserstein距离就像一个搬运工，计算把一个分布“搬”成另一个分布的最小成本。
        它对称、有几何意义，适合比较分布的位置和形状差异。

Python代码示例：

import numpy as np
import matplotlib.pyplot as plt
from scipy.stats import wasserstein_distance

P = np.array([0.5, 0.5])
Q = np.array([0.8, 0.2])
categories = ['巧克力', '水果']

eps = 1e-10
P = P + eps; P = P / P.sum()
Q = Q + eps; Q = Q / Q.sum()

kl_div = np.sum(P * np.log(P / Q))

values = np.array([0, 1])
wasserstein_dist = wasserstein_distance(values, values, P, Q)

cdf_P = np.cumsum(P)
cdf_Q = np.cumsum(Q)

plt.rcParams.update({
    'font.family': 'SimHei',  
    'font.size': 12,
    'axes.linewidth': 1.5,
    'lines.linewidth': 1.5,
    'xtick.major.width': 1.5,
    'ytick.major.width': 1.5,
})

fig, (ax1, ax2, ax3) = plt.subplots(3, 1, figsize=(8, 10), sharex=False)

# 子图 1：原始分布
x = np.arange(len(categories))
width = 0.35
ax1.bar(x - width/2, P, width, label='分布 P (50%, 50%)', color='#4C78A8')
ax1.bar(x + width/2, Q, width, label='分布 Q (80%, 20%)', color='#F58518')
ax1.set_xticks(x)
ax1.set_xticklabels(categories)
ax1.set_ylabel('概率')
ax1.legend(frameon=False, loc='upper center', ncol=2)

# 子图 2：KL 散度的贡献
kl_contribution = P * np.log(P / Q)
ax2.bar(x, kl_contribution, width=0.5, color='#54A24B')
ax2.set_xticks(x)
ax2.set_xticklabels(categories)
ax2.set_ylabel('KL 贡献')
ax2.set_title(f'KL 散度 (P||Q) = {kl_div:.3f}')
ax2.text(0.5, max(kl_contribution)*0.8, '非对称度量', ha='center')

# 子图 3：Wasserstein 距离的 CDF 差异
ax3.step([0, 1, 2], [0, *cdf_P], 'b-', label='分布 P 的 CDF', where='post')
ax3.step([0, 1, 2], [0, *cdf_Q], 'r-', label='分布 Q 的 CDF', where='post')
ax3.fill_between([0, 1, 2], [0, *cdf_P], [0, *cdf_Q], step='post', color='green', alpha=0.3, label='传输面积')
ax3.set_xticks([1, 2])
ax3.set_xticklabels(categories)
ax3.set_xlabel('类别')
ax3.set_ylabel('累积概率')
ax3.set_title(f'Wasserstein 距离 = {wasserstein_dist:.3f}')
ax3.text(1, 0.5, '对称度量', ha='center')
ax3.legend(frameon=False, loc='upper center', ncol=3)

plt.tight_layout()
plt.show()