散列表的构建

散列表需要将关键码用散列技术进行存储，才可以进行散列查找，

散列查找是典型的用空间换时间的算法，只要散列函数设计的合理，则散列表越长，冲突的概率越低。

常见散列函数：      

除留余数法，H(key)=key%13;  散列表的表长为m， 取一个不大于 m最接近或者等于m的质数p （质数：指除了1和此整数自身外，不能被其他自然数整除的数，如8可以被2整除，所以8不是质数）p取质数，可以达到让不同关键字的冲突尽可能地少。

 直接定址法： H(key)=key   或 H(key)=a*key + b;   其中a，b都是常数， 这种方法计算最简单，且不会产生冲突，它适合关键字的分布基本连续的情况，若关键字分布不连续，空位比较多(假设有一些同学退学了，则就删除了他们的学生信息，但是数组中那个位置还是存在的，所以会造成浪费)，则会造成浪费。例如: 存储同一个班级的学生信息，班内学生学号为(1120112176~1120112205), 则H(key)=key-1120112176,    这样每一个学生对应一块地址，如图:

 3.数字分析法:  我们的手机号前三位基本只有那么几类，所以每个人的手机号几乎只有后四位不同，则可以选择构建一个0~9999的数组，将每个手机号末尾四位相同的放在对应的数组地址中，这种方法适合于已知的关键字集合，只有某些位的数字分布不均匀，其他数字几乎均匀的情况下，此时选取数字分布均匀的若干为作为散列地址， 如图：

 4.平方取中法:  取关键字的平方值的中间几位作为散列地址，  这种方法得到的散列地址与关键字的每位都有关系，适用于 关键字的每位取值都不够均匀的元素。 如图:

这种封闭数组会有冲突的情况，所以可以使用拉法解决冲突

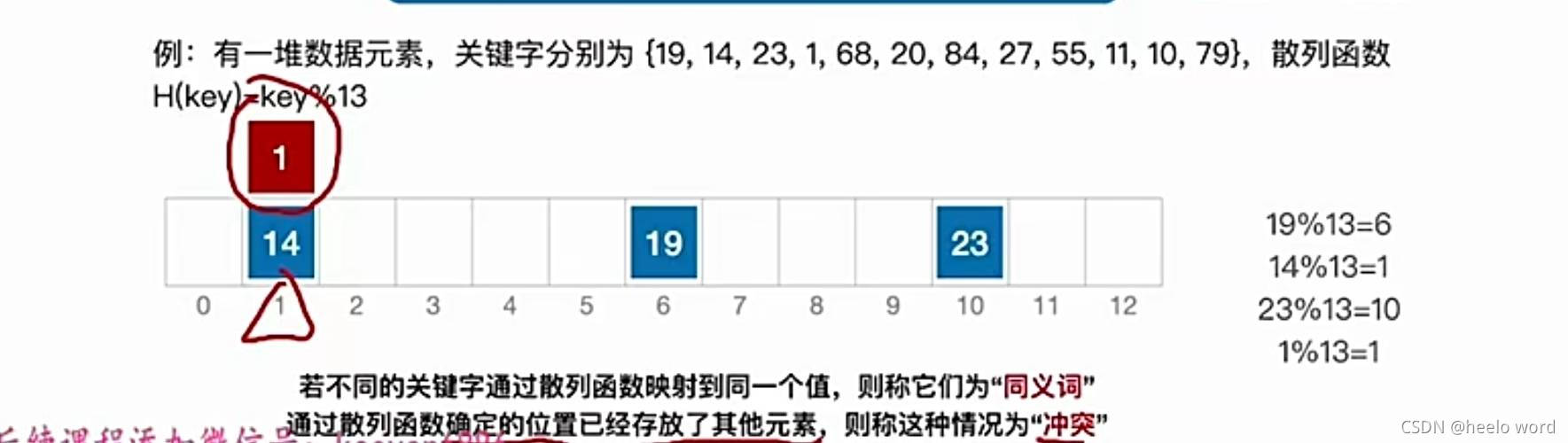
查找长度： 在查找运算中， 需要对比关键字的次数称为查找长度

处理冲突的方法

方法一:   开放定址法

开放定址法就是一旦发生了冲突，就去寻找下一个空的散列地址，只要散列表足够大，空的散列地址总能找到，并将记录存入。

同义词:两个关键字key1 ≠ key2，但是却有f(key1)=f(key2), 这种现象我们称为冲突，并把key1 和key2称为散列函数的同义词。key实际就是要存储的数据， f(key)表示映射到索引的值。、

 

线性探测法：散列表如上图所示，现在有新元素48插入， 48%12=0， 但是此时索引0已经存放元素了， 所以开始往下一个元素移动， 该索引任然有元素，继续往后移动，只要散列表足够的，就总会有空为存放新数据。

位移公式：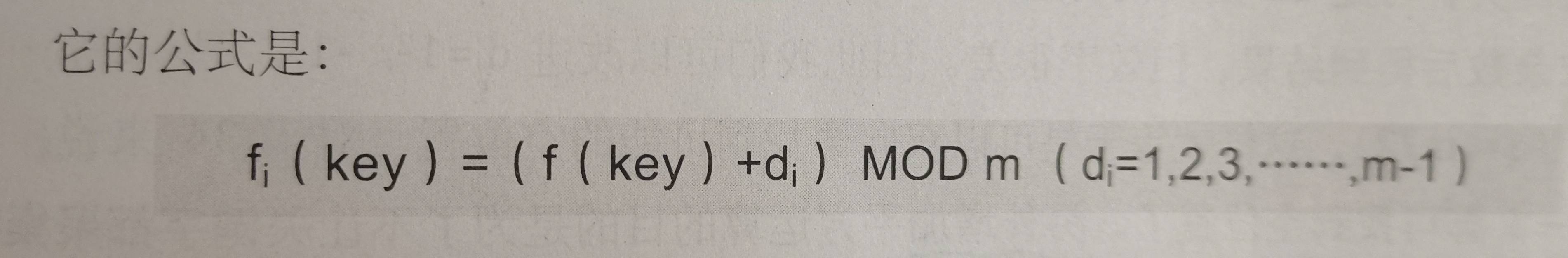

以元素48为例， 首先48%12=0， 但是索引0上有元素，则(48+1)%12=1, 索引为1的位置也有元素，则(48+2)%12=2, 依次类推，直到有空位为止。

方法二 ：  二次探测：此时散列表如图所示。

 当key=34时候， 34%12=10， 但是很明显索引10后面已经没有位置了， 是不可能再存放数据的， 但是索引10的前面有位置，则又有了新的探测方法。

移位公式:

 这种查找等于是一个双向寻找到可能的空位置。  对于34来说，我们取di=-1即可找到空位置了。

方法三 ：  拉链法(链地址法)

用拉链法可以有效处理冲突，数组只保存一个指向某个数据元素的指针，所有的数据元素都保存在这个指针域中，用尾插法将元素连接在链表的尾部(连接在头部也可以)

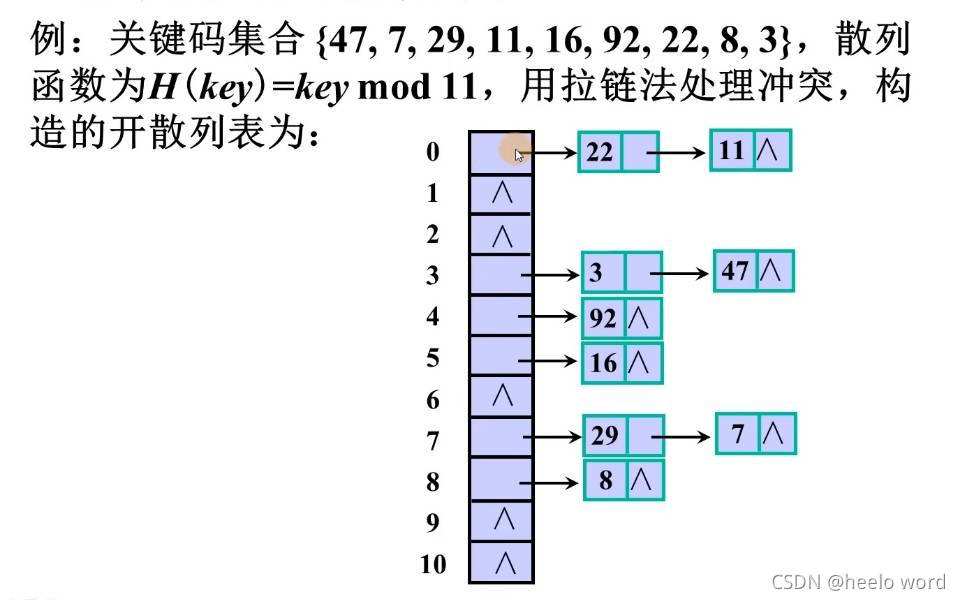
查找目标：  例如查找27元素，  若数组中是对13取余

查找27， 27%13=1；  所以如果27这个元素存在的话，就一定在数组索引为1的链表里面