【笔记】数据结构与算法 python-04-排序

列表排序

将一组无序的记录序列调整为有序的记录序列（升序与降序，Python内置函数sort()）

输入：列表

输出：有序列表

常见的排序方法

初级排序方法	高级排序方法	其他排序方法
冒泡排序	快速排序	希尔排序
选择排序	堆排序	计数排序
插入排序	归并排序	计数排序、桶排序

初级排序

冒泡排序

依次比较相邻元素，若顺序（大小排列方式）不对则交换位置，否则仅向后推移指针。从表头到表尾重复进行（一次只会将当前无序区最大的数放到尾，重复n-1次，列表将从小到大正确排序），直到对所有元素都按照正确的排序结束。时间复杂度为O()。不适用于大规模数据集。

无序区（不是正确排序）从头到尾运行一次，会导致无序区减少一个数，有序区会增加一个数。

动态演示如下： 

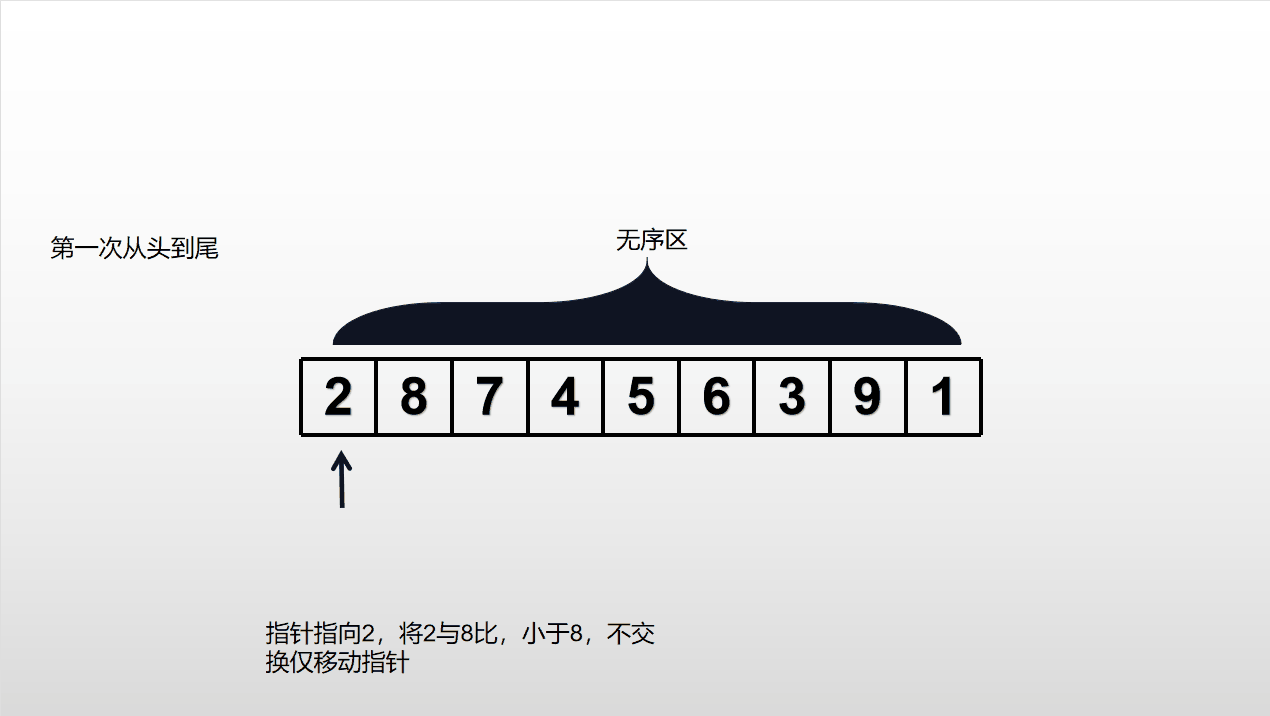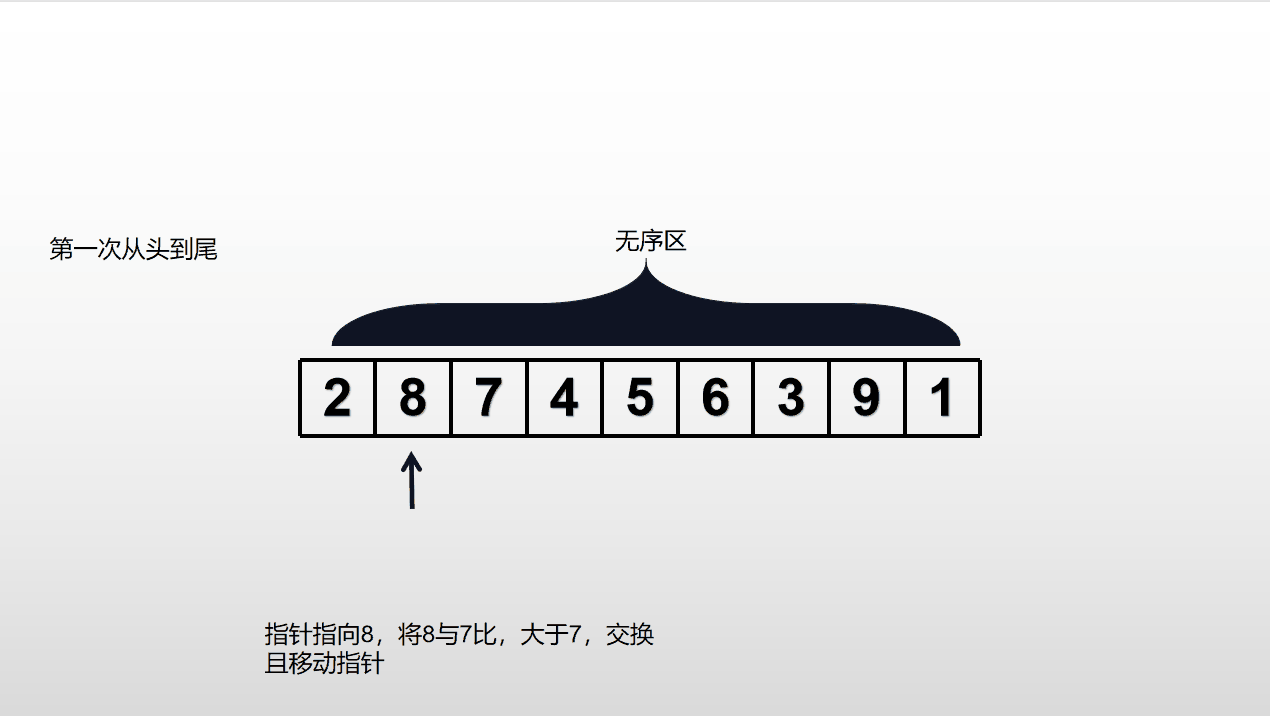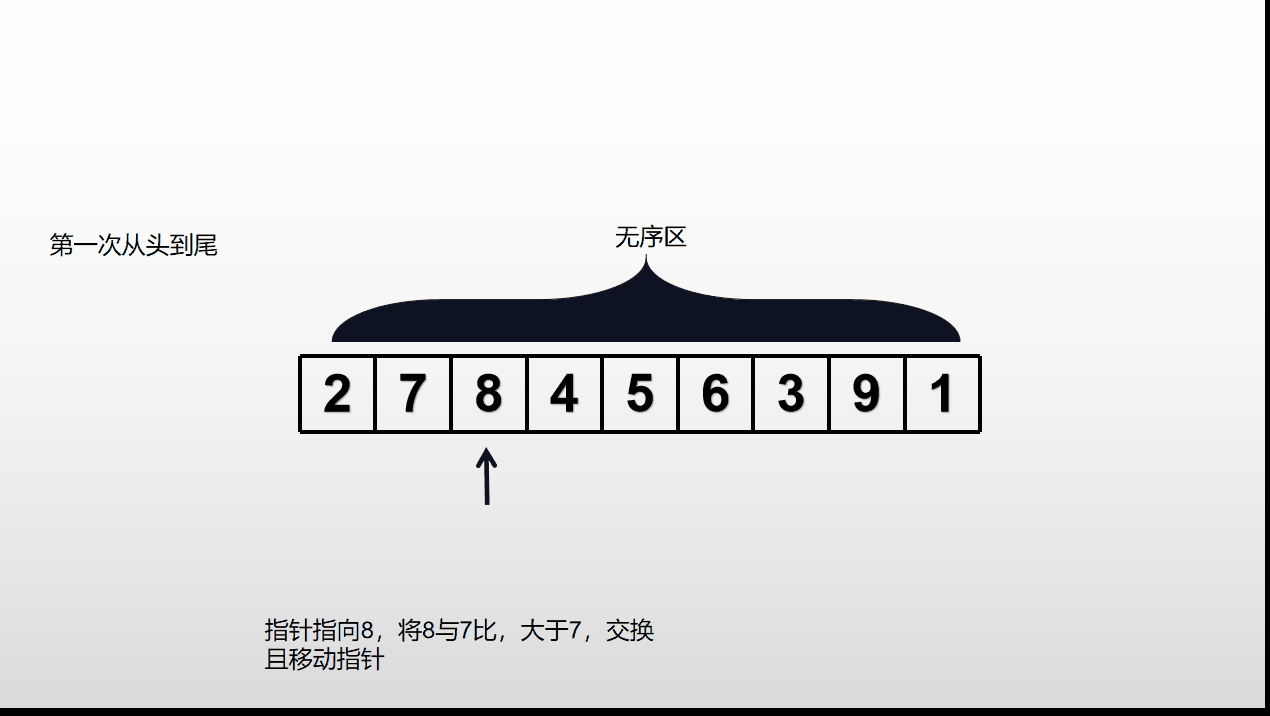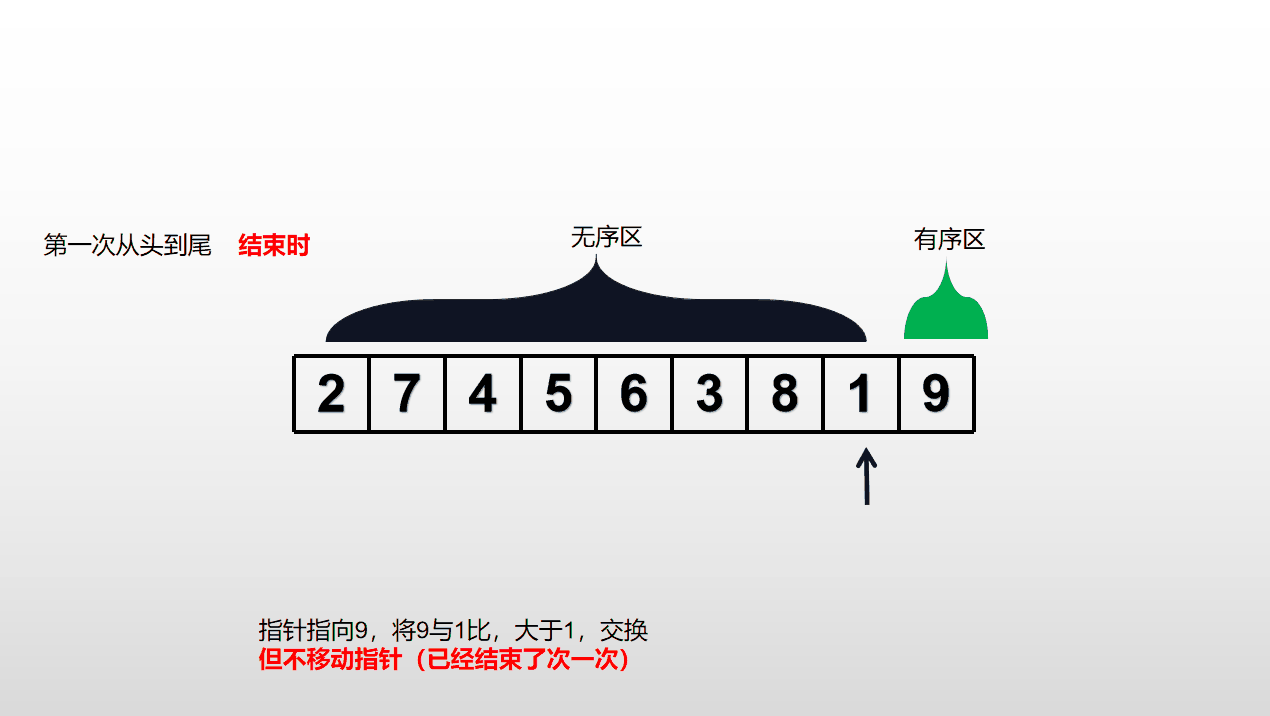对应代码如下：

def bubble_sort(ls):
    for i in range(len(ls) - 1 ):        #最多需要进行n-1次从头到尾运算（最后一次两个最小的数以及经完成排序）
        for j in range(len(ls)-i-1):    #每经历一次，无序区的长度会减1
            #比较相邻元素，可升序也可降序
            if ls[j] > ls[j+1]:      #升序
                ls[j], ls[j+1] = ls[j+1], ls[j]
    return ls

arr = [64, 34, 25, 12, 22, 11, 90]
sorted_arr = bubble_sort(arr)
print(sorted_arr)                     # 输出 [11, 12, 22, 25, 34, 64, 90]
        

 我们应该要想到，如果其中某些子集块已经是排序状态，我们就不需要进行额外的计算了，举一个极端的例子，当输入的整个序列是有序状态，那么应该直接返回，无需进行排序。所以我们应该加入一个标志符：

def bubble_sort(ls):
    for i in range(len(ls) - 1):        #最多需要进行n-1次从头到尾运算（最后一次两个最小的数以及经完成排序）
        swapped = False                 #判断是否发生了交换
        for j in range(len(ls)-i-1):    #每经历一次，无序区的长度会减1
            #比较相邻元素，可升序也可降序
            if ls[j] > ls[j+1]:      #升序
                ls[j], ls[j+1] = ls[j+1], ls[j]
                swapped = Ture
        #当一次不需要交换时，往后的排序中也不会发生交换，此时即可返回
        if not swapped:
            return ls
    return ls

arr = [1, 2, 3, 4, 5, 6, 9]
sorted_arr = bubble_sort(arr)
print(sorted_arr)                     # 输出 [1, 2, 3, 4, 5, 6, 9]

选择排序

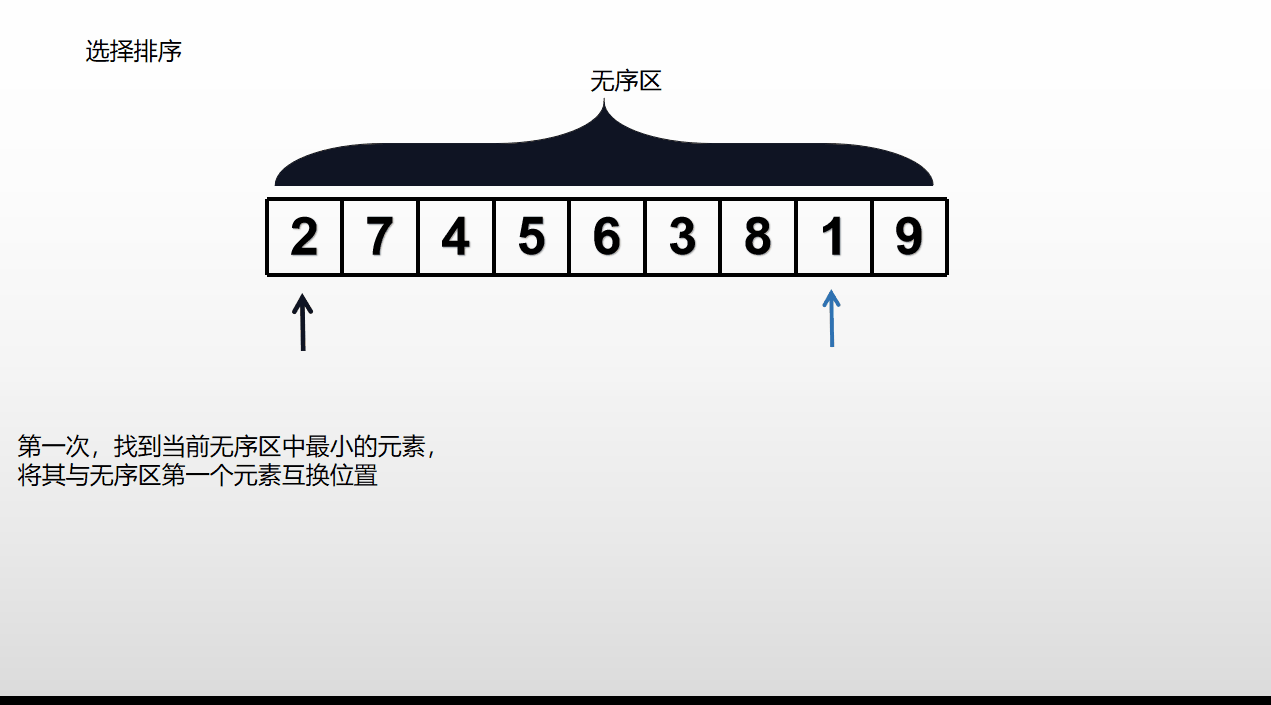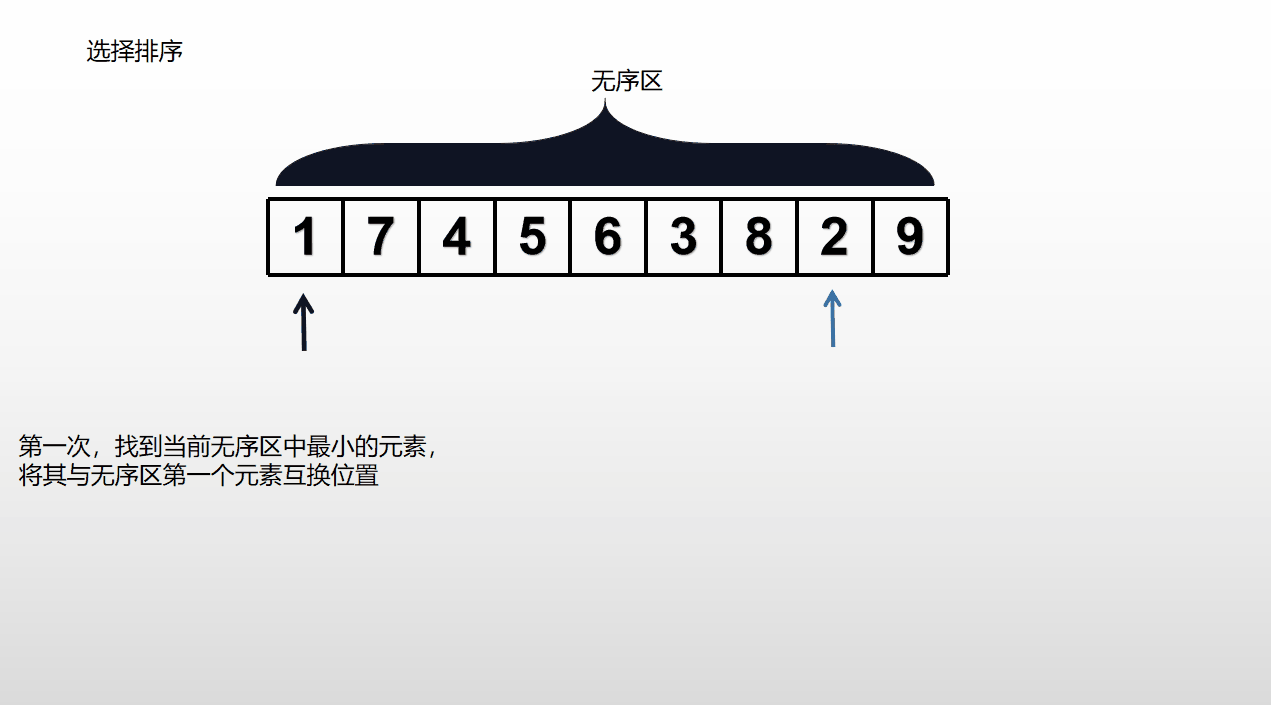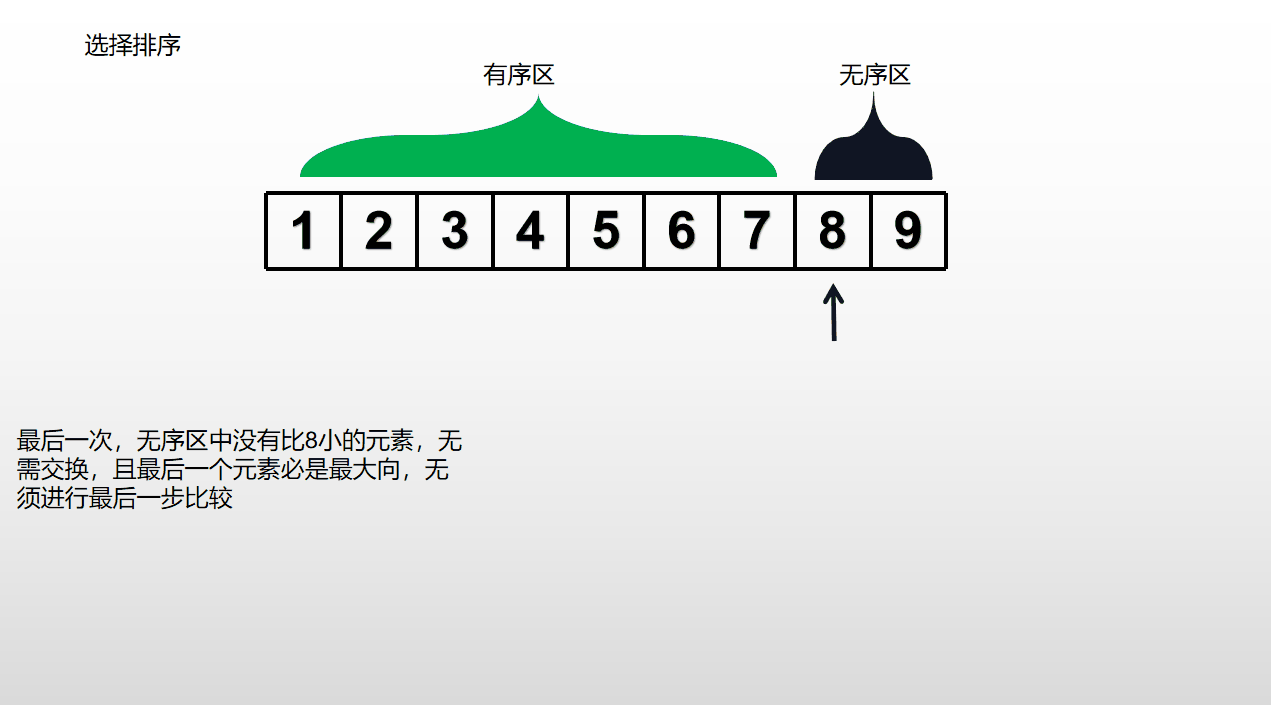
从列表无序区的第一个元素开始，依次找到之后最小的元素，与当前无序区的第一个数据交换位置，重复进行直至完成排序，复杂度也为O()。性能比冒泡排序好一些（因为冒泡排序成功比较一次需要交换一次，而选择排序仅需交换一次），同样不适用于大规模数据。

动态演示如下：

代码如下：

def select_sort(ls):
    for i in range(len(ls) - 1):          #共需n-1次挑选，最后一位无须比较
        min_index = i                   #假设当前无序区为最小值，取其索引，方便交换时使用
        for j in range(i + 1, len(ls)): #已经取过无序区的第一个值，无需重复
            if ls[j] < ls[min_index]:   #当前元素小于第一个元素时，记下其索引，方便交换时使用
                min_index = j           #记录最小值索引
        ls[i], ls[min_index] = ls[min_index], ls[i]    #交换当前无序区最小值与第一个元素位置
    return ls

arr = [64, 34, 25, 12, 22, 11, 90]
sorted_arr = select_sort(arr)
print(sorted_arr)  # 输出 [11, 12, 22, 25, 34, 64, 90]

插入排序

将输入列表分为有序区和无序区两部分，每次取出无序区的第一个元素，将其插入到有序区的正确排序位置，直到所有元素插入完成。复杂度也是O()

图形演示如下：

 代码如下：

def inserct_sort(ls):
    for i in range(1,len(ls)):        #第一个元素无须比较，直接可作为有序区
        temp = ls[i]                  #因为会修改当前索引的值，需要提前保存
        j = i - 1                     #有序区中最后一个元素的下标
        #while循环中，j会一直向左移，但移到最左侧时，应当截止
        #且有序部分的元素大于当前插入元素时，应向后移一位，为当前元素腾出存储空间
#########while循环的作用是找到当前元素的合适位置（比左侧大，比右侧小）        
        while j >= 0 and ls[j] > temp:
            ls[j+1] = ls[j]           #有序区中元素大于当前元素，故向后移一位
            j -= 1                    #接着向有序区左侧移动
        ls[j+1] = temp                #while循环结束，标志着找到当前元素合适的位置，此时，j指的是小于当前元素的值，而j+1处的值由于大于当前元素已经右移至j+2处，所以应将当前元素放在j+1处
    return ls                         #其实可以不加，因为是在ls上进行操作



arr = [12, 11, 13, 5, 6]
print("排序前的数组:", arr)
insertion_sort(arr)
print("排序后的数组:", arr)

########################
排序前的数组: [12, 11, 13, 5, 6]
排序后的数组: [5, 6, 11, 12, 13]

高级排序 

快速排序

选择输入列表中的一个元素作为基准（通常选取第一个元素），将列表中小于等于基准的元素放在其左边，大于基准的元素放在其右边，基准元素放在中间。接着对左右子列表重复操作，直到每个子数组只包含一个元素或者为空停止。

动态演示：

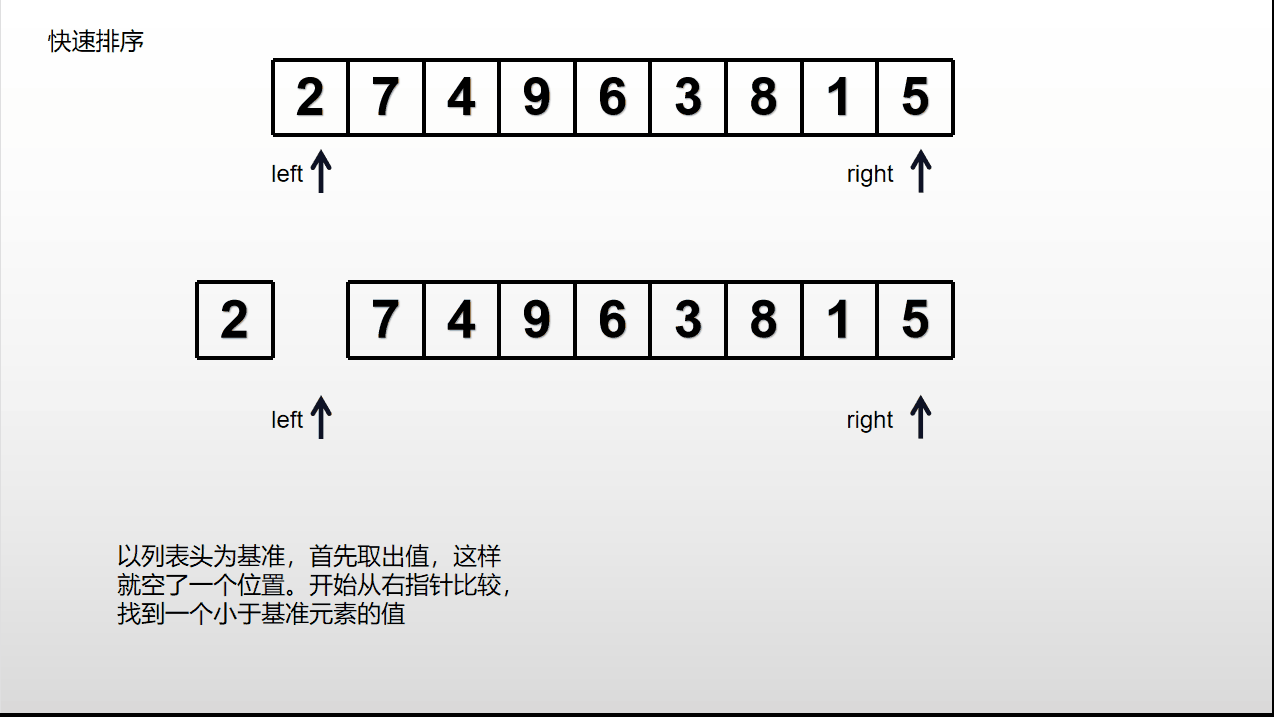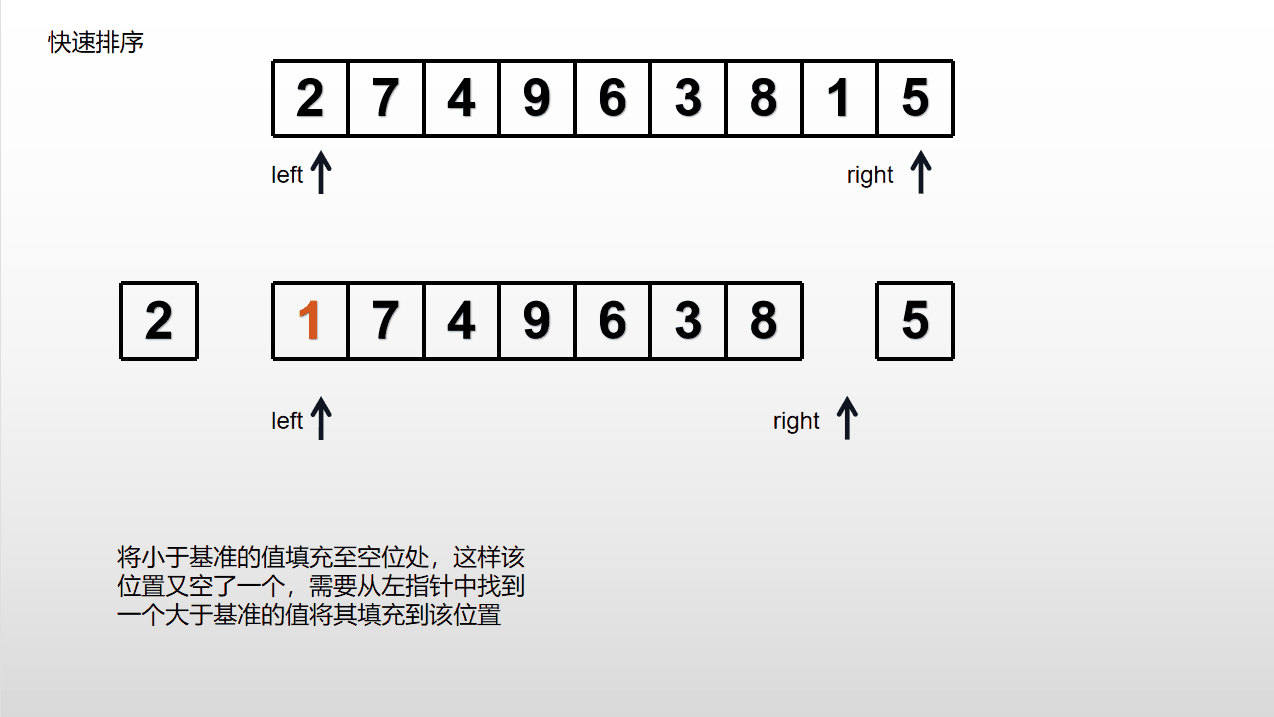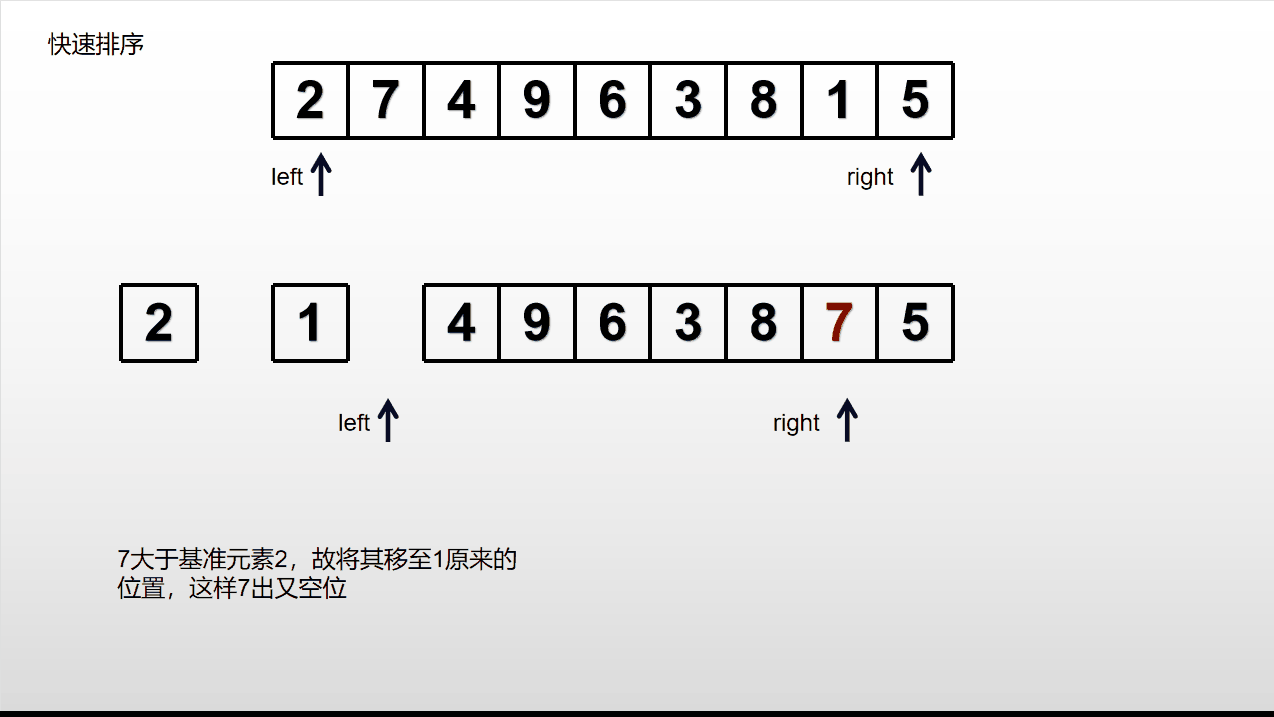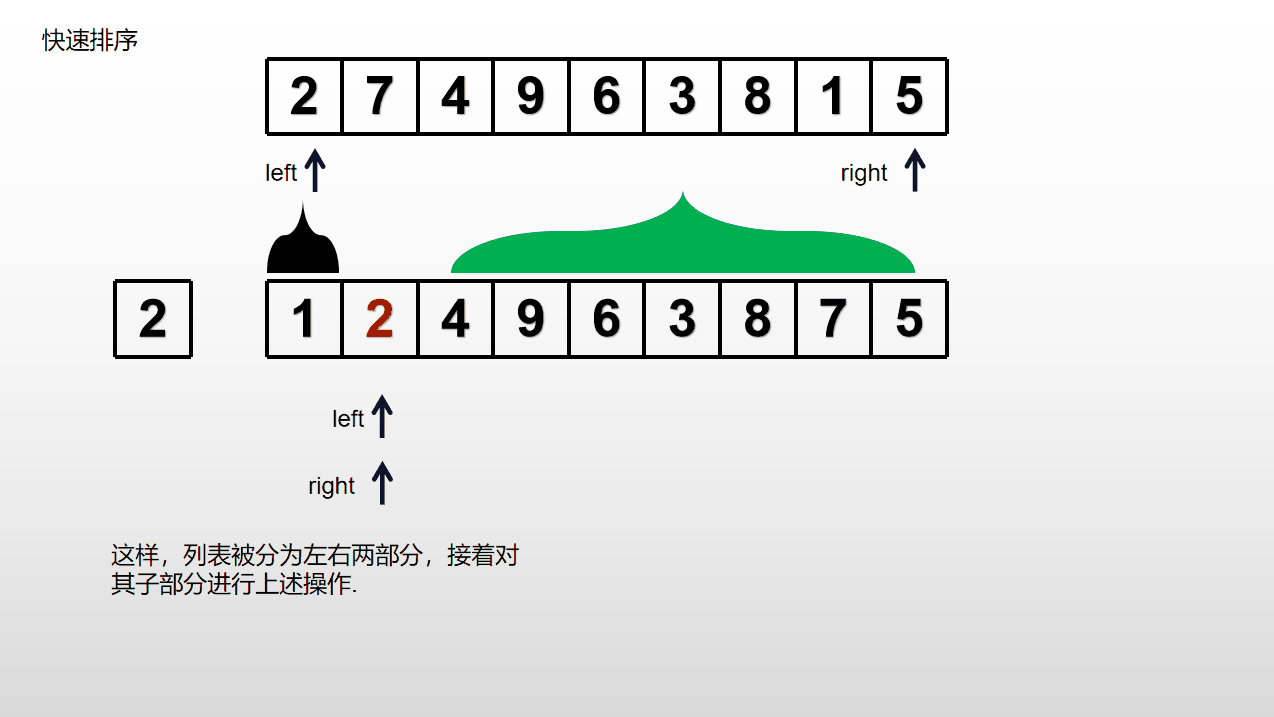
 分为两个部分后，若一个部分中只有一个或0个元素则该部分不用进行上述操作，否则一直进行上述操作。

代码如下：

def partition(ls, left, right):
    '''
    具体实现的代码
    ls:输入列表
    left:左指针
    right:右指针
    '''
    temp = ls[left]            #取出基准元素
    
    while left < right:        #保证左指针在右指针左侧， 这是大前提

        #循环中指针是在移动，当左右指针重合时表示该结束循环了
        while left < right and ls[right] >= temp:  
            right -= 1         #右侧元素大于基准元素时，应左移判断下一个
        #当左右指针重合时或者找到小于基准的数时，将其赋值到空位处
        ls[left] = ls[right]
        
        #此处判断位置作用同上
        while left < right and ls[left] <= temp:
            left += 1           #左侧元素小于基准元素时，右移判断下一个
        #当左右指针重合或找到大于基准元素的数时，将其赋值到空位处
        ls[right] = ls[left]
    #最后左右指针一定是重合的，此时列表已经分为两部分，基准元素恰好处在中间位置此时将其填充至左右指针出均可
    ls[left] = temp
    
    return left                  #返回基准元素的位置，列表被此位置一分为二


def quick_sort(ls, left, right):
    if left < right:                            #至少两个元素
        mid_index = partition(ls, left, right)    #找出基准元素应该放在那，然后将列表一分为二
        quick_sort(ls, left, mid_index-1)        #递归调用本身，计算基准元素左侧列表的顺序
        quick_sort(ls, mid_index+1, right)       #递归调用本身，计算基准元素右侧列表的顺序

ls = [2, 7, 4, 9, 6, 3, 8, 1, 5]
quick_sort(ls, 0, len(ls)-1)
print(ls)


#############
[1, 2, 3, 4, 5, 6, 7, 8, 9]

堆排序

需要有“树”的先验知识，这里的堆是基于完全二叉树的一种特殊结构。

• 大根堆：一颗完全二叉树，且任一节点的值都大于其子节点
• 小根堆：一颗完全二叉树，且任一节点的值都小于其子节点

堆排序是基于堆的向下调整进行的排序，具体的流程如下动图：

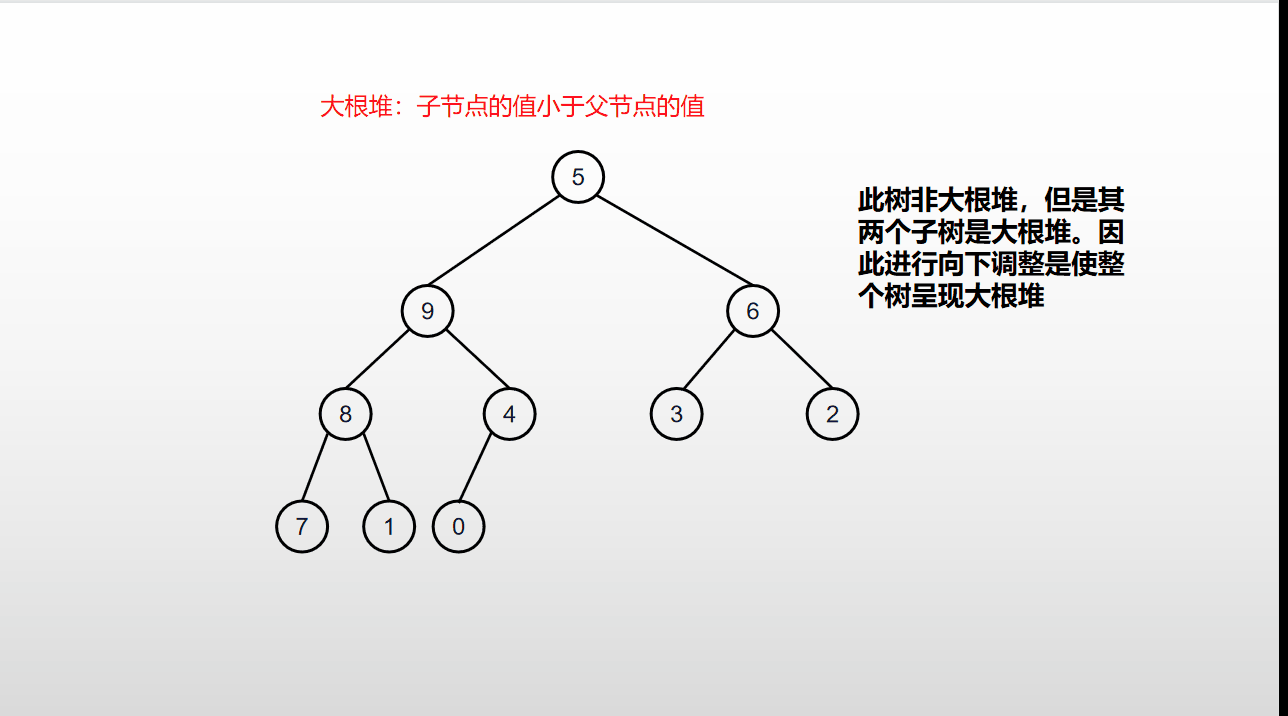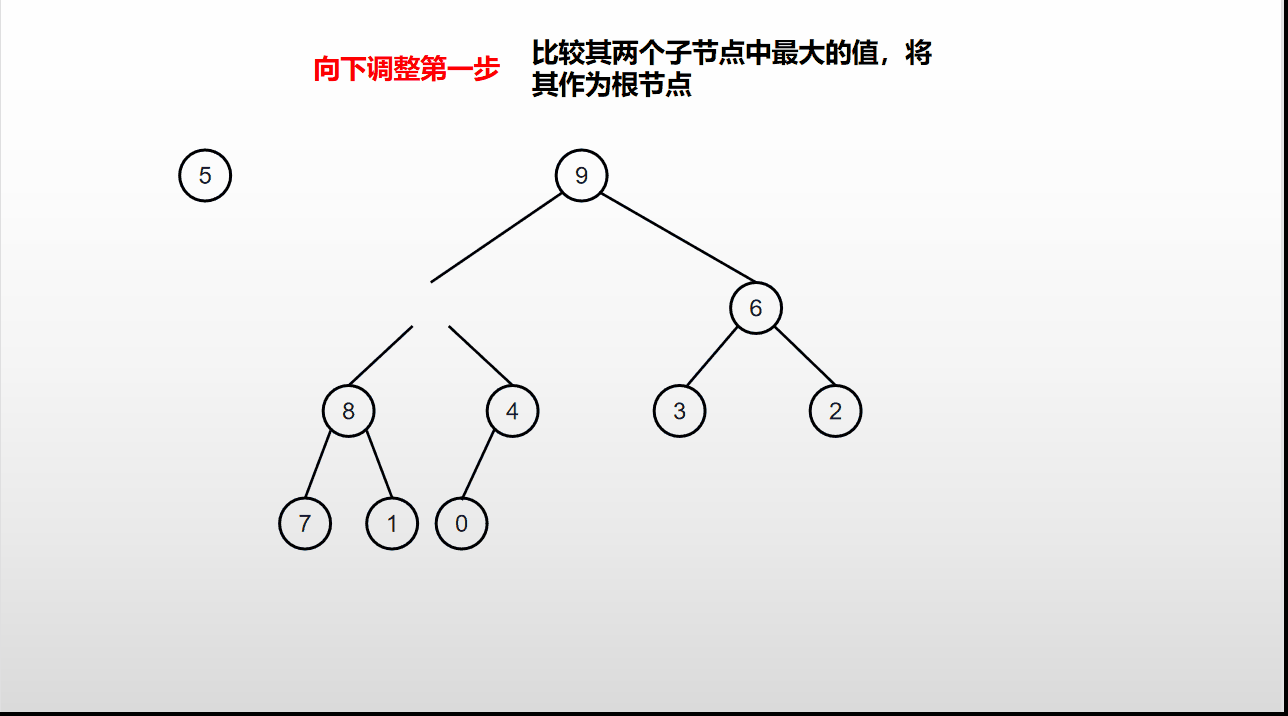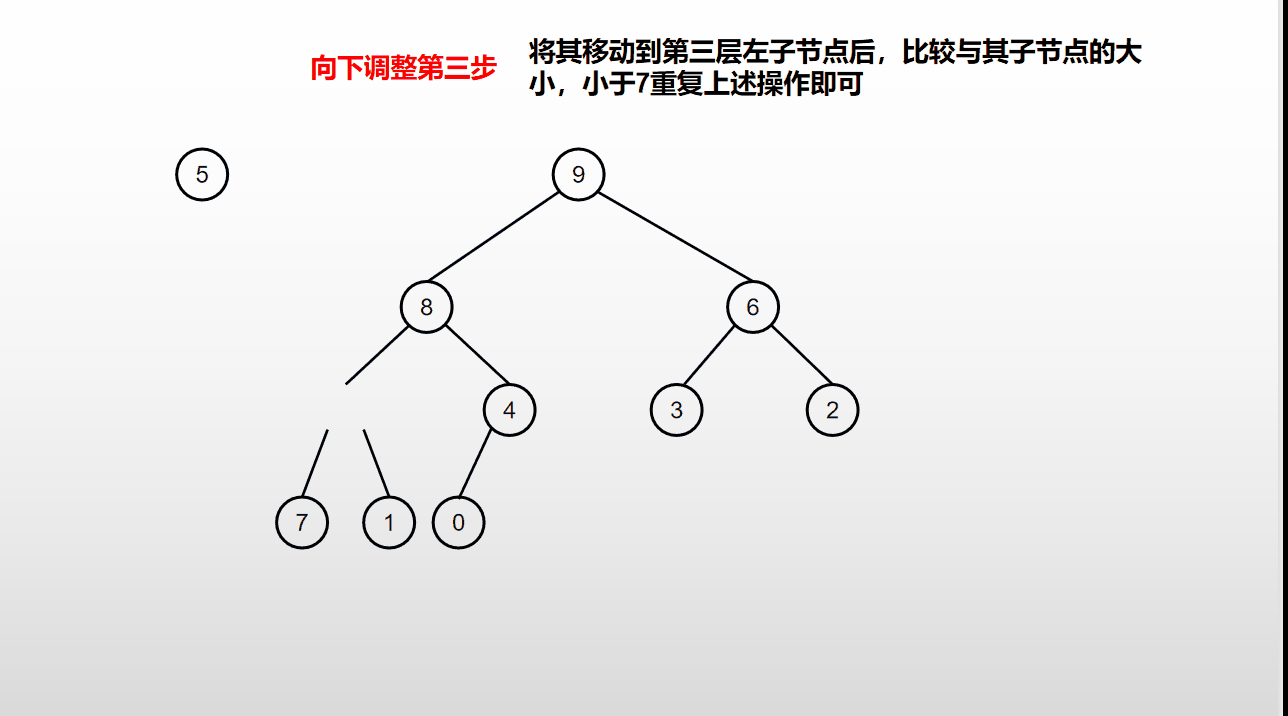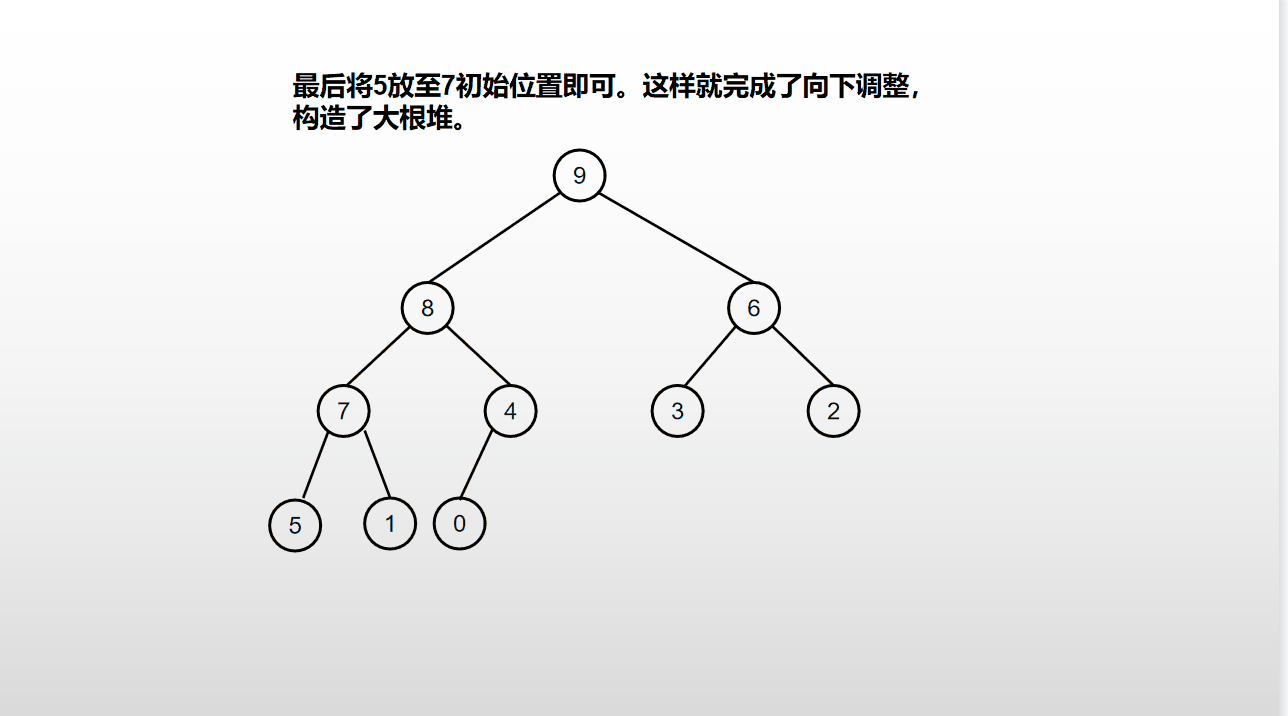
 堆排序过程：

1. 通过向下调整构建大根堆；
2. 得到堆顶元素为最大元素，去除堆顶（取出）；
3. 将最后一层组后一个叶子元素放到堆顶，然后向下调整使堆重新变得有序；
4. 完成调整后又成为大根堆；
5. 重复上述操作，直到堆变为空。

不使用递归代码：

import random

def heapify(ls, low, high):

    '''
    调整函数

    low:堆的根节点
    heigh:堆最后一个元素的位置
    '''
    i = low                 # i从根节点开始
    j = 2 * i + 1           # j指向i的左子节点
    temp = ls[low]          # 暂存堆顶元素

    while j <= high:        # 当子节点未超出节点数时，进行调整
        if j + 1 <= high and ls[j + 1] > ls[j]:
        #j+1指向i的右子节点，当右子节点元素值大于左子节点时，则选中右子节点那一分支进行后续比较
            j = j + 1       #指向右子节点
        if ls[j] > temp:    #当i的两个子节点元素的值大于i所在元素时，用较大值进行替换
            ls[i] = ls[j]
            i = j           #此时，还需要判断较大值所在节点的子节点的值是否比i的值大，相当于向下移一层接着调整
            j = i * 2 + 1   #新的左子节点，如果满足条件继续循环
        else:               #与上一个if一套，当ls[j]<=temp时，无需对i（父节点）进行操作。（表明此堆符合大根堆）
            break
    else:
        ls[i] = temp        #当j>high时，表示i无子节点了，此时将最初的元素放在该位置上即可

def heap_sort(ls):
    '''
    堆排序函数
    '''
    n = len(ls)
    #首先构建大根堆
    for i in range((n - 2) // 2, -1, -1):    #根据最后一层最后一片叶子，找其父节点进行调整，之后依次向左向上进行，直至找到根节点
        heapify(ls, i, n-1)
    #构建大根堆完成，进行排序

    for j in range(n - 1, -1, -1):          #j指向最后一层最后一片叶子元素，存放堆顶元素，节省存储空间
        ls[0], ls[j] = ls[j], ls[0]         #对顶元素为最大值，直接将其存放到最后叶子处
        heapify(ls, 0, j - 1)               #取出最大值后，在次进行调整，此时最后的叶子不需要考虑（是最大值）所以最后元素为j-1




ls = [i for i in range(10)]
random.shuffle(ls)

print(ls)

heap_sort(ls)
print(ls)




+++++++++++++++++++++++++++++
[7, 6, 0, 8, 1, 2, 4, 5, 3, 9]
[0, 2, 3, 3, 4, 5, 8, 9, 9, 9]

使用递归调用自身代码：