2021-05-08

多功能：

房价预测问题中，房价只与面积有关，可是这并不符合事实，房价的因素与许多因素有关，所以我们引入多功能。
（会用到线代的基础知识）

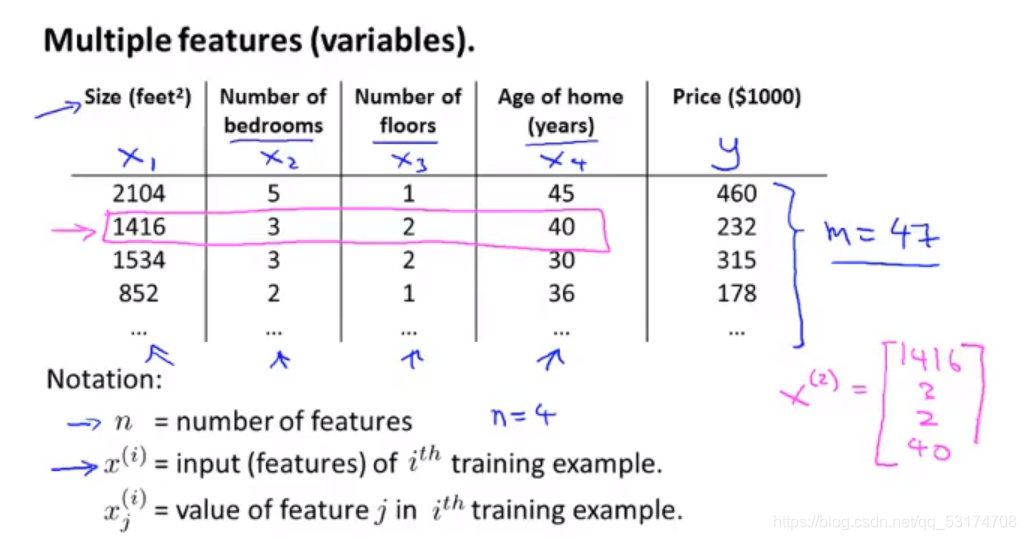
所以特征量多的时候可以采用下面这种方法：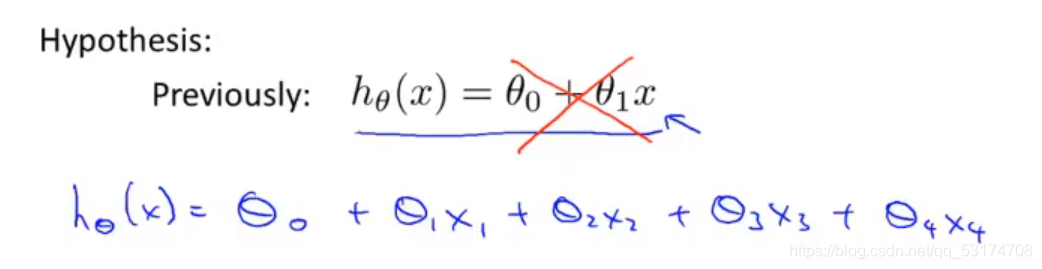
话不多说，先看图：
线性代数的行列式乘积表示一一对应，为了满足对应，设X0=1，这样不影响大小的情况下增加了一个特征向量，有x=和θ=,可以看到，为了使两个行列式相乘，用到了转置。
好了，既然单一特征值可以梯度下降，多个特征值也可以有——多元梯度下降：

多元梯度下降：

其实多元梯度下降在我看来，无非就是增加了维度，设想平面上的曲线我们靠导数，立体图上成为了偏导，无非就是在坐标轴方向上求偏导，其他参数视为常数消去而已（如果我理解错了，评论区滴滴我），

def gradientFunction(W):#梯度功能
    w1, w2 = W
    w1_grad = 2 * w1 + 2 * w2
    w2_grad = 2 * w2 + 2 * w1

这是二元函数f(w1,w2) = w1² + w2² + 2w1w2 + 500的偏导数，增加了特征值，为非就是增加了偏导数方程的数量。
特征和多项式回归
我们继续研究房价问题，例如影响房价的因素我们暂定为两个，房子宽度和长度，这很明显是两个特征值，如果换一个角度去思考，这不就是面积吗？所以两个特征值就成了一个特征值。（但是面积相同房子纵横比却并不相同，这里仅提供一种思路）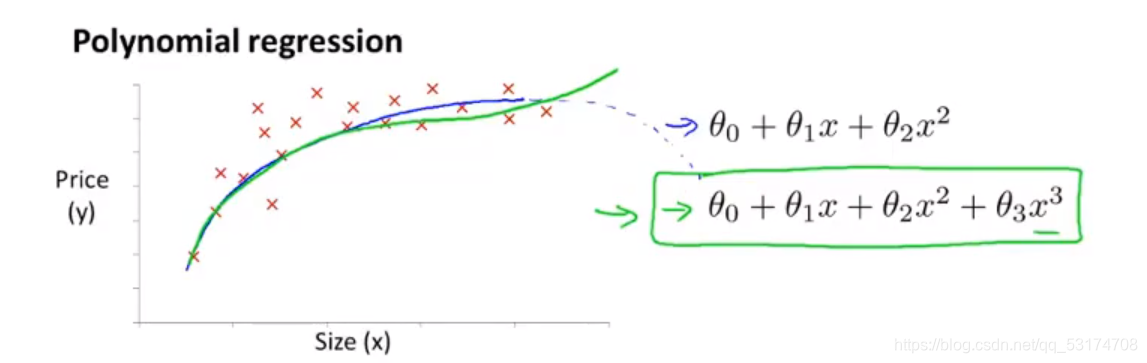
然后拟合我们的点，为了更高的精度，选择更高的阶数，随之而来的可能是过拟合问题。
其实，不光可以升阶，还可以降，如下

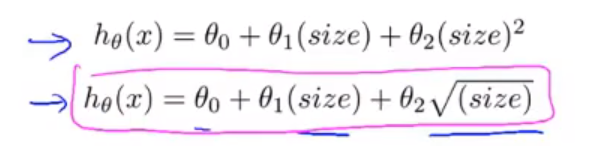
你可以自由选择使用什么特征，并且通过设计不同的特征，你能够用更复杂的函数拟合数据，而不是只用一条直线去拟合，特别是你也可以用多项式函数，有时从合适的角度来寻找特征，你就能得到一个更符合你数据的模型。