递归与递推

递归与递推

AcWing 92. 递归实现指数型枚举

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N =20;
int n;
int st[N];
void dfs(int u)
{
    if(u>n)
    {
        for(int i=1;i<=n;i++)
            if(st[i]==1)
                cout<<i<<' ';
        cout<<endl;
        return;
    }
        st[u]=2;
        dfs(u+1);
        st[u]=0;

        st[u]=1;
        dfs(u+1);
        st[u]=0;

}
int main()
{
    cin>>n;
    dfs(1);
    return 0;   
}

AcWing 94. 递归实现排列型枚举

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=10;
int path[N];//0表示还没放数 1~n表示放了哪个数
bool st[N];//true 表示用过 ， false表示还没用过
int n;
void dfs(int u)
{
    if(u>n)//边界
    {
        for(int i=1;i<=n;i++)
            cout<<path[i]<<' ';
        cout<<endl;
        return;
    }
    //依次枚举每个分支,即当前每个位置可以填那些数
    for(int i=1;i<=n;i++)
    {     
        if(!st[i])
        {
            st[i]=true;
            path[u]=i;
            dfs(u+1);
            
            //path[u]=0; 恢复现场 因为下次会直接覆盖掉path[i]的值
            st[i]=false;//恢复现场
        }
        
    }
}
int main(int u)
{
    cin>>n;
    dfs(1);
    return 0;
}

AcWing 93. 递归实现组合型枚举

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=30;
int n,m;
int path[N];
int start;
void dfs(int u,int start)
{   
    if(u+n-start<m) //剪枝 n-1+n-start+1<m  n-1为当前选了几个数 n-start+1为还剩几个数可用 如果加起来小于要选的个数 即不成立
        return;
    if(u==m+1)
    {
        for(int i=1;i<=m;i++)
            cout<<path[i]<<' ';
        cout<<endl;
        return;
    }
    
    for(int i=start;i<=n;i++)
    {
        path[u]=i;
        dfs(u+1,i+1);
        //path[u]=0; 恢复现场
    }
}
int main()
{
    cin>>n>>m;
    dfs(1,1);
    return 0;
}

AcWing 1208. 翻硬币

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;

const int N=110;

int main()
{
    string s1;
    string s2;
    cin>>s1>>s2;
    int res=0;
    for(int i=0;i<s1.length()-1;i++)//枚举到长度-1,因为一定有解 最后一个的状态是由前一个确定的
    {
       if(s1[i]!=s2[i])
       {
        //   if(s1[i]=='*') s1[i]='o'; 其实不用翻转这一个 直接翻转下一个即可 依次往后看
        //   else s1[i]='*';

           if(s1[i+1]=='*') s1[i+1]='o';
           else s1[i+1]='*';
           res++;
       }
    }
    cout<<res<<endl;
    return 0;
}

AcWing 95.费解的开关

思路：
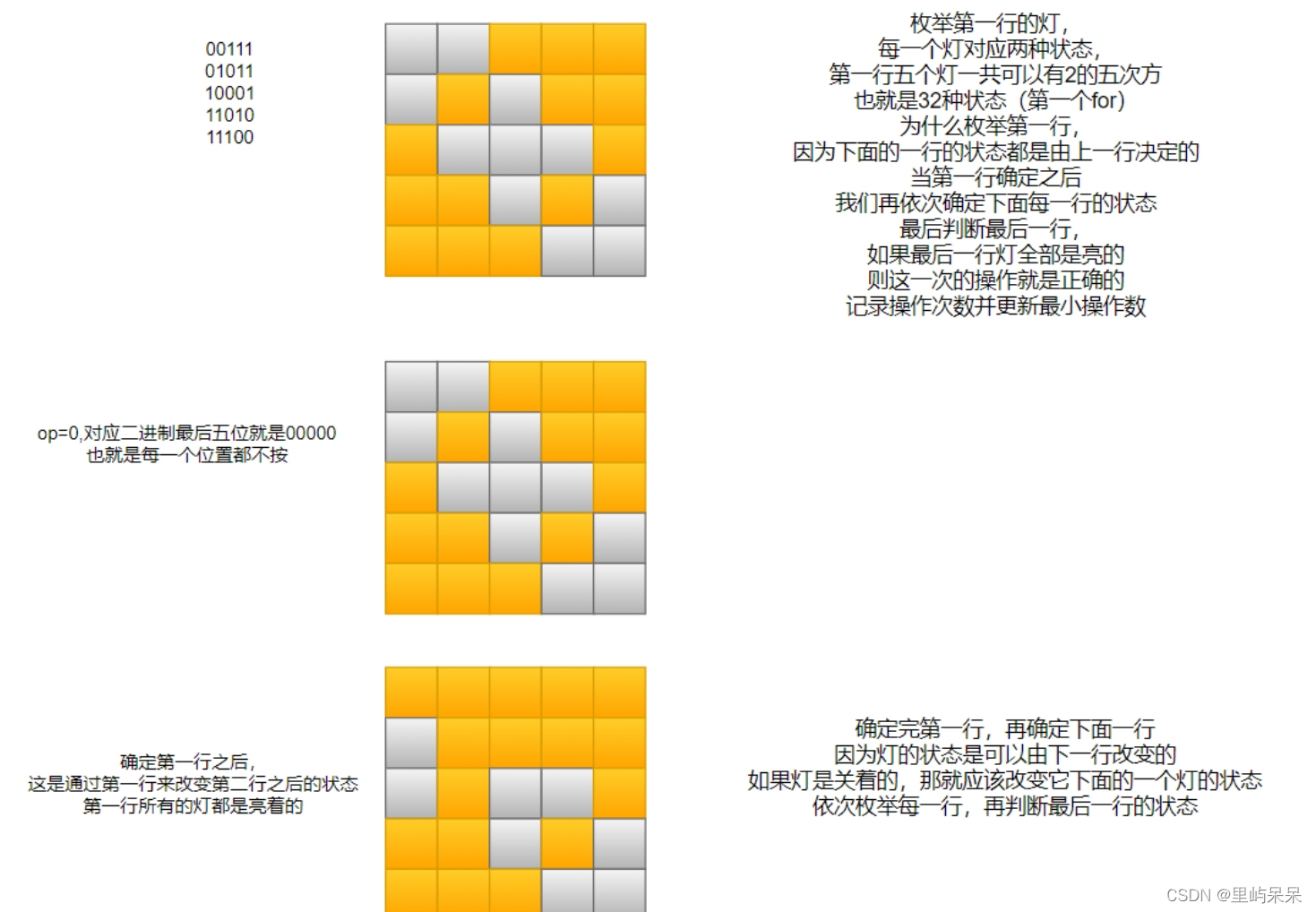
可以枚举第一行的灯，每一个灯对应两种状态（开/关），第一行五个灯一共有2的五次方也就是32种状态（第一个for循环）
为什么枚举第一行？因为下面的一行状态都是由上一行决定的，当第一行确定之后，我们再依次确定下面的每一行的状态，最后判断最后一行的灯，如果最后一行全部都是亮的，那么这一次操作就是正确的，记录操作次数并更新最小的操作数

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;

const int N=6;//开大一点儿 因为字符数组以换行结尾
char g[N][N],back[N][N];
int dx[5]={0,0,-1,1,0};//dx,dy依次对应 右、左、上、下、自己（当前拨动的开关）
int dy[5]={1,-1,0,0,0};

int n;
void turn(int a,int b)
{
    for(int i=0;i<5;i++)
    {
        int x=a+dx[i];
        int y=b+dy[i];
        if(x<0 || y<0 || x>=5 || y>=5) //出界
            continue;
        g[x][y]^=1;//因为0和1的编码对应的二进制只有最后一位不一样，差1 0异或1就是1
    }       
}
int main()
{
    cin>>n;
    while(n--)
    {
        int res=10;//其实大于6步就不合格了 用来更新状态
        int step=0;
        for(int i=0;i<5;i++)
            for(int j=0;j<5;j++)
                cin>>g[i][j];
        
        for(int i=0;i<32;i++)
        {//枚举第一行的32种状态，每种状态都可能对应一种结果，从中找出来操作数最小的
            step=0;
            //拷贝一份，下一次枚举的时候还用原来的数组
            memcpy(back,g,sizeof(g));
            for(int j=0;j<5;j++)
            {//j代表第一行的五个灯 当前位置为'0'表示不操作，为'1'表示操作
                if(i>>j&1)//位运算操作看第j位是否为0  j从0开始
                {
                    step++;//记录操作步数
                    turn(0,j);//改变这个灯和相邻四个灯的状态
                }
            }
            for(int i=0;i<4;i++)//枚举前四行
            {
                for(int j=0;j<5;j++)//每行5个灯
                {
                    if(g[i][j]=='0')//如果这个灯是关的，就改变它下面的灯
                    {
                        step++;
                        turn(i+1,j);
                    }
                }
            }
            
            bool dark=false;//用来判断最后是否成功
            for(int i=0;i<5;i++)
                for(int j=0;j<5;j++)//遍历最后一行灯的状态
                    if(g[4][j]=='0')//如果有不亮的的灯说明这一组操作数不能使灯全部变亮
                    {
                        dark =true;
                        break;
                    }
                    
            if(!dark) res=min(res,step);//如果灯全亮 更新操作数最小值
            memcpy(g,back,sizeof back);//还原g数组
        }
        if(res>6) cout<<-1<<endl;
        else cout<<res<<endl;
    }
    return 0;
}