克鲁斯卡尔（Kruskal）算法

克鲁斯卡尔算法是用来干什么的？ 用于生成最小生成树

那么最小生成树又是什么？ 最小生成树的定义：连通图G上的一棵各边权值之和最小的带权生成树

算法思想：

假设G是一个具有n个顶点的连通图，T是一个拥有图G的所有顶点，但不含任何边的图。将图G中的边按照权值从小到大依次选取，如果选取的边不会使图T形成回路，则使这条边成为图T中的一条边，如此进行下去，直到图T包含n-1条边，此时的图T就是图G的最小生成树。

举个例子，图G如下图，求它的最小生成树

将图G中的边按照权值从小到大依次选取，如果选取的边不会使图T形成回路，则使这条边成为图T中的一条边

当操作到第6步时，图T就是图G的最小生成树

这个算法的关键在于如何判断选取的边是否会使图T形成回路，我们又可以转化为判断这条边的两个顶点u,v是否在同一棵树上，也就是判断顶点u,v的根结点是否相同
所以我们可以设计一个SeekRoot函数，用它来求顶点所在树的根结点。如果两个顶点的根结点不同，则说明我们可以选取这条边，它不会使图T形成回路。
这时候我们还需要用到一个辅助数组set，用来存放各个顶点母亲结点

源代码

# include <stdio.h>
# define MAX 100
# define MAXLEN 100


typedef struct
{
	int u;
//边的起点	
	int v;
//边的终点	
	int w;
//顶点u和顶点v所形成的边的权值	
}Edge;


Edge E[MAX];
//定义全局变量
//为什么要创建一个数组？方便操作 


//创建一个无向网的边表 
int CreateEdge ()
{
	int n;
//n表示边长
    int i;
    printf ("请输入无向网的边数：");
    scanf ("%d", &n); 
    printf ("请分别输入顶点u,v和相应的权值w！\n输入格式为：(数字 数字 数字)\n");
    for (i = 0; i < n; i++)
    {
    	printf ("u v w =");
	    scanf ("%d %d %d", &E[i].u, &E[i].v, &E[i].w);
	}
	return n;
//返回边数	 	
}


//根据权值从小到大给数组排序 
int Sort (int n)
{
	int i, j;
	Edge t;
	
//如果前一个顶点的权值比后一个顶点的权值大，则交换这两个顶点的的值	
	for (i = 0; i < n-1; i++)
	{
		for (j = i+1; j < n; j++)
		{
			if (E[i].w > E[j].w)
			{
				t = E[i];
				E[i] = E[j];
				E[j] = t;
			} 
		}
	}
} 


//寻找顶点v所在树的根节点 
int SeekRoot (int Set[], int v)
{
	int i = v;
	while (Set[i] != 0)
	{
		i = Set[i];
	}
	return i;
//返回顶点v所在树的根节点
} 


void Kurskal (int n)
{
	int i;
	int v1, v2;
	int Set[MAXLEN];
	for (i = 0; i < n; i++)
	{
		Set[i] = 0;
	}
//给树的根节点初始化	
	
	i = 0;
	printf ("\n最小生成树为：\n");
	while (i < n)
	{
		v1 = SeekRoot (Set, E[i].u);
//v1为E[i].u的根节点		
		v2 = SeekRoot (Set, E[i].v);
//v2为E[i].v的根节点		
		if (v1 != v2)
//如果v1和v2的根节点不相等，即v1,v2不在同一棵树上时		
		{
		   	printf ("(%d,%d) %d\n",E[i].u, E[i].v, E[i].w);
		    Set[v1] = v2;
//合并两棵树，使新的树的根结点为v2		    
		}
		i++;
	}       
}


int main (void)
{
	int n;
	n = CreateEdge ();
	Sort (n);
	Kurskal (n);
	return 0;
}

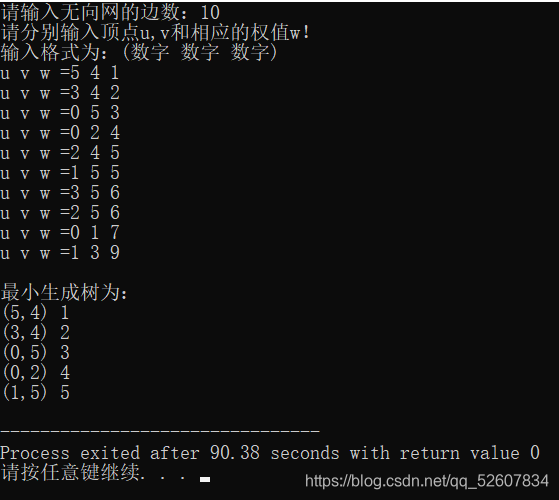
运行结果