经典算法之希尔排序法（Java实现）

最新推荐文章于 2025-04-21 09:47:56 发布

顾老师不懂代码

最新推荐文章于 2025-04-21 09:47:56 发布

阅读量1.3k

点赞数 11

分类专栏： # 算法之路文章标签：经典算法排序 Java

本文链接：https://blog.youkuaiyun.com/qq_52487066/article/details/126331729

版权

算法之路专栏收录该内容

14 篇文章

订阅专栏

活动地址：21天学习挑战赛

一、算法

1.算法概述

希尔排序法又称为缩小增量排序法，是一种基于插入思想的排序方法。它是直接插入排序法的进一步优化的算法，使得排序的性能有了一个极大的飞跃！

2.基本思想

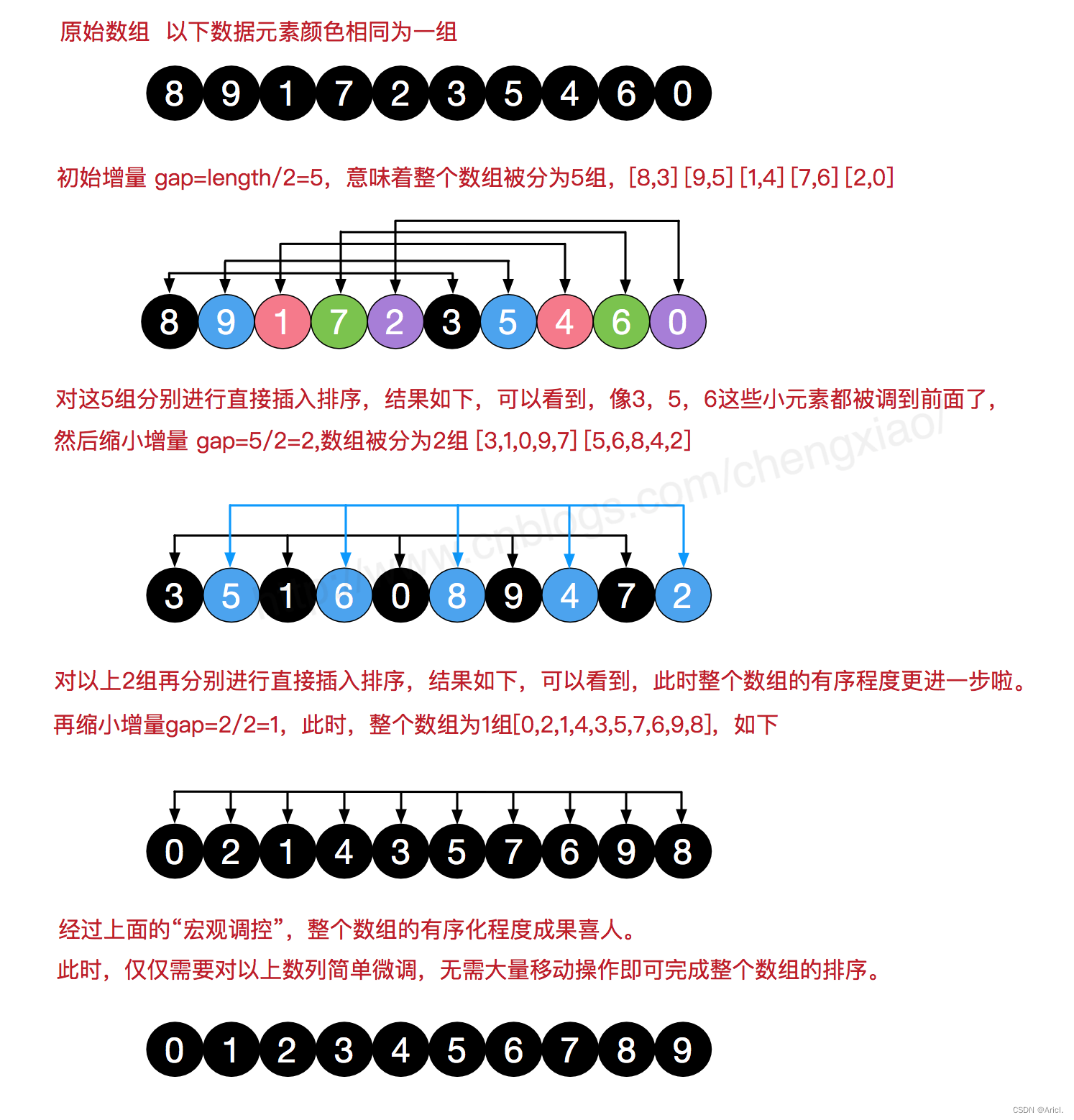
希尔排序法的伟大之处在于很好的利用了直接插入法的最佳性质：待排序记录较少且基本有序。所以希尔排序法的思路是将待排序的序列按照增量递减的方式分成若干个组，将原来较大的序列不断切割成一个个小的子序列，使子序列符合“数目少且基本有序”这一条件，然后分别对各个子序列进行直接插入排序，经过上述的操作后，使得整个序列已经基本有序，然后对整个序列进行一次直接插入排序，即可得到一个整体有序的序列，排序完成！

往期相关文章传送门：

3.算法步骤

第一趟取增量为d1（d1<n）把全部记录分成若干组，所有间隔距离为d1的分在同一组，在各个组内进行直接插入排序
第二趟去增量d2(d2<d1)，重复上述的分组与排序
依次类推，不断缩小所取的增量d，直到所有记录在同一组中，此时所有记录已经基本有序了，再整体使用一次直接插入排序法即可完成排序

（注：图片来自网络）

4.算法特点

记录跳跃式的移动导致希尔排序方法是不稳定排序法
只能适用于顺序结构，不能用于链式结构
增量序列可以有多种取法，但应该使增量序列中的值没有除1之外的公因子，并且逐渐缩小增量后，最后的增量值必须为1
记录总的比较次数和移动次数都比直接插入排序要少，当n越大时，效果越明显。
希尔排序法适合初始记录无序、n较大的情况

二、算法实践

1.Java代码

package TwentyOne_Challenge;

public class DaySeven {
    public static void main(String[] args) {
        int []a={3,38,5,44,15,36,26,27,2,47,46,4,19,50,48,100};
        System.out.print("原来序列如下：");
        for (int i = 0; i <a.length ; i++) {
            System.out.print(a[i]+" ");
        }
        sort(a);
        System.out.println();
        System.out.print("经过希尔排序后：");
        for (int i = 0; i <a.length ; i++) {
            System.out.print(a[i]+" ");
        }
    }
    private static  void sort(int arr[]) {
        int n=arr.length,d = n;
        while (d>1) {
            //每次对增量d进行折半
            d/=2;
            //单趟排序
            for (int i = 0; i < n - d; i++) {
                int right = i;
                int temp = arr[right + d];//存储待排序元素
                while (right >= 0) {
                    if (temp < arr[right]) {
                        //组内排序
                        arr[right + d] = arr[right];
                        //组内的下一元素，从右往左
                        right -= d;
                    }
                    else {
                        break;
                    }
                }
                //如果组内某一对元素已经有序则无需交换，将存储的待排序元素重新赋给原值
                arr[right + d] = temp;
            }
        }
    }
}