Dp的补充

一、2. 01背包问题 - AcWing题库

二、3. 完全背包问题 - AcWing题库

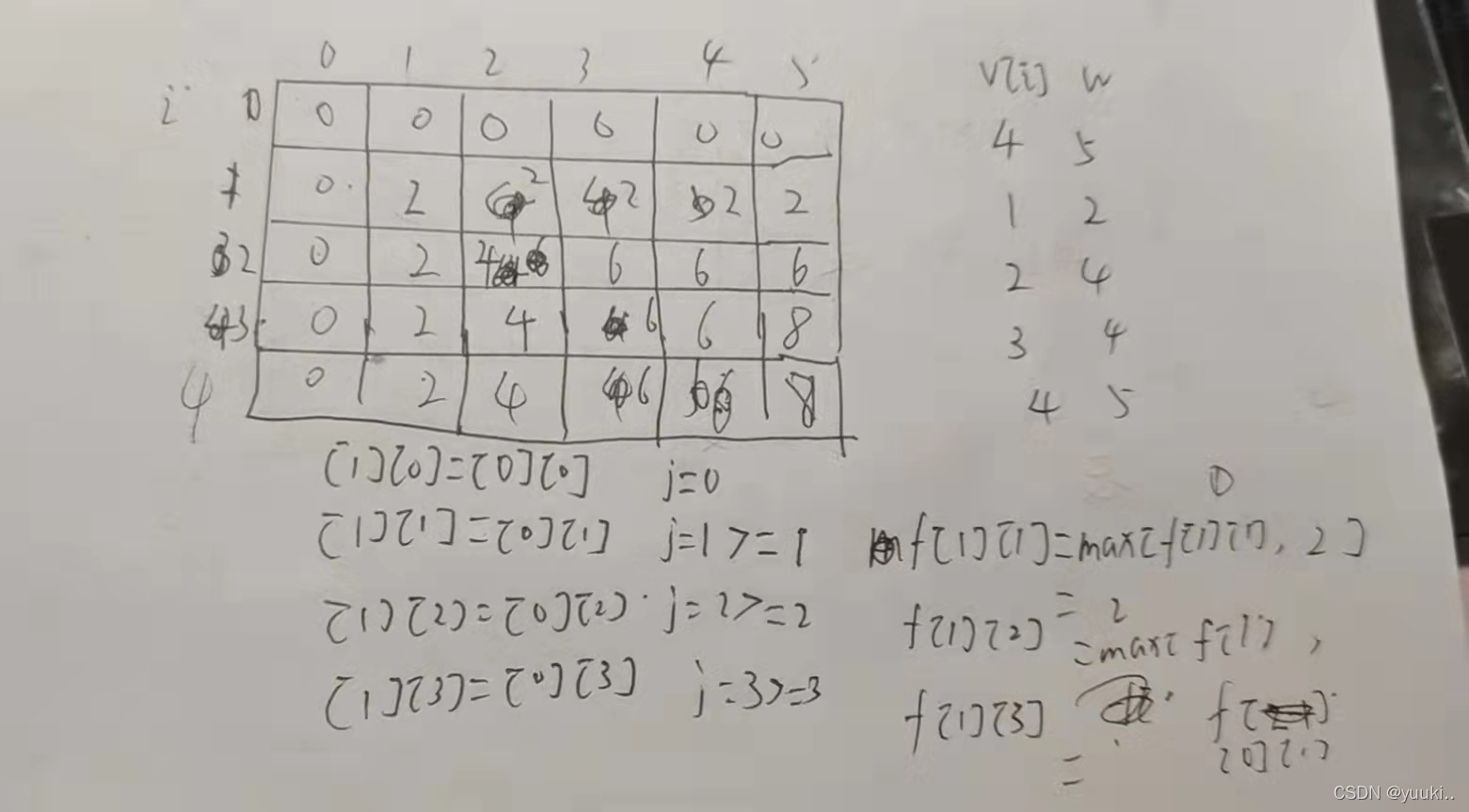
1、朴素算法（一般都会超时）

#include<bits/stdc++.h>
using namespace std;
const int N=10010;
int n,m;
int v[N],w[N];
int f[N][N];
int main()
{
    cin>>n>>m;
    for(int i=1;i<=n;i++) cin>>v[i]>>w[i];
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=m;j++)
        {
            for(int k=0;k*v[i]<=j;k++)
            {
                f[i][j]=max(f[i][j],f[i-1][j-v[i]*k]+w[i]*k);
            }
        }
    }
    cout<<f[n][m]<<endl;
    return 0;
}

2、二维优化

#include<bits/stdc++.h>
using namespace std;
const int N=10010;
int n,m;
int v[N],w[N];
int f[N][N];
int main()
{
    cin>>n>>m;
    for(int i=1; i<=n; i++)
        cin>>v[i]>>w[i];
    for(int i=1; i<=n; i++)
    {
        for(int j=0; j<=m; j++)
        {
            f[i][j]=f[i-1][j];
            if(j>=v[i]) f[i][j]=max(f[i][j],f[i][j-v[i]]+w[i]);
        }
    }
    cout<<f[n][m]<<endl;
    return 0;
}

3、一维优化

#include<bits/stdc++.h>
using namespace std;
const int N=10010;
int n,m;
int v[N],w[N];
int f[N];
int main()
{
    cin>>n>>m;
    for(int i=1; i<=n; i++)
        cin>>v[i]>>w[i];
    for(int i=1; i<=n; i++)
    {
        for(int j=v[i]; j<=m; j++)
        {
            f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    }
    cout<<f[m]<<endl;
    return 0;
}

​​​​​​

for (int i=1;i<=n;++i) {
    for (int j=v[i];j<=m;++j)    
	    f[j] = max(f[j], f[j-v[i]] + w[i]);}

for (int i=1;i<=n;++i) {
    for (int j=m;j>=v[i];--j)    
	    f[j] = max(f[j], f[j-v[i]] + w[i]);}

三、4. 多重背包问题 I - AcWing题库

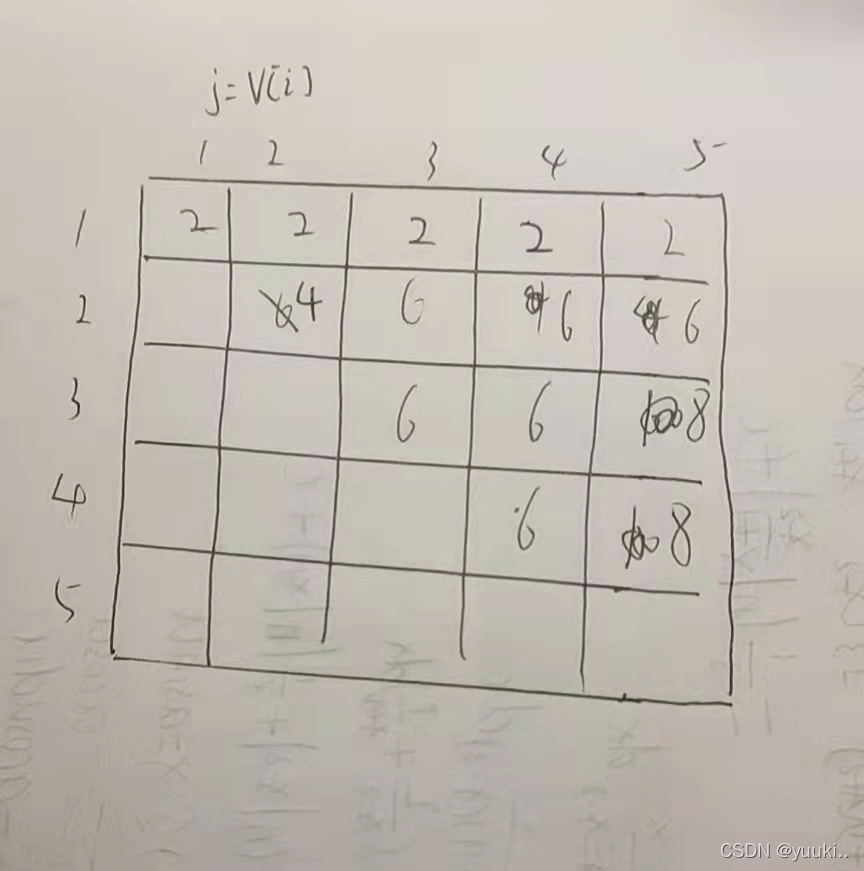
1、朴素算法

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 110;
int n, m;
int w[N],v[N],s[N];
int f[N];

int main() {
    cin >> n >> m;
    for (int i=1;i<=n;++i)  
    {
        cin>>v[i]>>w[i]>>s[i];
    }
    
    for (int i=1;i<=n;++i) {
        for (int j=m;j>=0;--j) {
	        for (int k=1; k<=s[i] && k*v[i] <= j; ++k) {
		        f[j] = max(f[j], f[j-k*v[i]]+k*w[i]);
		    }
        }
    }
    
    cout << f[m] << endl;
    return 0;
}

但是这个朴素方法在下面背包就会超时

2、二进制优化

如果用这个的话

for (int i=1;i<=n;++i) {
    for (int j=m;j>=v[i];--j) { 
        f[j] = max(f[j], f[j-v[i]] + w[i], f[j-2*v[i]] + 2*w[i], f[j-3*v[i]] + 3*w[i], ...);
        //这里就是再用一重循环

还是不可以

所以用二进制优化，就是二进制可以表示出一定范围内的任意的数

#include<bits/stdc++.h>
using namespace std;
const int N=2500;
int f[N];
int v[N],w[N];
int n,m;
int main()
{
    cin>>n>>m;
    int cnt=0;
    for(int i=1;i<=n;i++)
    {
        int a,b,s;
        cin>>a>>b>>s;
        int k=1;
        while(k<=s)
        {
             cnt++;
             v[cnt]=a*k;
             w[cnt]=b*k;
             s-=k;
             k*=2;
        }
        if(s>0)
        {
            cnt++;
            v[cnt]=a*s;
            w[cnt]=b*s;
        }
    }
    n=cnt;
    for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=v[i];j--)
        {
            f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    }
    cout<<f[m]<<endl;
    return 0;
}

四、5. 多重背包问题 II - AcWing题库

N的大小要开大一点，原因是多个物品，不可以像上面那种开小，否则不对

#include<bits/stdc++.h>
using namespace std;
const int N=250000;
int f[N];
int v[N],w[N];
int n,m;
int main()
{
    cin>>n>>m;
    int cnt=0;
    for(int i=1;i<=n;i++)
    {
        int a,b,s;
        cin>>a>>b>>s;
        int k=1;
        while(k<=s)
        {
             cnt++;
             v[cnt]=a*k;
             w[cnt]=b*k;
             s-=k;
             k*=2;
        }
        if(s>0)
        {
            cnt++;
            v[cnt]=a*s;
            w[cnt]=b*s;
        }
    }
    n=cnt;
    for(int i=1;i<=n;i++)
    {
        for(int j=m;j>=v[i];j--)
        {
            f[j]=max(f[j],f[j-v[i]]+w[i]);
        }
    }
    cout<<f[m]<<endl;
    return 0;
}

九、9. 分组背包问题 - AcWing题库

#include<bits/stdc++.h>
using namespace std;
const int N=2500;
int f[N];
int n,m;
int v[N][N],w[N][N],s[N];
int main()
{
   cin>>n>>m;
   for(int i=1;i<=n;i++)
   {
       cin>>s[i];
       for(int j=0;j<s[i];j++)
       {
           cin>>v[i][j]>>w[i][j];
       }
   }
   for(int i=1;i<=n;i++)
   {
       for(int j=m;j>=0;j--)
       {
           for(int k=0;k<s[i];k++)
           {
               if(v[i][k]<=j)
               {
                   f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);
               }
           }
       }
   }
    cout<<f[m]<<endl;
}

这道题的重点就是背包的只可以拿一个，它无论一组多少个东西，它只可以拿一个东西。


898. 数字三角形 - AcWing题库

#include<bits/stdc++.h>
using namespace std;
const int N=1000;
int f[N][N];
int v[N][N],w[N][N];
int n;
int a[N][N];
int INF=1e9;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        for(int j=1;j<=i;j++)
        {
            cin>>a[i][j];
        }
    }
    for(int i=1;i<=n;i++)
    {
        for(int j=0;j<=i+1;j++)
        {
            f[i][j]=-INF;
        }
    }
    f[1][1]=a[1][1];
    for(int i=2;i<=n;i++)
    {
        for(int j=1;j<=i;j++)
        {
            f[i][j]=max(f[i-1][j-1],f[i-1][j])+a[i][j];
        }
    }
    int res=-INF;
    for(int i=1;i<=n;i++)
    {
        res=max(res,f[n][i]);
    }
    cout<<res<<endl;
}

这个题目的重点是三角形转换成了直角三角形

895 最长上升子序列

#include<bits/stdc++.h>
using namespace std;
const int N=1000;
int a[N],f[N];
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        cin>>a[i];
    }
    for(int i=1;i<=n;i++)
    {
        f[i]=1;
        for(int j=1;j<i;j++)
        {
            if(a[j]<a[i])
            {
                f[i]=max(f[i],f[j]+1);
            }
        }
    }
    int res=0;
    for(int i=1;i<=n;i++)
        res=max(res,f[i]);
    cout<<res;
    return 0;
}

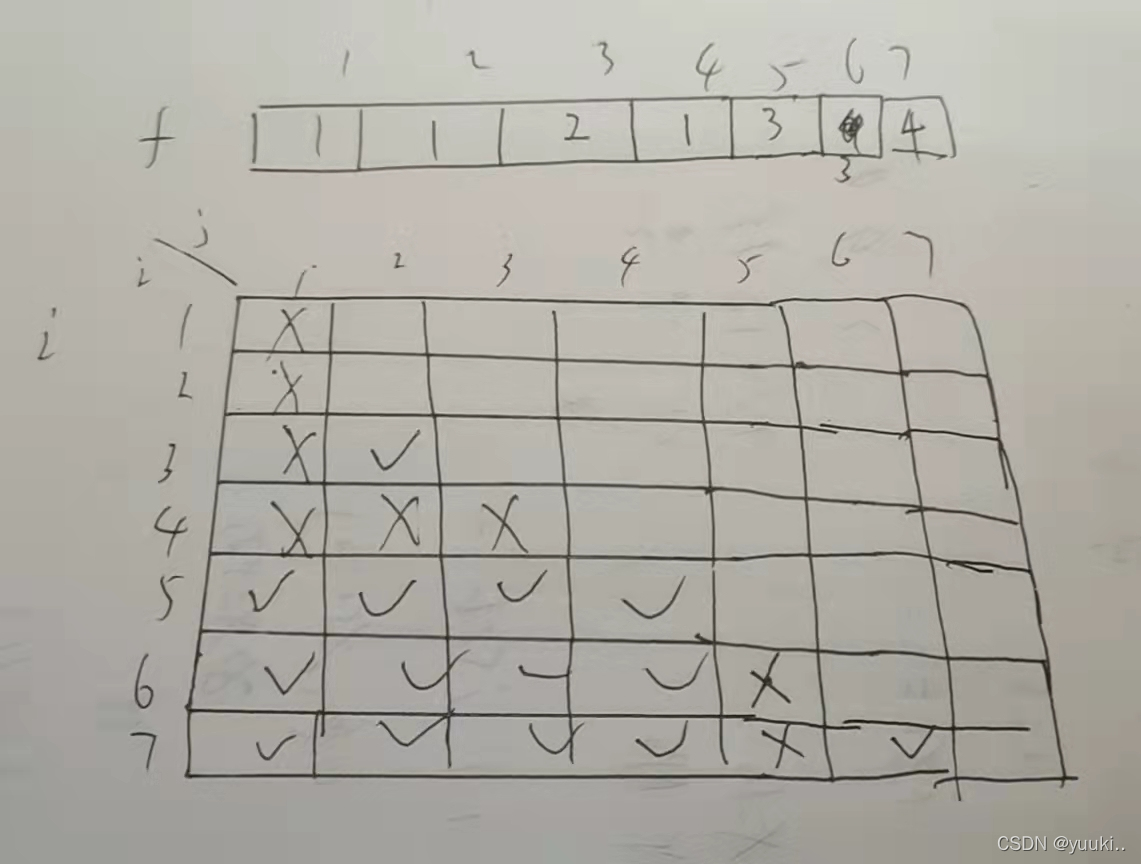
此图为f[ ]的状态表示和 i , j 的比较 

下面的代码是逆序输出储存最长子序列

#include<bits/stdc++.h>
using namespace std;
int a[10000];
int f[10000];
int g[10000];
int main()
{
    int n;
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>a[i];
    }
    for(int i=1;i<=n;i++)
    {
        f[i]=1;
        g[i]=0;
        for(int j=1;j<i;j++)
        {
            if(a[j]<a[i])
            {
                if(f[i]<f[j]+1)
                {
                    f[i]=f[j]+1;
                    g[i]=j;
                }
            }
        }
    }
    int k=1;
    for(int i=1;i<=n;i++)
    {
        if(f[k]<f[i])
        {
            k=i;
        }
    }
    cout<<f[k]<<endl;
    for(int i=0,len=f[k];i<len;i++)
    {
        cout<<a[k]<<" ";
        k=g[k];
    }
    return 0;
}

282 石子合并

 

#include<bits/stdc++.h>
using namespace std;
const int N=10000;
int s[N];
int f[N][N];
int n;
int main()
{
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>s[i];
    }
    for(int i=1;i<=n;i++) s[i]+=s[i-1];
    for(int len=2;len<=n;len++)
    {
        for(int i=1;i+len-1<=n;i++)
        {
            int l=i,r=i+len-1;
            f[l][r]=1e8;
            for(int k=l;k<r;k++)
            {
                f[l][r]=min(f[l][r],f[l][k]+f[k+1][r]+s[r]-s[l-1]);
            }
        }
    }
    cout<<f[1][n]<<endl;
}

338. 计数问题 - AcWing题库

# include <iostream>
# include <cmath>
using namespace std;

int dgt(int n) // 计算整数n有多少位
{
    int res = 0;
    while (n) ++ res, n /= 10;
    return res;
}

int cnt(int n, int i) // 计算从1到n的整数中数字i出现多少次 
{
    int res = 0, d = dgt(n);
    for (int j = 1; j <= d; ++ j) // 从右到左第j位上数字i出现多少次
    {
        // l和r是第j位左边和右边的整数 (视频中的abc和efg); dj是第j位的数字
        int p = pow(10, j - 1), l = n / p / 10, r = n % p, dj = n / p % 10;
        // 计算第j位左边的整数小于l (视频中xxx = 000 ~ abc - 1)的情况
        if (i) res += l * p; 
        if (!i && l) res += (l - 1) * p; // 如果i = 0, 左边高位不能全为0(视频中xxx = 001 ~ abc - 1)
        // 计算第j位左边的整数等于l (视频中xxx = abc)的情况
        if ( (dj > i) && (i || l) ) res += p;
        if ( (dj == i) && (i || l) ) res += r + 1;
    }
    return res;
}

int main()
{
    int a, b;
    while (cin >> a >> b , a)
    {
        if (a > b) swap(a, b);
        for (int i = 0; i <= 9; ++ i) cout << cnt(b, i) - cnt(a - 1, i) << ' ';
        cout << endl;
    }
    return 0;
}

作者：Alicia编程果果
链接：https://www.acwing.com/solution/content/7128/
来源：AcWing
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处。

291. 蒙德里安的梦想 - AcWing题库