PyTorch张量操作与自动求导基础-优快云博客

一、张量

是pytorch运算中的基本单元

阶	数学实例	python	例子
0	标量（数字）	大小	1
1	向量	大小和方向	[1,2]
2	矩阵	数据表	[[1,2],[3,4]]
3	3阶张量	数据立体（时间序列数据股价文本数据单张彩色图片(RGB)	[[[1,2],[3,4]],[[4,5],[3,6]]]
n	n阶

存储在各种类型张量的公用数据集类型：

3维 = 时间序列
4维 = 图像
5维 = 视频

参数：

torch.tensor(

data	张量阶	1，2，3
*	其他
dtype	数据类型	float、long，int8···
device
requires_grad	是否允许求导
pin_momemory	是否放到内存中

)

1、创建tensor：

（1）用dtype指定类型，注意类型匹配

import torch
a=torch.tensor(1.0,dtype=torch.float)
b=torch.tensor(1,dtype=torch.long)
c=torch.tensor(1.0,dtype=torch.int8)
print(a,b,c)

#结果
tensor(1.) tensor(1) tensor(1, dtype=torch.int8)

（2）使用指定类型函数随机初始化指定tensor大小

d=torch.FloatTensor(2,3)#2行3列浮点数矩阵
e=torch.IntTensor(3)#随机3个整形整数
f=torch.IntTensor([1,2,3,4])#转换可识别数列
print(d,'\n',e,'\n',f)

tensor([[0., 0., 0.],
        [0., 0., 0.]]) 
 tensor([1, 0, 0], dtype=torch.int32) 
 tensor([1, 2, 3, 4], dtype=torch.int32)

（3）tensor和numpy array之间相互转换

g=np.array([[1,2,3],[4,5,6]])
h=torch.tensor(g)#基本不变
i=torch.from_numpy(g)
j=h.numpy()#tensor更改为numpy变换指令
print(h,'\n',i,'\n',j)

tensor([[1, 2, 3],
        [4, 5, 6]], dtype=torch.int32) 
 tensor([[1, 2, 3],
        [4, 5, 6]], dtype=torch.int32) 
 [[1 2 3]
 [4 5 6]]

2、常见构造tensor的函数

常见tensor函数	功能
torch.rand/randn(n,m)	随机n行m列矩阵，rand是[0,1)均匀分布；randn是服从N(0，1)的正态分布
torch.one(n,m)	全1矩阵
torch.zeros(n,m)	全0矩阵
torch.eye()	对角为1，其余为0
torch.arange(s,e,step)	从s到e，步长为step
torch.linspace(s,e,steps)	从s到e，均匀分成step份
torch.normal(mean,std)	正态分布(均值为mean，标准差是std)
torch.randperm(m)	随机排列

k=torch.rand(2,3)
l=torch.ones(2,3)
m=torch.zeros(2,3)
n=torch.arange(0,10,2)
print(k,'\n',l,'\n',m,'\n',n)

tensor([[0.4664, 0.3565, 0.6780],
        [0.7851, 0.5919, 0.6786]]) 
 tensor([[1., 1., 1.],
        [1., 1., 1.]]) 
 tensor([[0., 0., 0.],
        [0., 0., 0.]]) 
 tensor([0, 2, 4, 6, 8])

3、查看tensor的维度

k.shape()
k.size()

4、tensor的运算

（1）加法操作

o=torch.add(k,l)
tensor([[1.3597, 1.7565, 1.1835],
        [1.9602, 1.1388, 1.7656]])

（2）索引操作

print(o[:,1])#:表所有行，1表第一列（从0开始数）

tensor([1.7565, 1.1388])

（3）维度变换

print(o.view((3,2)))#3行2列
print(o.view(-1,2))#-1---自动填补

tensor([[1.3597, 1.7565],
        [1.1835, 1.9602],
        [1.1388, 1.7656]])
        
tensor([[1.3597, 1.7565],
        [1.1835, 1.9602],
        [1.1388, 1.7656]])

5、tensor的广播机制

当对两个形状不同的 Tensor 按元素运算时，可能会触发广播(broadcasting)机制：先适当复制元素使这两个 Tensor 形状相同后再按元素运算-----自动将格式配齐---取最大维数

p=torch.arange(1,3).view(1,2)
q=torch.arange(1,4).view(3,1)
print(p,'\n',q,'\n',p+q)

tensor([[1, 2]]) 
 tensor([[1],
        [2],
        [3]]) 
 tensor([[2, 3],
        [3, 4],
        [4, 5]])

6、扩展&压缩tensor的维度：squeeze

o=torch.add(k,l)
r=o.unsqueeze(1)
print(o,'\n',r,'\n',r.shape)

tensor([[1.6903, 1.6787, 1.3914],
        [1.9450, 1.1150, 1.4855]]) 
 tensor([[[1.6903, 1.6787, 1.3914]],

        [[1.9450, 1.1150, 1.4855]]]) #强行增加了一行
 torch.Size([2, 1, 3])

某维维度为1可以进行squeeze

二、自动求导

将优化目标的损失降到最小，进行迭代求导的过程

1、pytorch实现训练模型：

-输入数据，正向传播
-同时创建计算图
-计算损失函数
-损失函数反向传播
-更新模型参数

tensor数据结构是实现自动求导的基础

PyTorch自动求导提供了计算雅可比乘积的工具

损失函数l对输出y的导数为：

$v=\left ( \frac{\partial l}{\partial y_{1}} \cdot \cdot \cdot\frac{\partial l}{\partial y_{m}}\right )$

那么l对输入x的倒数：

$vJ=(\frac{\partial l}{\partial y}~\cdots ~\frac{\partial l}{\partial y_{m}})\begin{pmatrix} \frac{\partial y_{1}}{\partial x_{1}} &\cdots &\frac{\partial y_{1}}{\partial x_{n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial y_{m}}{\partial x_{1}} &\cdots & \frac{\partial y_{m}}{\partial x_{n}} \end{pmatrix}=(\frac{\partial l}{\partial x_{1}}\cdots \frac{\partial l}{\partial x_{n}})$

多元函数求导的雅可比矩阵：

$J=\begin{pmatrix} \frac{\partial y_{1}}{\partial x_{1}} & \cdots &\frac{\partial y_{1}}{\partial x_{n}} \\ \vdots & \ddots &\vdots \\ \frac{\partial y_{m}}{\partial x_{1}} & \cdots &\frac{\partial y_{m}}{\partial x_{n}} \end{pmatrix}$

复合函数求导的链式法则：

若 $h(x)=f(g(x))$ ，则 $h{}'(x)=f{}'(g(x))\cdot g{}'(x)$

2、动态计算图（DCG）

---张量和运算结合起来创建动态计算图

静态图和动态图

静态图---定义计算与数值

动态图---定义数值即可，然后用图的形式串联

3、示例：

import torch
x1=torch.tensor(1.0,requires_grad=True)
x2=torch.tensor(2.0,requires_grad=True)
y=x1+2*x2
print(y)

tensor(5., grad_fn=<AddBackward0>)

前向传播没有导数存在，没有梯度。反向传播看导数大小---导数会累积，重复运行相同命令，grad会增加

（每次计算前需要清除当前导数值避免累计，可通过pytorch的optimizer实现）

y=x1+2*x2
y.backward()#调用 .backward()自动计算所有的梯度
print(x1.grad.data)
print(x2.grad.data)#这个张量的所有梯度将会自动累加到.grad属性。
print(y)

tensor(1.)
tensor(2.)
tensor(5., grad_fn=<AddBackward0>)#y是计算的结果，所以它有grad_fn属性。

.detach()方法阻止一个张量被跟踪历史，将其与计算历史分离，并阻止它未来的计算记录被跟踪、也可通过将代码块包装在with torch.no_grad(): 中，来阻止 autograd 跟踪设置了.requires_grad=True的张量的历史记录。

x = torch.randn(3, requires_grad=True)
print(x.requires_grad)
print((x ** 2).requires_grad)

with torch.no_grad():
    print((x ** 2).requires_grad)

True
True
False

想要修改 tensor 的数值，但是又不希望被 autograd 记录(即不会影响反向传播)，那么我们可以对 tensor.data 进行操作。

x = torch.ones(1,requires_grad=True)

print(x.data) # 还是一个tensor
print(x.data.requires_grad) # 但是已经是独立于计算图之外

y = 2 * x
x.data *= 100 # 只改变了值，不会记录在计算图，所以不会影响梯度传播

y.backward()
print(x) # 更改data的值也会影响tensor的值 
print(x.grad)

tensor([1.])
False
tensor([100.], requires_grad=True)
tensor([2.])

三、并行计算

1、减少显存占用

2、计算速度快

3、提升训练效果

1、cuda

CUDA是NVIDIA提供的GPU并行计算框架。

在PyTorch使用 CUDA表示当我们使用了 .cuda() 时，我们的模型或者数据从CPU迁移到GPU(0)当中，通过GPU开始计算。

2、并行方法：

方法
Network Partitioning	网络结构分布到不同设备中
Layer-wise Partitionong	同一层的任务分布到不同数据中
Data Parallelism	不同数据分布到不同设备中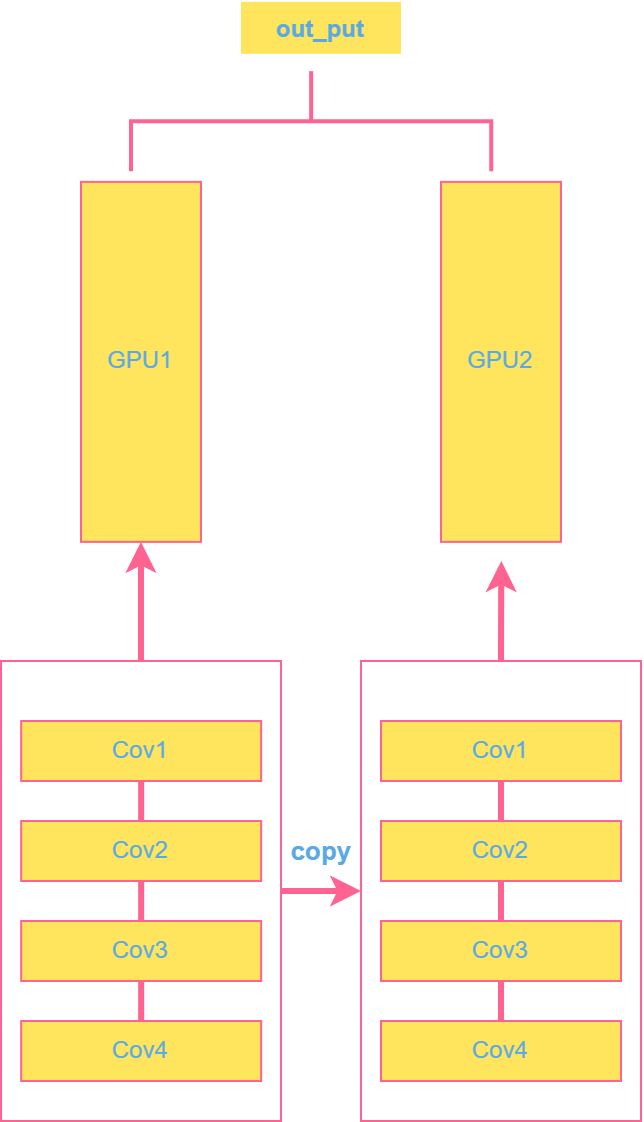

3、cuDNN与CUDA

cuDNN是用于深度神经网络的加速库
cuDNN基于CUDA完成深度学习的加速