排序二叉树的插入、删除操作

干嘛˂᷅

于 2022-07-17 21:46:09 发布

阅读量329

点赞数

分类专栏：数据结构文章标签： c++ 数据结构算法排序算法

本文链接：https://blog.youkuaiyun.com/qq_52363737/article/details/125829203

版权

数据结构专栏收录该内容

1 篇文章

订阅专栏

排序二叉树的定义：即任一根节点的值，大于其左子树的任意值，且小于其右子树的任意值，并且，通过中序遍历排序二叉树，我们可以得到一个已经排好序的升序序列。

排序二叉树的定义以及构建

定义二叉排序树

typedef struct {
    int value;
}ElemType;

typedef struct BSTree{
    ElemType data;
    BSTree *lChild, *rChild;
}BSTree, *BSTreeNode;

构建二叉排序树

构建二叉排序树的过程很简单，我们只需遵从二叉树的定义：即小于根节点的值全都位于根节点的左子树，大于根节点的值全部位于根节点的右子树，并且这是一个递归的的定义，故我们采用递归来完成排序二叉树的构建。该算法也是排序算法的一种

void initBSTree(BSTreeNode &tree, int data[], int length){
// 遍历所有元素，以此的将每一个元素插入到排序二叉树中
    for (int i = 0; i < length; ++i){
        insertNode(tree, data[i]);
    }
}
void insertNode(BSTreeNode &treeNode, int value){
    // 如果当前传入的根节点为null,那么我们直接新建一个节点并且完成赋值
    if (treeNode == nullptr){
        treeNode = new BSTree;
        treeNode->data.value = value;
        treeNode->lChild = nullptr, treeNode->rChild = nullptr;
    }
    
    // 如果传入的值小于节点的值，那么调用自身，并且传入树的左子树   
    else if (value < treeNode->data.value) insertNode(treeNode->lChild, value);
    // 否则调动自身，传入树的右子树
    else insertNode(treeNode->rChild, value);
}

不太熟悉C++语法的朋友可能不清楚上面代码的new是什么意思，其实这里的new跟C语言的malloc是一个意思，都是在内存开辟一块空间，并且返回该地址的指针，但是有一点需要注意的是，通过new开辟的空间，释放时需要使用delete关键字，而通过malloc关键字开辟的空间，需要使用free来释放，故上述代码的new BSTree亦可以替换为：
treeNode = (BSTree *)malloc(sizeof(BSTree))

测试构建

我们传入这么一组数据
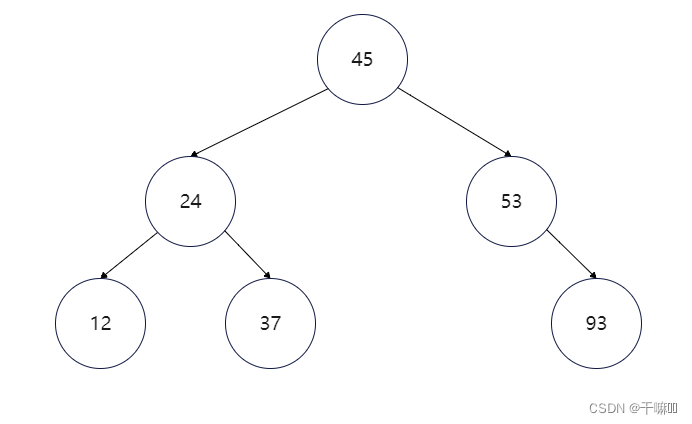
int arr[] = {45, 24, 53, 12, 37, 93};
该数据的排序二叉树如下图所示

中序遍历的结果
void mediumOrderTraverse(BSTreeNode &treeNode){
    if (treeNode == nullptr) return;
    else{
        mediumOrderTraverse(treeNode->lChild);
        cout << treeNode->data.value << " ";
        mediumOrderTraverse(treeNode->rChild);
    }
}
输出了一个有序序列，可见，我们完成了二叉排序树的构建

删除排序二叉树

比起插入节点，删除节点看起来要麻烦的多，删除节点有个最基本的要求，就是在删除了某节点后，依旧能保持排序二叉树的特性。删除节点一般有三种情况

情况1：

待删除节点是一个叶子节点，我们直接将其删除即可，这是最简单的一种情况

情况2：

待删除节点是一个非叶子结点，且该节点必然只有一个子节点，即要么左子树为空，要么右子树为空

情况3：

也就是最麻烦的情况，左右子树均不为空

下面的代码中，我们以此来讨论三种不同情况的删除

我们分开讨论（下面有全部可执行代码）

先获取待删除节点

BSTree *ptr = treeNode, *current, *q, *temp;
// 查找待删除的元素
while (ptr){
    if (ptr->data.value == key) break;
    current = ptr;
    if(ptr->data.value > key) ptr = ptr->lChild;
    lse ptr = ptr->rChild;
}

如果查找失败，直接返回，什么都不做

    if (ptr == nullptr) return;

第一种删除情况和第二种删除情况是可以同时处理

    // 左子树为空的情况
    if (ptr->lChild == nullptr){
        // 判断删除节点位于父节点的左边还是右边，下同
        if (current->lChild == ptr) current->lChild = ptr->rChild;
        else current->rChild = ptr->rChild;
        free(ptr);
    }
    // 右子树为空的情况
    else if (ptr->rChild == nullptr){
        cout << "右空" << endl;
        if (current->rChild == ptr) current->rChild = ptr->lChild;
        else current->lChild = ptr->lChild;;
        free(ptr);
    }

第三种删除情况（待删除节点同时拥有左子树和右子树）

        // 找到直接前驱赋值给temp, 且将其父节点赋值给 q
        temp = ptr->lChild;
        q = ptr;
        while (temp->rChild){
            q = temp;
            temp = temp->rChild;
        }
        // 用直接前驱替换待删除节点，随后删除直接前驱
        ptr->data = temp->data;
        // 重连待删除节点的右子树
        if (q != ptr) q->rChild = temp->lChild;
        // 重连左节点
        else q->lChild = temp->lChild;
        cout << "直接前驱是 -> " << temp->data.value << endl;
        // 删除直接前驱
        free(temp);

        上面的第三种情况的代码可能不好理解的在if判断那里，为什么说 q ≠ ptr 就令q的右节点等于直接前驱的左节点？

        首先有一点需要知道的是，无论是给 q的左子树还是右子树赋值，赋的值是一定不会变的，因为待删除节点的直接前驱一定不会存在右子树，当然这是放在我们目前需要删除的情况下来讨论的，不然直接前驱就是他的右子树

        理解了上面的那段文字的话下面就好理解了，因为q是随着temp的迭代而实时更新的，如果说 q ≠ ptr(找到到的需要删除的节点)，那么就说明，temp至少迭代了一次，且待删除节点的左子树不是直接前驱，此时我们需要将找到的直接前驱的父节点的右子树等于直接前驱的左子树（上面讨论过，直接前驱不存在右子树），这样子才不会丢失直接前驱节点的后继结点信息。

        如果待删除节点的左子树就是直接前驱，那么就可以直接令待删除节点的左子树的值为其直接前驱的左子树即可。

删除节点测试

还是使用上面数据

    int arr[] = {45, 12, 3, 1,  37, 24, 53, 100, 61, 90, 78};
    initBSTree(treeNode, arr, sizeof(arr) / sizeof(arr[0]));
    deleteNode(treeNode, 12);
    deleteNode(treeNode, 1);
    deleteNode(treeNode, 45);
    deleteNode(treeNode, 61);

依次删除四个节点，覆盖了所有可能的情况

结果如下

全部可运行代码

//
// Created by Sakura on 2022-07-16.
//
#include "iostream"
#include "malloc.h"
using namespace std;

typedef struct {
    int value;
} ElemType;

typedef struct BSTree {
    ElemType data;
    BSTree *lChild, *rChild;
} BSTree, *BSTreeNode;

void initBSTree(BSTreeNode &tree, int[], int);

void insertNode(BSTreeNode &, int);

void mediumOrderTraverse(BSTreeNode &);

void deleteNode(BSTreeNode &, int);

int main() {
    system("chcp 65001 > nul");
    BSTreeNode treeNode = nullptr;
//    int arr[] = {45, 24, 53, 12, 37, 93, 98};
    int arr[] = {45, 12, 3, 1,  37, 24, 53, 100, 61, 90, 78};
    initBSTree(treeNode, arr, sizeof(arr) / sizeof(arr[0]));
    deleteNode(treeNode, 12);
    deleteNode(treeNode, 1);
    deleteNode(treeNode, 45);
    deleteNode(treeNode, 61);
    cout << "[ ";
    mediumOrderTraverse(treeNode);
    cout << "]" << endl;
}

void initBSTree(BSTreeNode &tree, int data[], int length) {
    for (int i = 0; i < length; ++i) {
        insertNode(tree, data[i]);
    }
}

void insertNode(BSTreeNode &treeNode, int value) {
    if (treeNode == nullptr) {
        treeNode =  (BSTree *) malloc(sizeof(BSTree));
        treeNode->data.value = value;
        treeNode->lChild = nullptr, treeNode->rChild = nullptr;
    } else if (value < treeNode->data.value) insertNode(treeNode->lChild, value);
    else insertNode(treeNode->rChild, value);
}

/**
 *
 * @param treeNode
 */
void mediumOrderTraverse(BSTreeNode &treeNode) {
    if (treeNode == nullptr) return;
    else {
        mediumOrderTraverse(treeNode->lChild);
        cout << treeNode->data.value << " ";
        mediumOrderTraverse(treeNode->rChild);
    }
}

void deleteNode(BSTreeNode &treeNode, int key) {
    BSTree *ptr = treeNode, *current, *q, *temp;
    // 查找待删除的元素
    while (ptr){
        if (ptr->data.value == key) break;
        current = ptr;
        if(ptr->data.value > key) ptr = ptr->lChild;
        else ptr = ptr->rChild;
    }
    if (ptr == nullptr) return;
    // 左子树为空的情况
    if (ptr->lChild == nullptr){
        if (current->lChild == ptr) current->lChild = ptr->rChild;
        else current->rChild = ptr->rChild;
        free(ptr);
    }
    else{
        // 找到直接前驱赋值给temp, 且将其父节点赋值给 q
        temp = ptr->lChild;
        q = ptr;
        while (temp->rChild){
            q = temp;
            temp = temp->rChild;
        }
        // 用直接前驱替换待删除节点，随后删除直接前驱
        ptr->data = temp->data;
        // 重连待删除节点的右子树
        if (q != ptr) q->rChild = temp->lChild;
        // 重连左节点
        else q->lChild = temp->lChild;
        // 删除直接前驱
        free(temp);
    }


}

细心的童鞋可能发现了，在完整的代码中，我并没有将右子树为空的情况列入，但是代码依旧可以正常执行，这是为什么~~ 还请童鞋自己代入分析一下吧~