备考软件设计师下午题第四题

解01背包问题

 核心算法：

不选第 i 个物品： f [ i ] [ j ] = f [ i - 1 ] [ j ]

选第 i 个物品：f [ i ] [ j ] = v [ i ] + f [ i - 1 ] [ j - w [ i ] ]

求最优解： f [ i ] [ j ] = max( f [ i - 1] [ j ] , f [ i - 1 ] [ j - w [ i ] + v [ i ] ] )

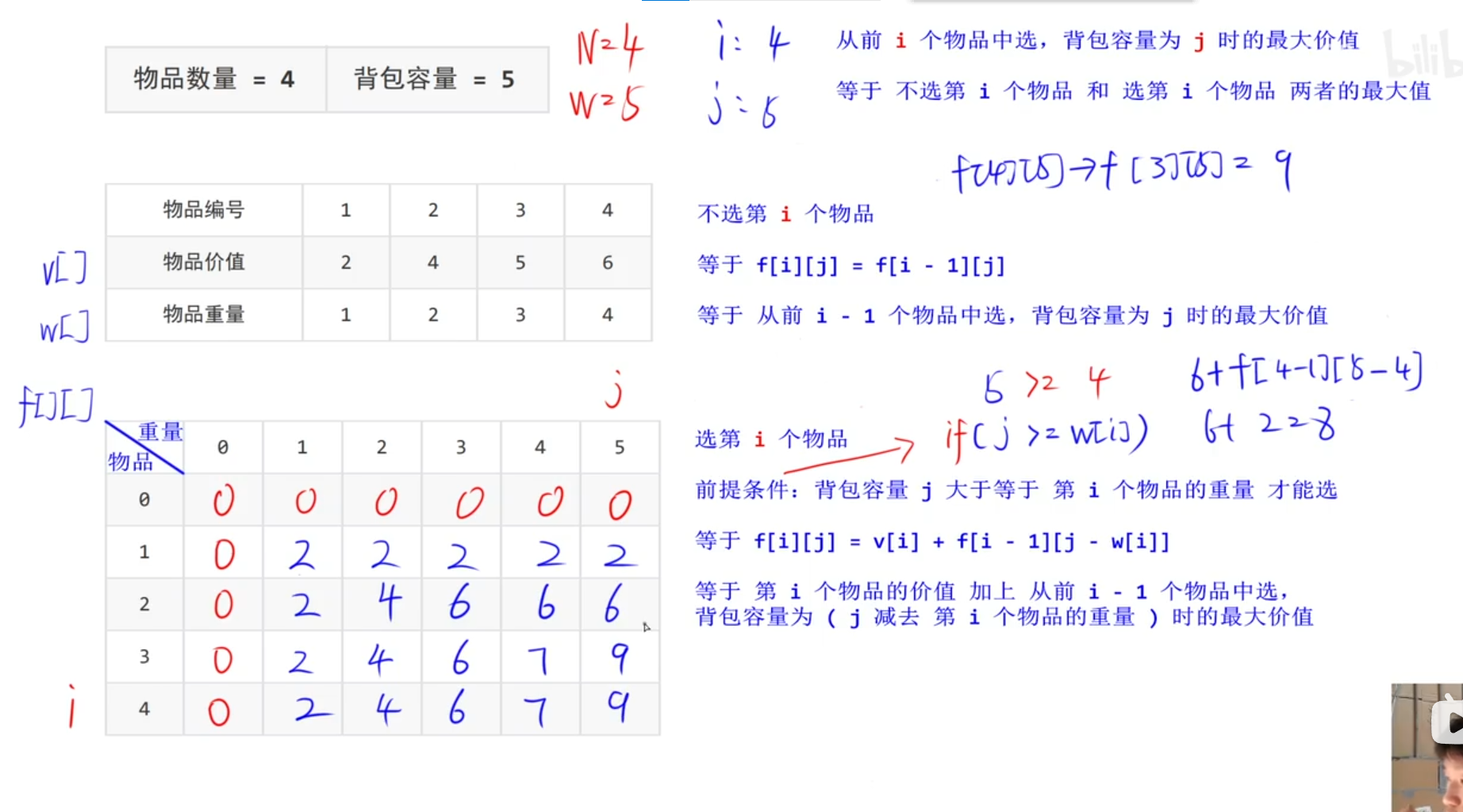
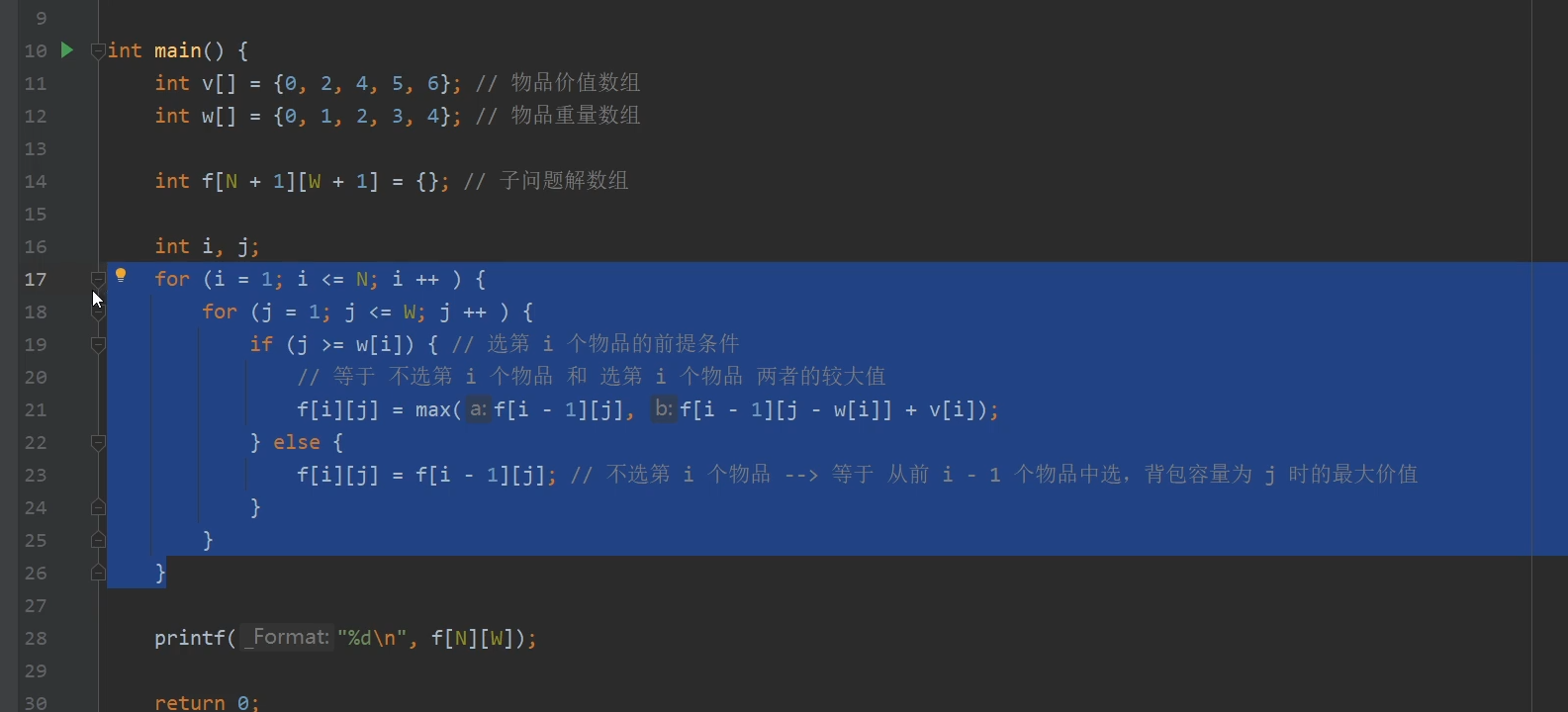
0-1背包问题的空间/时间复杂度

矩阵连乘问题的时间复杂度： O（n的3次方）

空间复杂度： O（n的平方）

动态规划

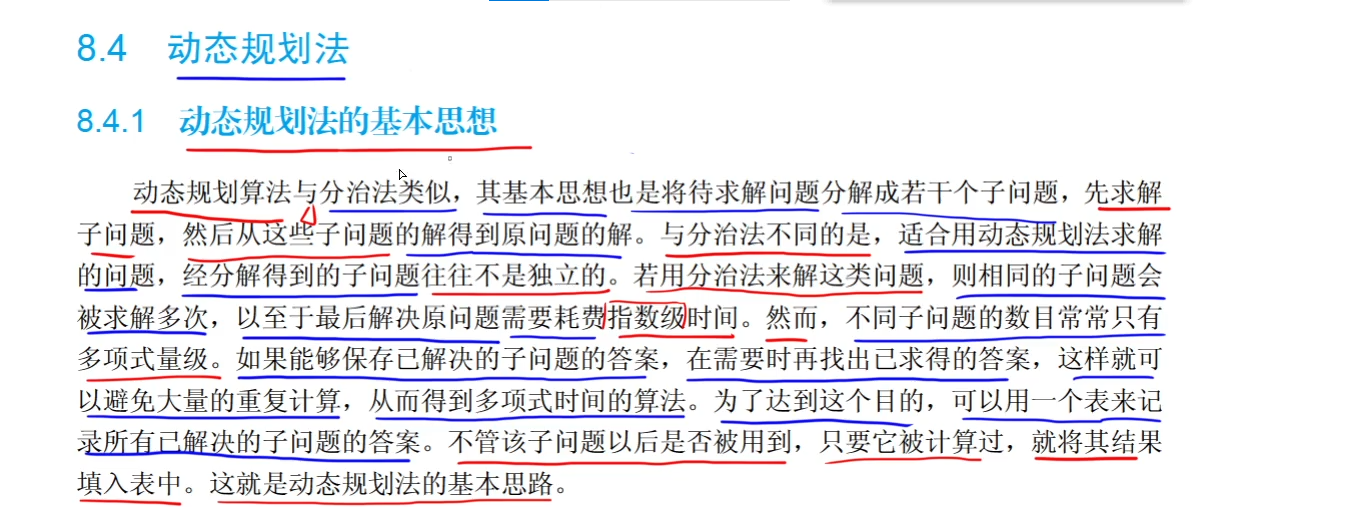
动态规划与分治法类似

相同：都是先将一个问题分成若干个子问题

不同：分治法是一个一个独立的去解决（可能导致运算成本过大）

动态规划是将一个子问题的解记录在一个表中，当其余子问题中有合适的解就直接代入，减少运算成本

动态规划通常用于解最优性质的问题

通常的步骤：

1.找出最优解的性质，并刻画其结构特征

2.递归地定义最优解的值

3.以自底向上的方式计算出最优值

4.根据计算最优值时得到的信息，构造一个最优解

只需要算出最优值：步骤1-3，要最优解：1-4

动态规划的两个性质：最优子结构、重叠子问题

分治法

递归的基本要素：边界条件、递归模式

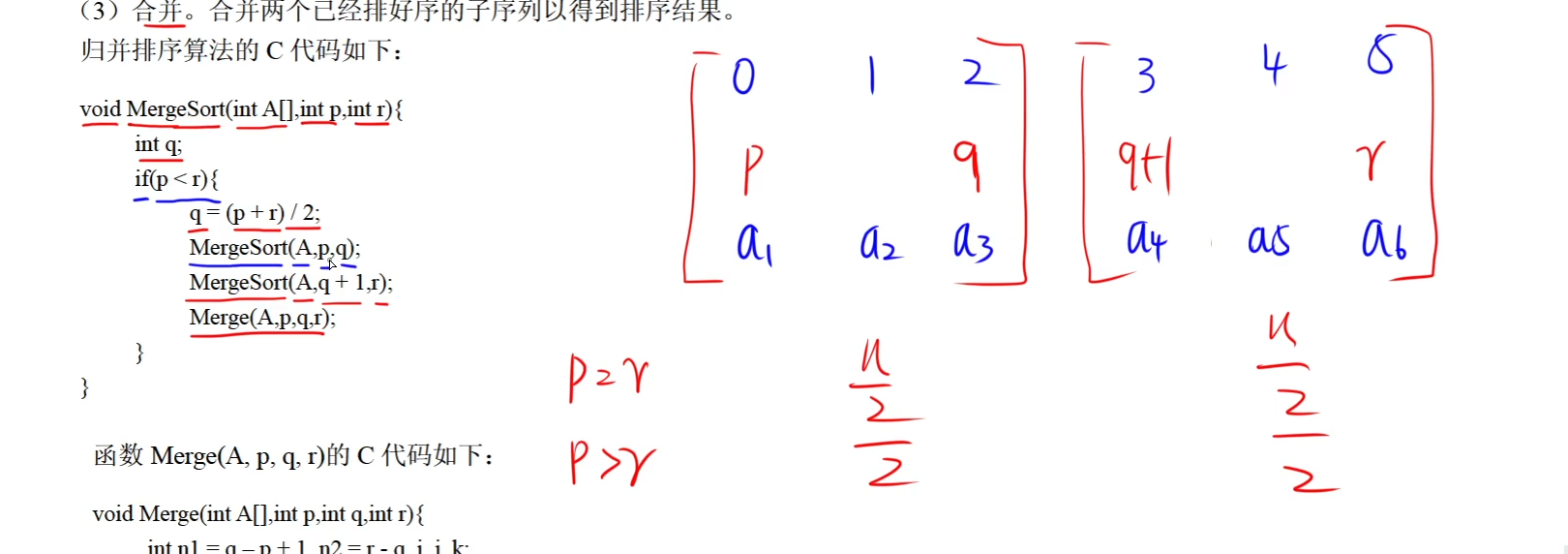
分治算法在每一层递归都有3个步骤：分解、求解、合并

空间复杂度为O（n）

时间复杂度：O(nlogn)

分解算法：

归并算法：

递归解N皇后问题

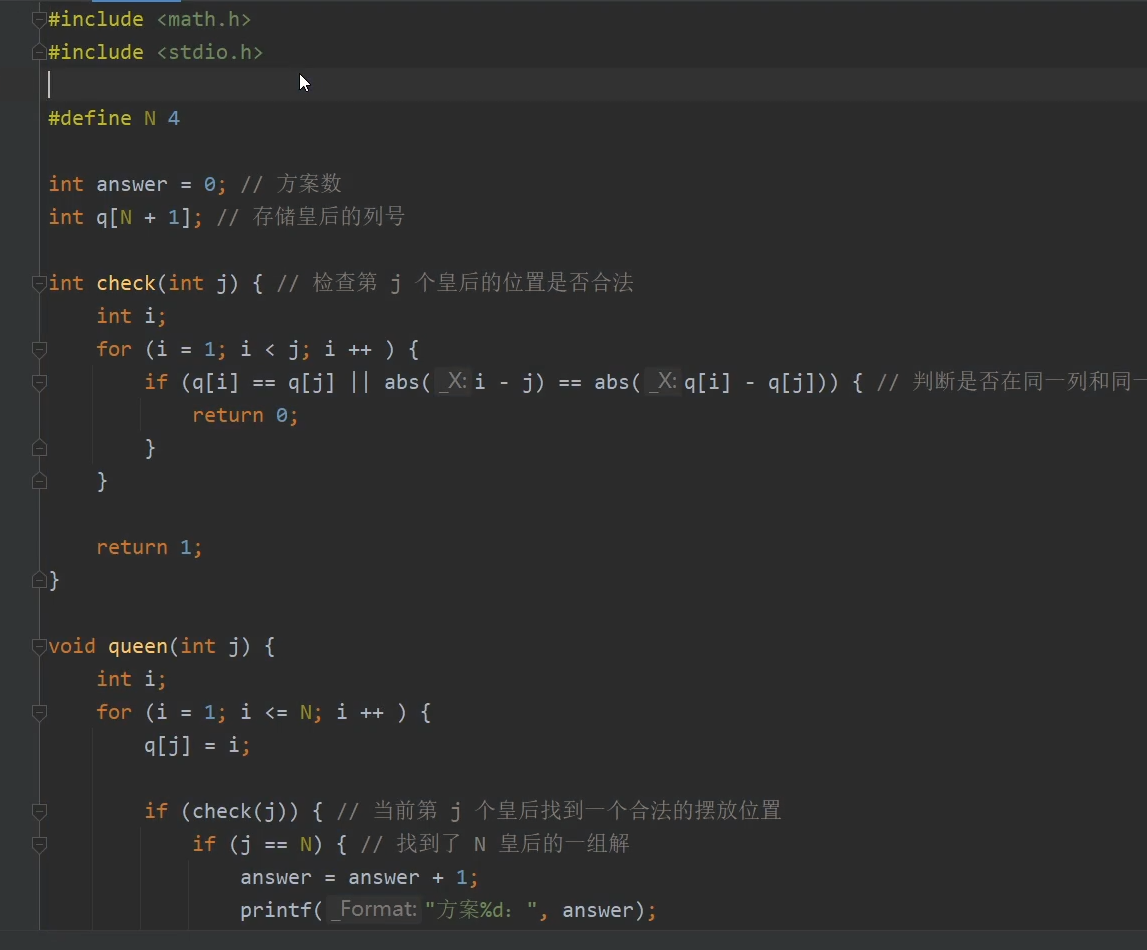
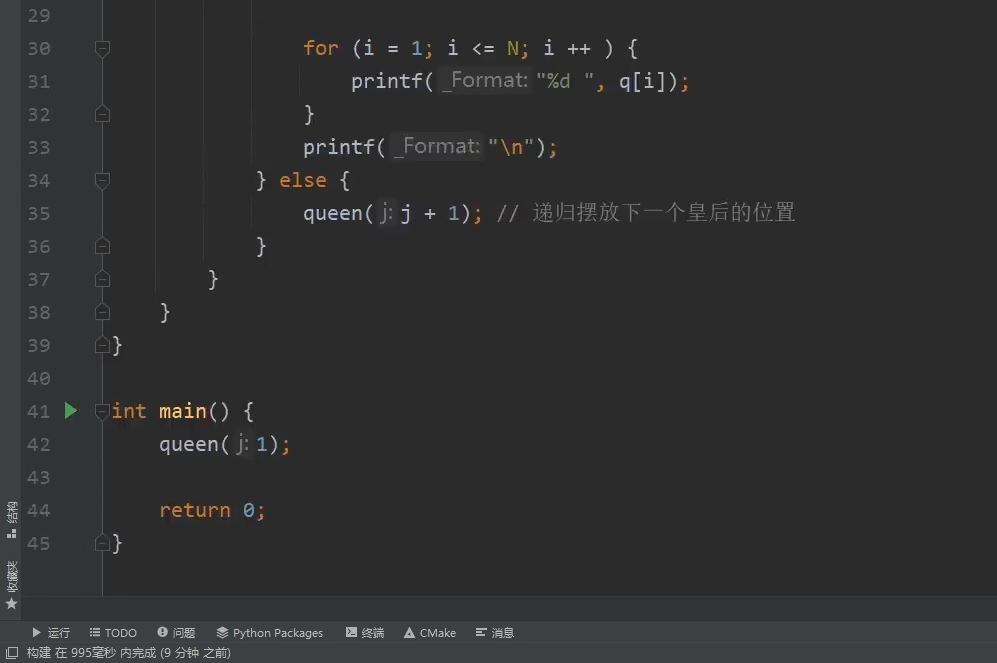
非递归解N皇后问题

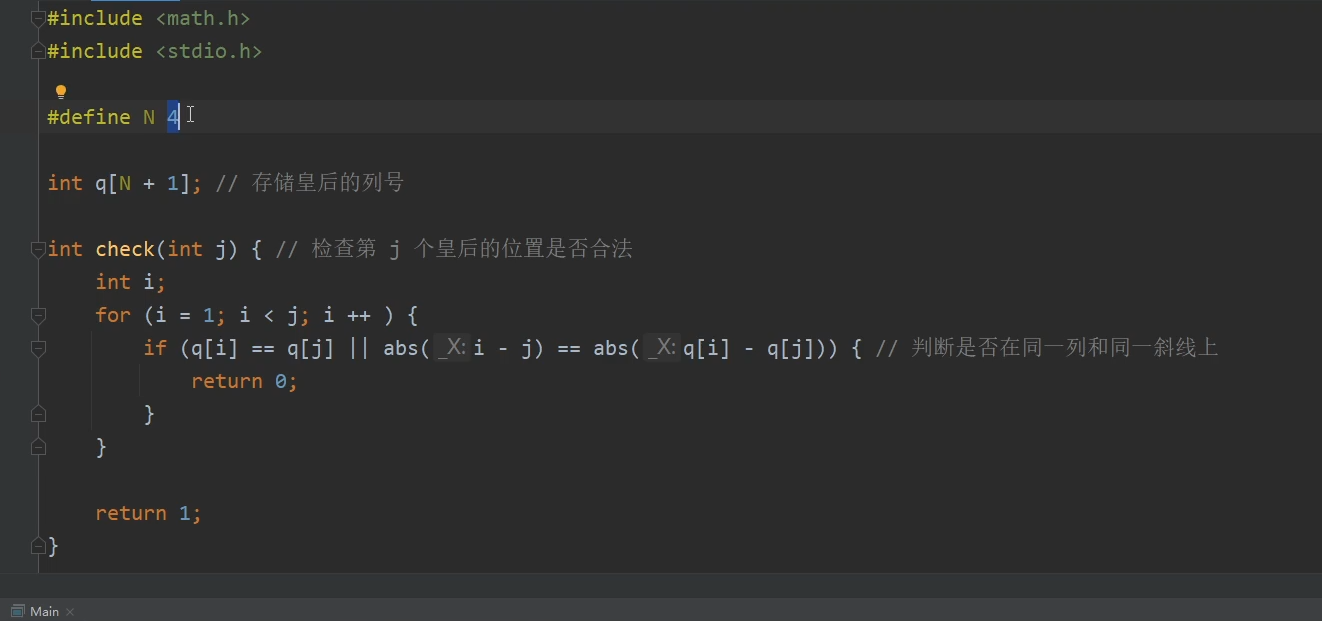
define是常量，n是变量名

printf是打印

q[3] = 4：表示第3个皇后在第3行的第4列

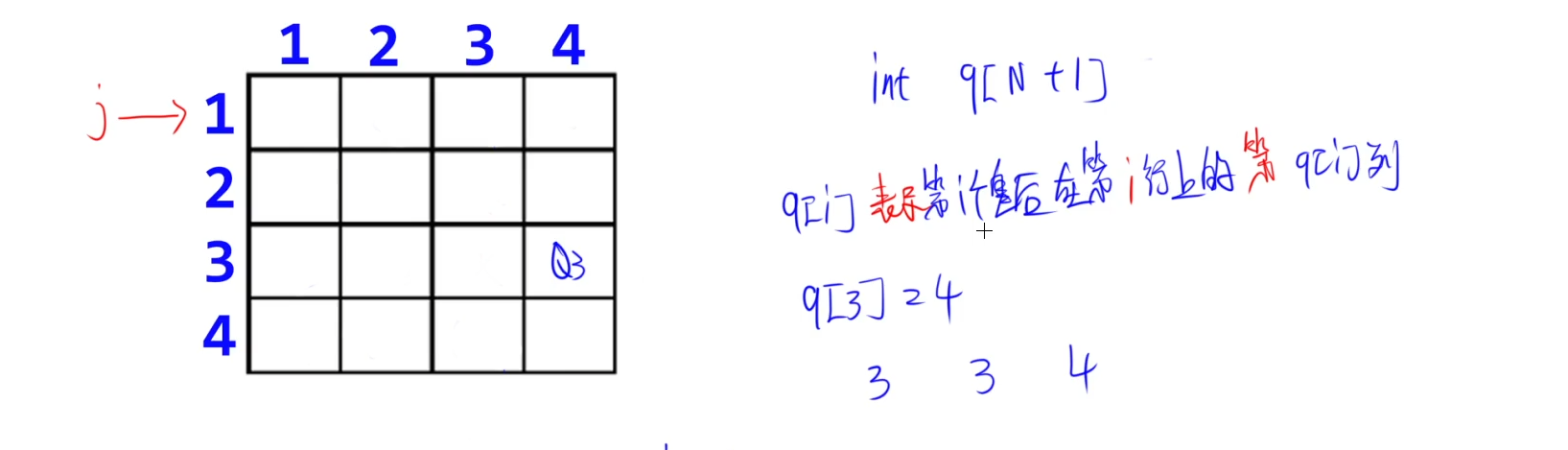
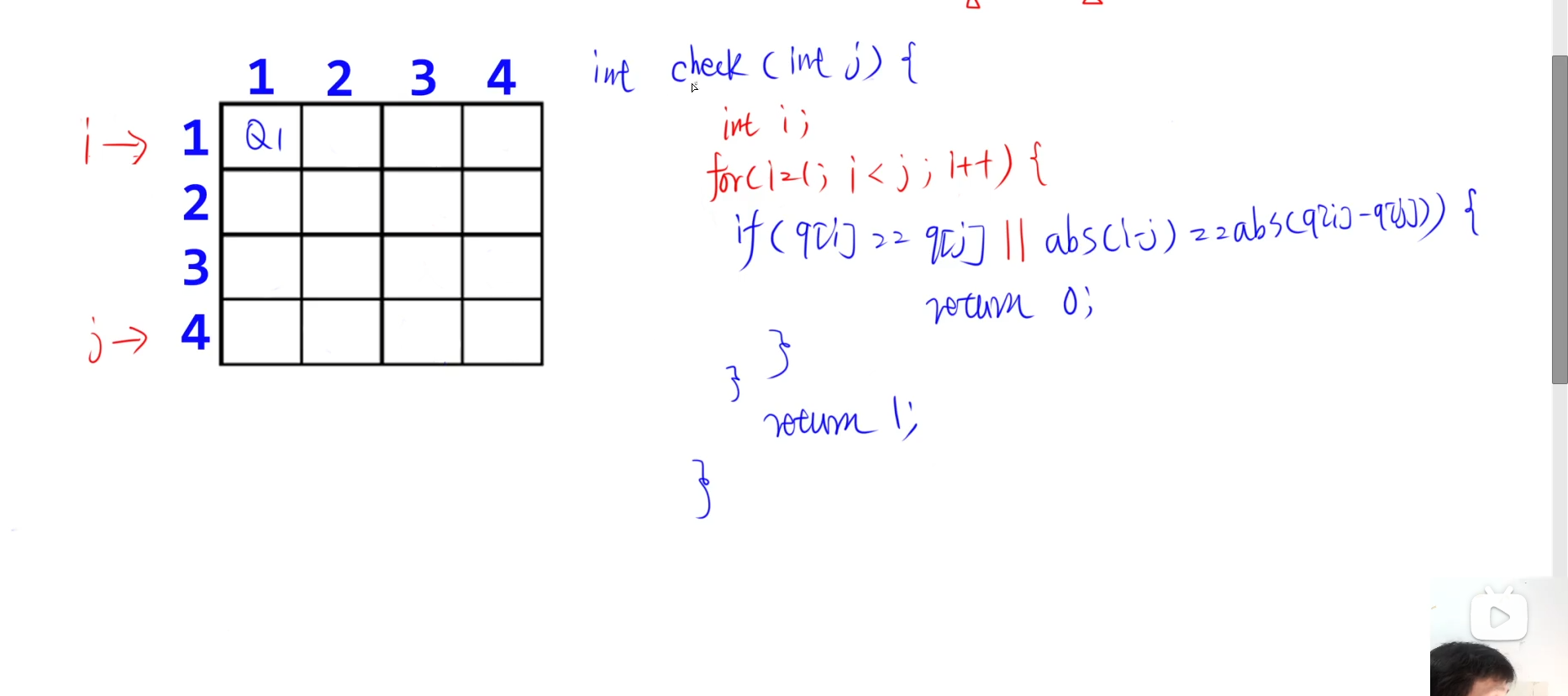
每放一个皇后：判断是否在同一列

行与行（相减）的绝对值 = 列与列（相减）的绝对值 是否相同

如果有一个相同则返回0（F，假）【位置不合法】

否则为1（T，真）

判断同一列：Qi列 == Qj列

判断同一条线：| Qi行 - Qj行 | == | Qi列 - Qj列 |

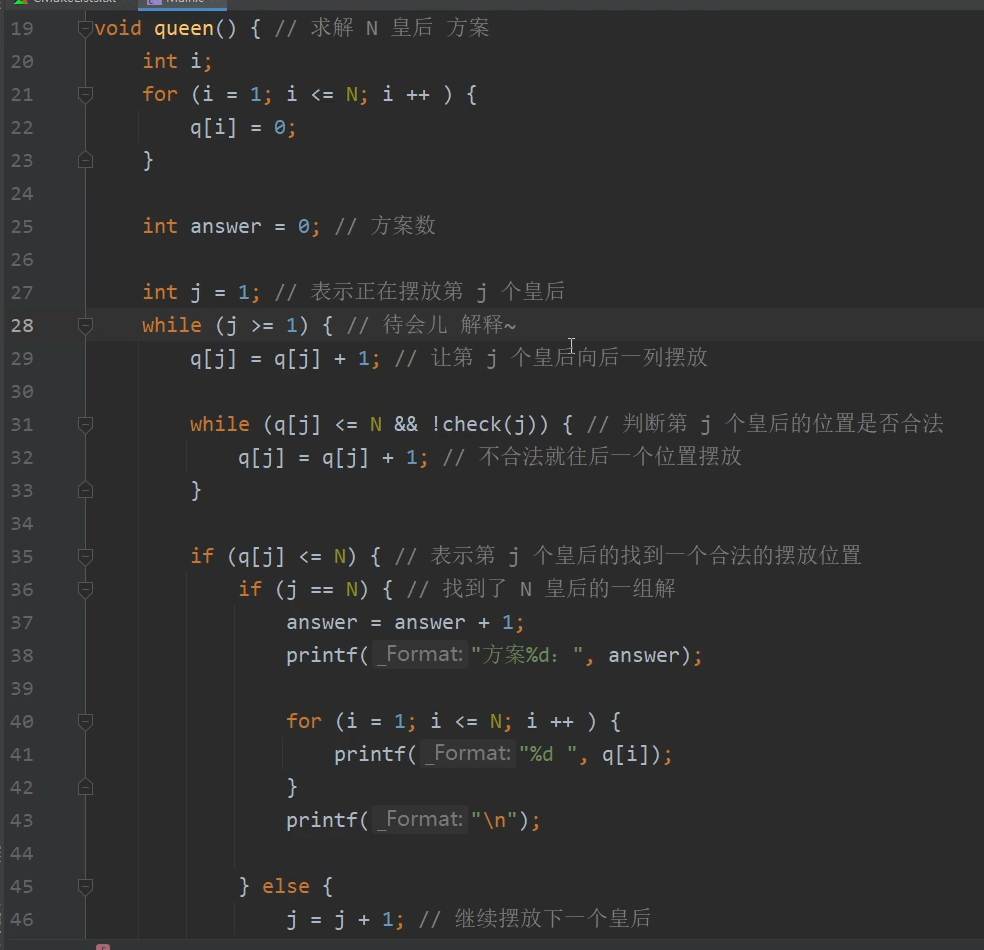
摆放第一个皇后时（j = 1）, 放在第一行（ q[j] = q[j] +1 ）

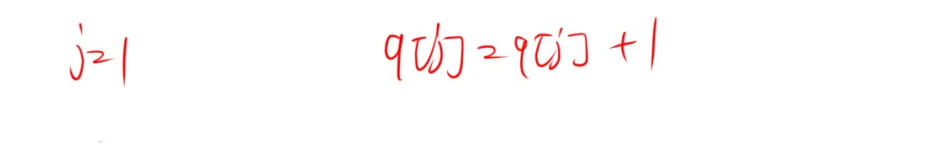
check(j) ：判断皇后位置是否合法的方法

不合法的时候往后面一行放

q[j]<=N：判断是否在棋盘之内

check(j) ：判断皇后位置是否合法的方法

如果有一个不对，那么

找到/没找到合法的一组解

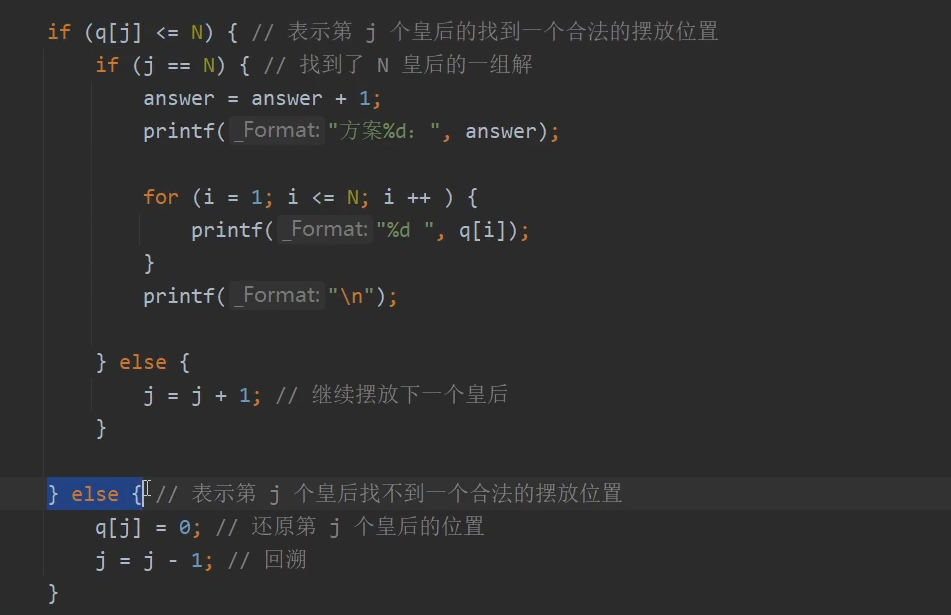
以下是案例：

N皇后问题

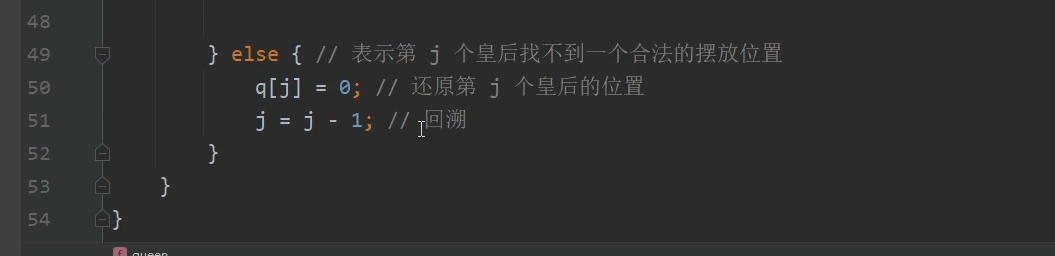
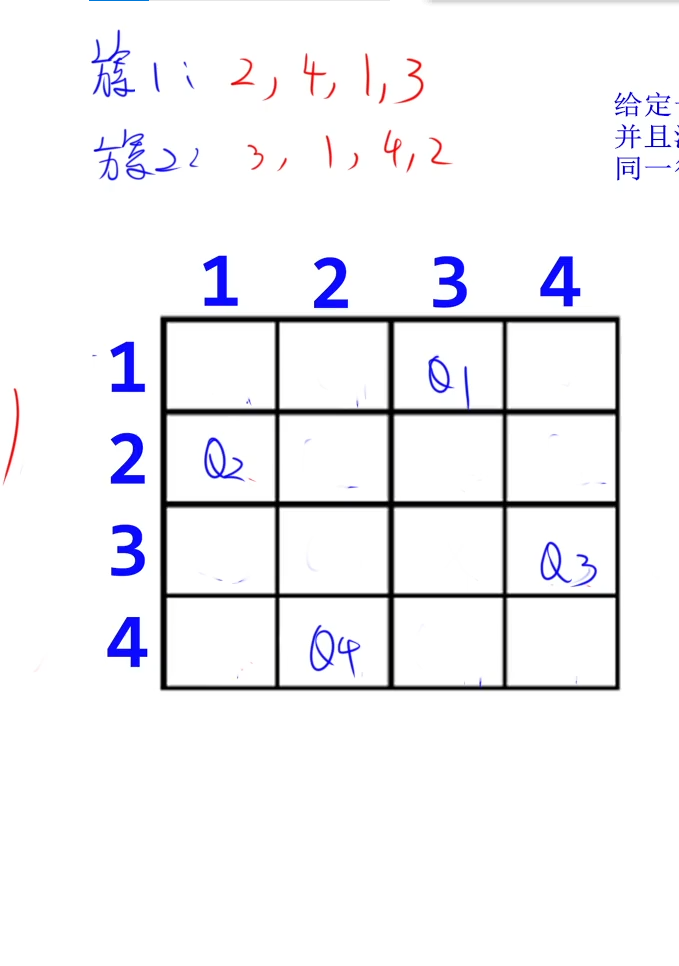
按行摆放皇后

行与行（相减）的绝对值 = 列与列（相减）的绝对值

方案1的答案反过来 = 方案2

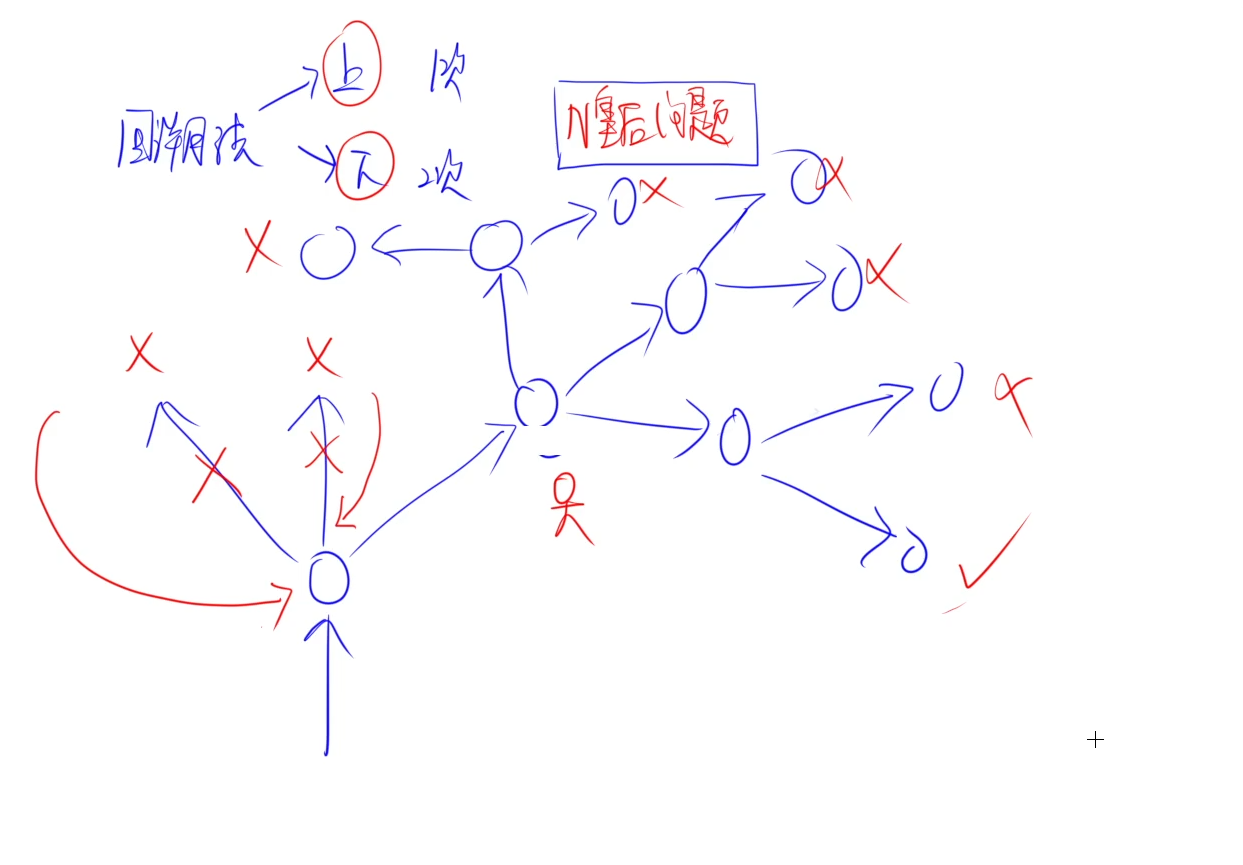
回溯法

回溯过程：一条路行不通，回到原点

该文章为笔记，教程为b站的zst_2001老师
zst_2001老师主页：https://space.bilibili.com/91286799?spm_id_from=333.999.0.0