关于代码优化的一个问题

CMU15-213中，有这样一个问题

在写C程序或是做算法题时，常常会忽略一个细节。

例如下面一段代码

void lower_quadratic(char *s) {
  size_t i;
  for (i = 0; i < strlen(s); i++)
    if (s[i] >= 'A' && s[i] <= 'Z')
      s[i] += 'a' - 'A';
}

乍看之下，并没有什么不妥当的地方，但是如果我们将字符串的长度放大到千或万或者更大级别，就会出现问题。

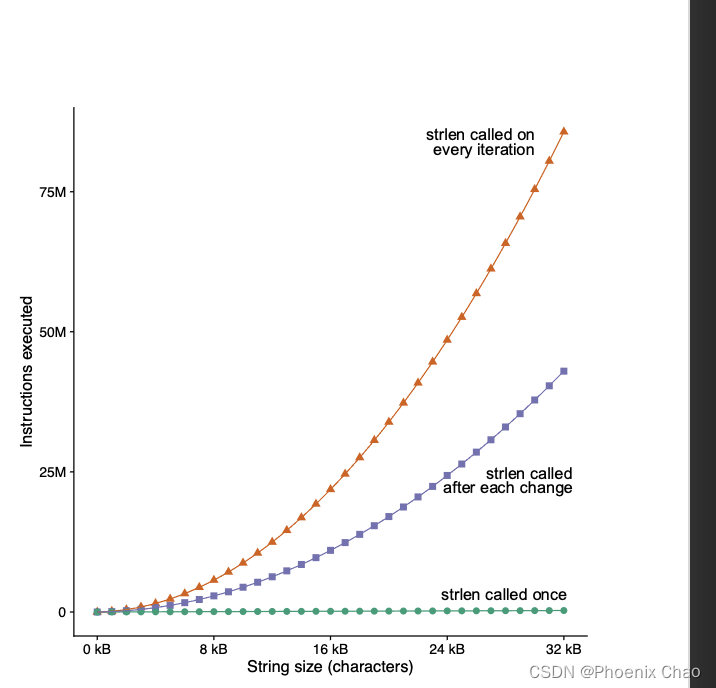
查阅strlen源码:

size_t strlen_a(const char *str) 
{ 
    size_t length = 0 ; 
    while (*str++ ) 
        ++ length; 
    return  length; 
}

strlen相当于每次扫描一遍字符串，然后返回length。本身的复杂度为O(n)。

而再加上for (i = 0; i < strlen(s); i++)需要扫描N次字符串s,因此总的复杂度是O($n^2$)。

如果不慎在程序中在循环中反复计算一个定值，也会出现类似的问题：

void lower_still_quadratic(char *s) {
  size_t i, n = strlen(s);
  for (i = 0; i < n; i++)
    if (s[i] >= 'A' && s[i] <= 'Z') {
      s[i] += 'a' - 'A';
      n = strlen(s);
    }
}

因此，优化的方法也很简单高效：

void lower_linear(char *s) {
  size_t i, n = strlen(s);
  for (i = 0; i < n; i++)
    if (s[i] >= 'A' && s[i] <= 'Z')
      s[i] += 'a' - 'A';
}

将O($n^2$)优化为O($n$)。

为什么编译器在编译的时候不会自动优化这个问题呢？

尽管有一个非常标准的strlen函数，但是程序并不一定在链接过程中使用标准strlen。因此编译器不能确定调用的就是这个strlen。

编译器只能假设strlen是一个黑盒子，并不能在此基础上做出任何优化。