算法学习笔记（一） 学不会的并查集

并查集被认为是最简洁而优雅的数据结构之一，并查集明明这么简洁而优雅，但我却学了这么久。。主要用于解决一些元素分组的问题。它管理一系列不相交的集合，并支持两种操作：

合并（Union）和查询（Find）

合并：把两个不相关的元素集合合并为一个集合。

查询：查询两个元素是否在同一个集合。

我们用图来形象说明并查集的原理。

首先所有元素各自在一个集合（自身是自身的父结点）

然后2 和3并入到1所属的集合（2和3把1当作父结点）

 接着4和5并入到6所属的集合（4和5把6当作父结点）

 

此时原先的6个集合变成了两个分别以1为父结点和6为父结点的集合。

此时我们再把6的父结点变为1

 

此时 6是4 5的父结点 1是2 3 6的父结点     1是2 3 4 5 6的根结点 1的结点是它本身。这时1 2 3 4 5 6在一个集合内。 

按照这个思路 可以写出简单版本的并查集代码。

初始化

int F[maxn]；
void init(int n)
{
    for(int i=1;i<=n;i++)
        fa[i]=i;//每个元素的父结点是自身
}

先将每个元素的父结点设为自己。

int find(int x)
{
    if(F[x]==x)
        return x;
    else 
        return find(F[x]);
}

通过递归的方式实现对元素的查询 ：一层层访问父结点直至根节点（根节点的特点是父结点是他本身）这样可以判断两个元素是否在同一个集合。

void Union(int i,int j)
{
    F[find(i)]=find[j];//将i节点的父结点变为j结点的父（根）结点
}

这样的并查集 由于查找通过递归的方式进行是很浪费时间 效率非常低的，因此要采取路径压缩

路径压缩

先举个例子来说明路径压缩的效果

 我们现在union(2,3）通过Find(2)；1将连接到3即F[1]=3，于是

 再来一个元素4  union(2,4）：

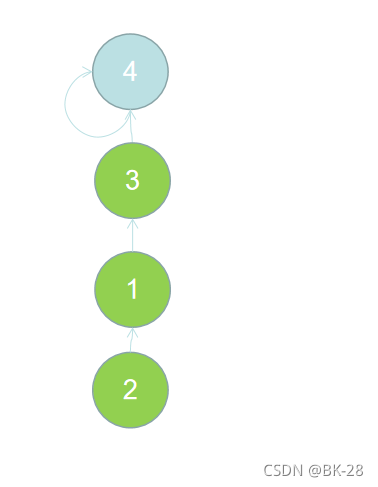
 会先从2找到1，再找到3，然后让F[3]=4;变成上图所示。

如果元素变多  会形成一条长长的链，会增加每次Find的时间。

而如果采用路径压缩，我们可以将每个元素只指向它的根节点 就像这样：

 这样每次查找就是一步到位省去很多时间。

int Find(int x)
{
    if(x==F[x])
        return x;
    else {
        F[x]=Find(F[x]);
        return F[x];
        }
}

按秩合并

现在 ，假设我们有一个复杂的树和一个单元素要和合并 ，我们选择union(7,8)，是将7设为节点更好还是8设为节点更好？

显然，将7作为8的节点更好，因为如果让8作为7的节点，会增加树的深度，这样查找就会耗时，就算使用路径压缩也是要浪费时间的。

这表明，在合并中，要尽可能将简单的树合并到复杂的树上，防止树的深度过长消耗不必要的时间。

我们用一个数组rank[]来记录根结点对应的树的深度（默认初始为1）。

这里要注意的是  路径压缩和秩一起用的时间复杂度接近O(n) ,但路径压缩会破坏rank的准确性使得树的结构被破坏。

初始化

void init(int n)
{
    for(int i=1;i<=n;i++)
    {
        F[i]=i;
        rank[i]=i;
    }
}

合并

void Union(int i,int j)
{
    int x=find(i),y=find(j);
    if(rank[x]<=rank[y])
        F[x]=y;
    else 
        F[y]=x;
    if(rank[x]==rank[y]&&x!=y)
        rank[y]++;                //如果深度相同但根节点不同  深度+1
}

例题

P1621 集合

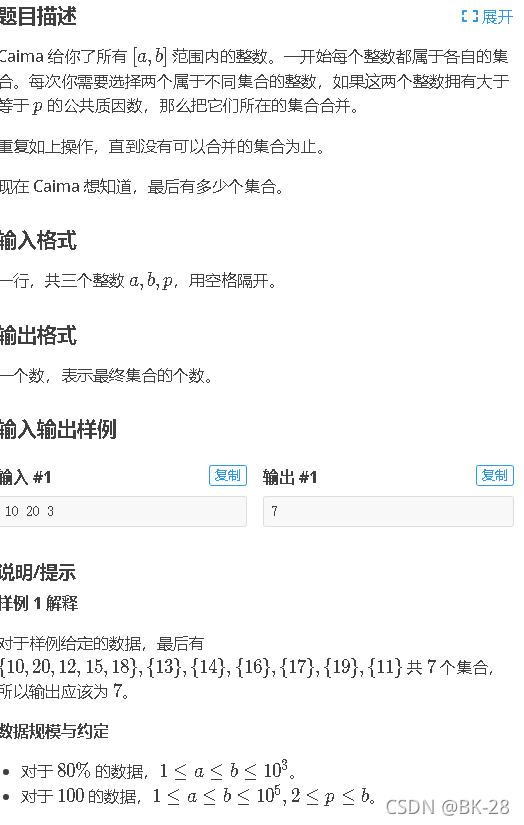
#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cmath>
#define maxn 100010
using namespace std;
int f[maxn];
int a,b,p,ans;
bool prime[maxn];
int vis[maxn];
int cnt;
int find(int x)
{
    if(f[x]==x) return x;
    else
    {
        f[x]=find(f[x]);
        return f[x];
    }
}
int Union(int x,int y)
{
    int t1=find(x),t2=find(y);
    if(t1!=t2)
    {
        f[t2]=t1;
        return 1;
    }
    return 0;
}
int make_prime()      //普通筛 
{
    memset(prime,1,sizeof(prime));
    int k=sqrt(b);
    prime[0]=prime[1]=0;
    for(int i=2;i<=k;i++)
        if(prime[i])
            for(int j=2*i;j<maxn;j+=i) prime[j]=0;
}
int main()
{
    cin>>a>>b>>p;
    for(int i=a;i<=b;i++) f[i]=i;
    make_prime();
    for(int i=p;i<=b;i++)      //找出p~b之间的素数 
        if(prime[i]) vis[++cnt]=i;  //记录 
    for(int i=1;i<=cnt;i++)     //找出a~b之间符合条件的数，合并 
    {
        int cc=0;
        while(cc*vis[i]<a) cc++;     //确保是a~b之间的，不要超范围，不然后面没法统计 
        while(vis[i]*(cc+1)<=b)
        {
            Union(vis[i]*cc,vis[i]*(cc+1));     //合并 
            cc++;
        }
    }
    for(int i=a;i<=b;i++)
        if(f[i]==i) ans++;     //统计个数 
    cout<<ans<<endl;
    return 0;
}