此为24年秋研究生课程复习笔记
相信魏老师！
最后的实际考题(有些数据不对，但题目形式一样)
-
设 f r ( n , k ) f_r(n,k) fr(n,k)是能够从集合 { 1 , 2 , ⋅ ⋅ ⋅ , n } \{1,2,···,n\} {1,2,⋅⋅⋅,n}中选出两两之差均大于r的k元子集的方案数，试求 f r ( n , k ) f_r(n,k) fr(n,k)。（原题）
-
从(0,0)点到达(m,n)点(m<n),要求中间所经过的每一个格子点(a,b)恒满足b>a，有多少条最短路径?（原题，但没点）
-
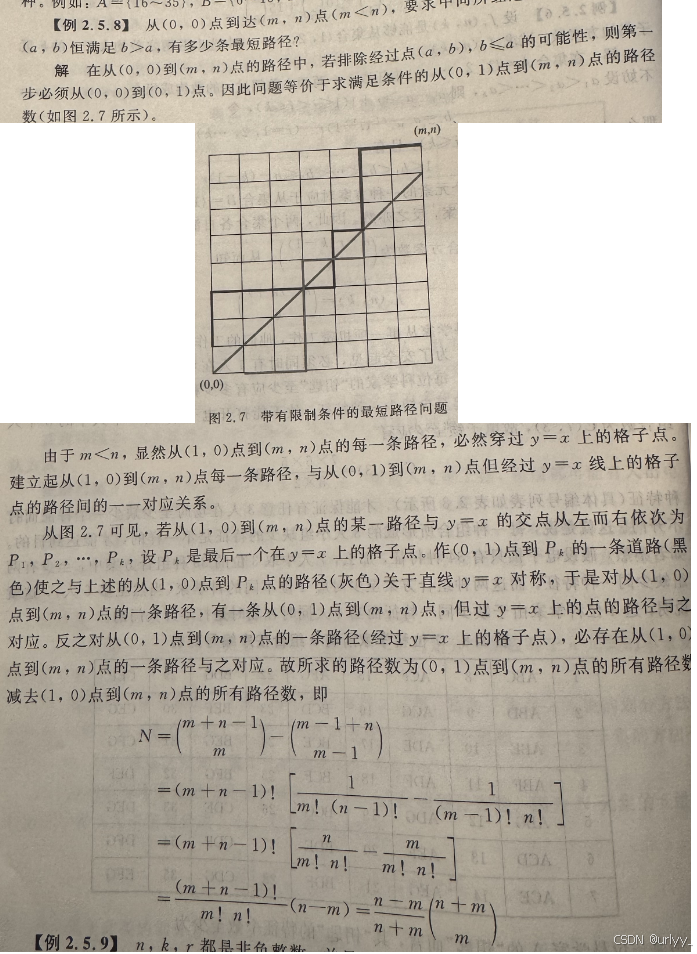
求1，3，5，7，9五个数字组成的n位数的个数（每个数字可重复出现），要求其中 3，7 出现的次数为偶数，1，5，9出现的次数不加限制。（好像考试改成了6个数字）
-
第i个棋子不能排在第 i 横行的第 i 个位置，问题可以看作在一个 n×n 的棋盘上，以对角线上的方格为禁区 A 的布局问题，求布局方案数。（就是错排概念的原题）
设A为禁区构成的棋盘。 R ( A ) = R ( □ ) ⋯ R ( □ ) = ( 1 + x ) n = ∑ k = 0 n C n k x k \mathrm{R(A)=~R(\square)~\cdots R(\square)=(1+x)^n}=\sum_{k=0}^nC_n^kx^k R(A)= R(□) ⋯R(□)=(1+x)n=∑k=0nCnkxk
即 r k ( A ) = C n k r_k\left(A\right)=C_n^k rk(A)=Cnk
根据容斥原理， D n = n ! – C n 1 ( n − 1 ) ! + C n 2 ( n − 2 ) ! − ⋯ + ( − 1 ) n C n n ( n − n ) ! D_n=n!–C_n^1(n-1)!+C_n^2(n-2)!-\cdots+(-1)^nC_n^n(n-n)! Dn=n!–Cn1(n−1)!+Cn2(n−2)!−⋯+(−1)nCnn(n−n)!
化简得 D n = n ! ( 1 − 1 1 ! + 1 2 ! − ⋯ + ( − 1 ) n 1 n ! ) D_n=n!\left(1-\frac1{1!}+\frac1{2!}-\cdots+\left(-1\right)^n\frac1{n!}\right) Dn=n!(1−1!1+2!1−⋯+(−1)nn!1) -
用红、黄、蓝三种颜色对正六边形的顶点进行着色，共有多少种不同的方案？其中正六边形可以绕几何中心旋转或沿其对称轴翻转。（原题）
-
设有4个元素的排列，其中要求第1个元素不能排在第1个位置，第2个元素不能在1、4号位置，元素3不能在2号、元素4不能在3号位置。问共有多少排列方案数？（这类题都是棋盘+逐步淘汰）
-
证明：任意给5个整数，其中必存在3个整数，其和能被3整除。（原题）
三个抽屉分别放对 3 取模为0/1/2的整数。如果有一个抽屉放了3个数，则存在和能被3整除的3个数，否则也可以三个抽屉各拿一个数，凑成和被3整除。如果n为5，则一定存在单个抽屉中整数个数大于等于3，否则单个抽屉最大为2个，即三个抽屉为2、2、1，即必存在3个满足的整数。而n为4时可能存在2、2、0的抽屉情况不满足要求。所以n最小为5。
-
求方程 x 1 + x 2 + x 3 ＝ 20 x_1+x_2+x_3＝20 x1+x2+x3＝20的整数解的个数，其中 2 ≤ x 1 ≤ 10 , 0 ≤ x 2 ≤ 7 , 3 ≤ x 3 ≤ 8 。 2\leq x_1\leq10\text{ ,}0\leq x_2\leq7\text{ , }3\leq x_3\leq8\text{ 。} 2≤x1≤10 ,0≤x2≤7 , 3≤x3≤8 。（改了数据）(容斥比母函数快)
-
h n = 3 h n − 1 − 4 n h_n=3h_{n-1}-4n hn=3hn−1−4n， h 0 = 2 h_0=2 h0=2(好像是?)，求通解。（递推关系，是第三种情况）
-
求1~1000的整数中不能被 5、6、8 整除的数的个数。(逐步淘汰，注意这题要考虑gcd)
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
