归并排序（Merge_sort）

一.基本原理

归并排序采用归并的思想来实现排序，该算法采用了经典的分治策略，把问题分成一些小的问题然后递归求解，而治的阶段则将分的阶段得到的各答案"修补"在一起，即分成子问题，递归处理子问题，合并子问题三部分。

二.排序过程

1.分

假设对下列8个数进行归并排序：

将已有数列不断分离成两段长度基本相同（奇数为一半短一半长）的数列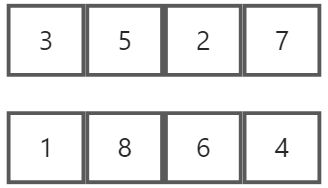

再分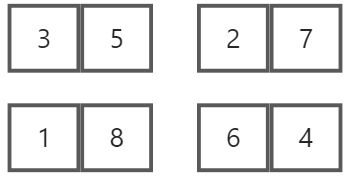

直至分离成长度为 1 的 8 个数列 ，即 8 个数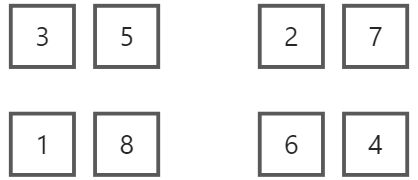

2.治

将分好的数列进行排序后合并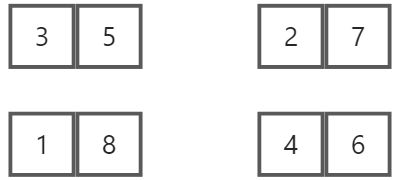

设置两个变量 i 和 j 对数列继续进行排序， 定义tmp数组，用于比较 i 和 j 所对应的两个数大小后暂时存入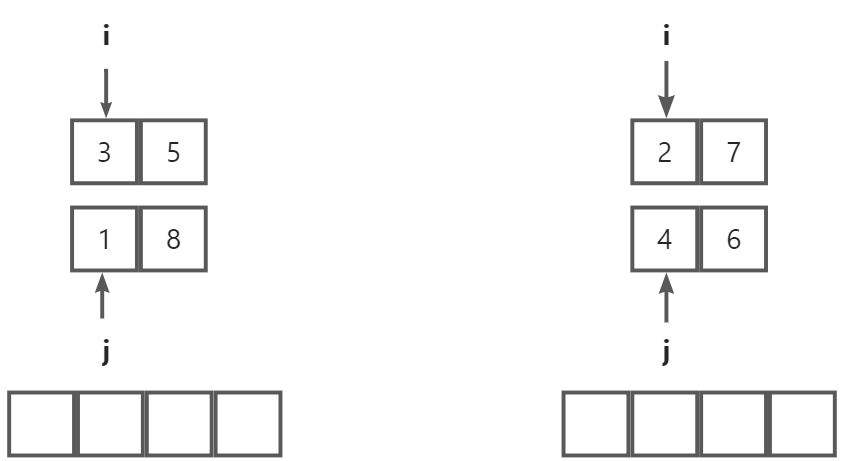

比较 i 和 j 所对应的两个数大小，将 i 和 j 中的较小数存入tmp数组，存入后 i 或 j 后移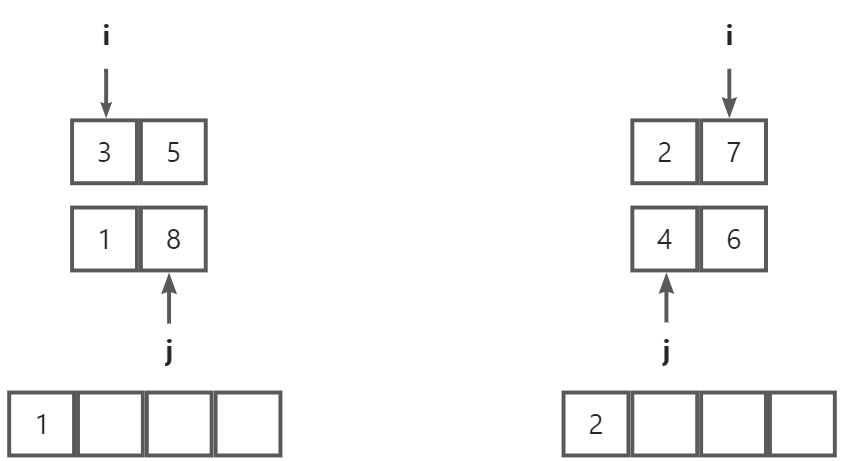

继续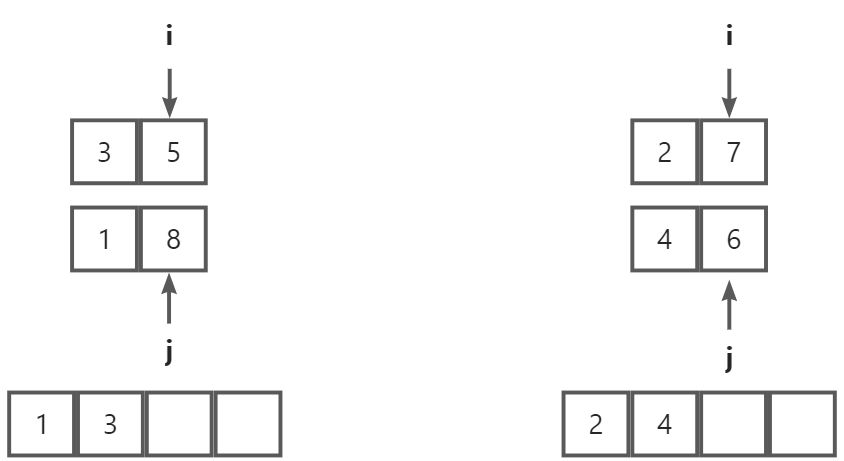

继续进行比较，此时其中一个数列已全部存入tmp数组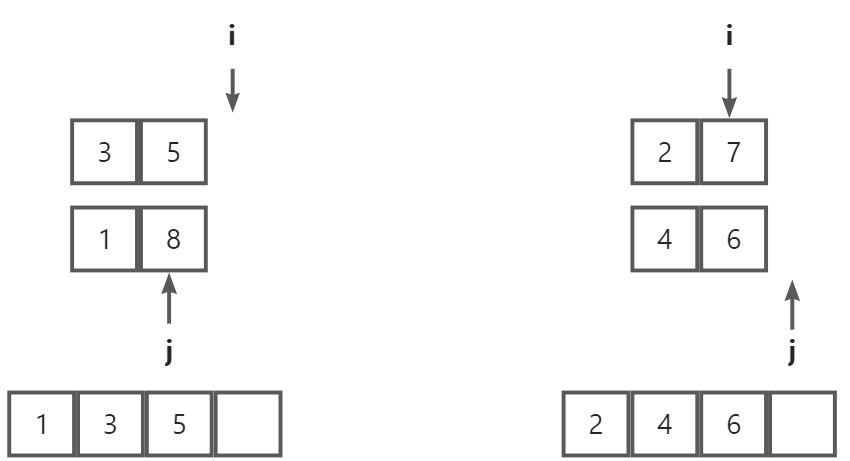

此时剩下数列中的数字直接赋给tmp数组，再将tmp数组赋给数组，可得到

继续递归，重复上述操作，即可得到

三.代码

const int N = 1e6 + 10;
int tmp[N];
void merge_sort(int q[], int l, int r)
{
    //递归终止条件
    if(l >= r)    
        return;
    //找中间值，将问题分成子问题
    int mid = l + r >> 1;    
    //递归处理子问题
    merge_sort(q, l, mid );
    merge_sort(q, mid + 1, r);
    //排序
    int k = 0, i = l, j = mid + 1;
    while(i <= mid && j <= r)
    {
        if(q[i] <= q[j]) 
            tmp[k++] = q[i++];
        else 
            tmp[k++] = q[j++];
    }
    //将剩余数赋给tmp数组
    while(i <= mid)
    { 
        tmp[k++] = q[i++];
    }
    while(j <= r)
    { 
        tmp[k++] = q[j++];
    }
    //合并
    for (i = l, j = 0; i <= r; i ++, j ++ )
    {
        q[i] = tmp[j];
    }
}