【编译原理】- 递归下降的语法分析器的实现

最新推荐文章于 2025-04-17 20:07:10 发布
最新推荐文章于 2025-04-17 20:07:10 发布
阅读量4k 收藏 63
点赞数 6
分类专栏： 编译原理 文章标签： c++
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_51795098/article/details/125505493
版权
本文介绍了如何使用递归下降法设计一个识别特定文法的语法分析器，处理包含十进制和十六进制数的表达式，并通过消除左递归和计算FIRST/FOLLOW集来确保LL(1)文法。作者提供了词法分析和主要数据结构的设计，以及源代码片段。

摘要生成于 C知道 ，由 DeepSeek-R1 满血版支持， 前往体验 >

目录

一、实验题目

二、分析与设计

三、源代码

一、实验题目

编写识别由下列文法G[E]所定义的表达式的递归下降语法分析器。

    EàE+T | E-T | T

    TàT*F | T/F |F

    Fà(E) | i

输入：含有十进制数或十六进制数的表达式，如：75+(1ah-3*2)+68/2#。

输出：语法正确或语法错误信息。

提示：

1）先用实验1代码将含有十进制数或十六进制数的表达式转换为对应的含i的表达式，例如75+(1ah-3*2)+68/2#转换为i+(i-i*i)+i/i#。

2）再对含i的表达式进行语法分析。

二、分析与设计

(1)   分析

a)        判断文法是否左递归，将文法改写为LL(1)文法

文法存在左递归

消除文法左递归：

E->TE’

E’->AE’|ε

A->+T|-T

T->FT’

T’->BT’|ε

B->*F|/F

F->(E)|i

b)       求FIRST与FOLLOW集

FIRST(E)={(,i}

FOLLOW(E)={ )，#}

FIRST(E’)={+,-,ε}

FOLLOW(E’)={ )，#}

FIRST(A)={+,-}

FOLLOW(A)={+，-，)，#}

FIRST(T)={(,i}

FOLLOW(T)={ +，-，)，#}

FIRST(T’)={*,/, ε}

FOLLOW(T’)={ +，-，)，#}

FIRST(B)={*,/}

FOLLOW(B)={*，/，+，-，)，#}

FIRST(F)={(,i}

FOLLOW(F)={ *，/，+，-，)，#}

c)        求SELECT集，并判断文法是否可以用递归下降分析法作语法分析

SELECT(E’->AE’)∩SELECT(E’->ε)={+,-}∩{},#}=Ø

SELECT(A->+T)∩SELECT(A->-T)={+}∩{-}=Ø

SELECT(T’->BT’)∩SELECT(T’->ε)={*,/}∩{+,-,},#}=Ø

SELECT(B->*F)∩SELECT(B->/F)={*}∩{/}=Ø

SELECT(F->(E))∩SELECT(F->i)={(}∩{i}=Ø

所以，该文法为LL(1)文法，可以用递归下降分析法作语法分析

(2)   设计

a)        主要数据结构及实现

全局变量：

char* q;//指向输入符号串中当前的字符

char word[20];//存储当前识别的单词

int state = 0;//表示所处的状态,初始状态为0

int i;//单词的下标

int j = 0;//输出数组out数组的下标

int wordErro = 1;//词法分析是否正确的标志,1:正确；0：错误

char sym;  //保存输入的字符

char line[30];  //保存读入的一行表达式

char out[30];   //保存词法分析后带i的表达式

int cur;  //表达式字符串的当前下标

int error;  //错误标志  0:正确  -1:错误

//利用这7个函数对应7个语法分析状态进行操作

int E(), E1(), T(), T1(), F();

b)       主要程序模块的算法流程图

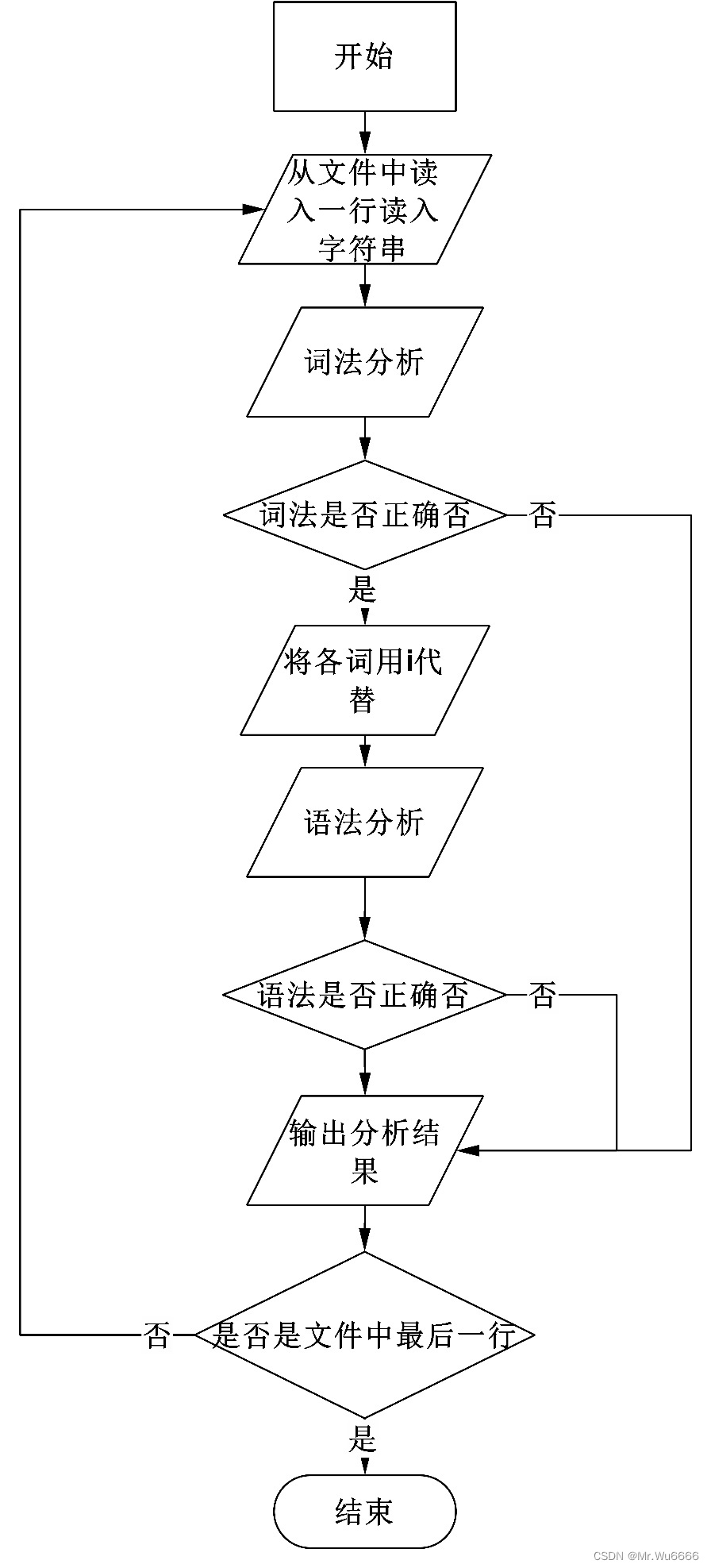
(3)   编码实现

(4)   上机调试

三、源代码

/*词法分析
  输入：包含十进制和十六进制的表达式
  输出：标准形式的表达式
  */

#include "stdio.h"
#include "string.h"
#include "conio.h"
#include<iostream>
using namespace std;

enum type { digit, Hh, AF, letter, oparetors };

char* q;//指向输入符号串中当前的字符
char word[20];//存储当前识别的单词
int state = 0;//表示所处的状态,初始状态为0
int i;//单词的下标
int j = 0;//输出数组out数组的下标
int wordErro = 1;//词法分析是否正确的标志,1:正确；0：错误

int isDigitOrChar(char ch) {
	if (ch >= 48 && ch <= 57)   //数字
		return digit;
	else if (ch == 72 || ch == 104)
		return Hh;              //Hh
	else if ((ch >= 65 && ch <= 70) || (ch >= 97 && ch <= 102))//ABCDEF或者abcdef
		return AF;
	else if ((ch >= 65 && ch <= 90) || (ch >= 97 && ch <= 122))//除A-F外的其他字母
		return letter;
	else if (ch == 40 || ch == 41 || ch == 42 || ch == 43 || ch == 45 || ch == 47 || ch == 35)//(、)、*、+、-、/ 、# 这六个运算符
		return oparetors;
}


int toExpress(char* words, char* out) {
	wordErro = 1;
	state = 0;
	i = 0;
	j = 0;
	printf("词法分析的结果为：");
	q = words;
	while (*q) {
		switch (state) {
		case 0:   //当前为0状态
			switch (isDigitOrChar(*q)) {
			case digit://数字
				word[i++] = *q;
				state = 2;
				break;
			case Hh:           //Hh
			case AF:           //ABCDEF或者abcdef
			case letter:       //除A-F外的其他字母
				word[i++] = *q;
				state = 1;
				break;
			case oparetors:        //运算符
				word[i++] = *q;
				printf("%c", word[0]);
				out[j++] = word[0];
				state = 0;
				memset(word, 0, sizeof(word));
				i = 0;
				break;
			default:           //其他字符（非法）
				word[i++] = *q;
				state = 5;     //转到出错状态
				break;
			}
			break;
		case 1:   //当前为1状态
			switch (isDigitOrChar(*q)) {
			case digit://数字
				word[i++] = *q;
				state = 1;
				break;
			case Hh:           //Hh
			case AF:           //ABCDEF或者abcdef
			case letter:       //除A-F外的其他字母
				word[i++] = *q;
				state = 1;
				break;
			case oparetors:        //运算符,1状态可以为标识符的结束状态
				word[i++] = *q;
				state = 0;
				printf("i");
				out[j++] = 'i';
				for (int m = 0;m < sizeof(word);m++) {
					if (isDigitOrChar(word[m]) == oparetors) {
						printf("%c", word[m]);
						out[j++] = word[m];
					}
				}
				memset(word, 0, sizeof(word));
				i = 0;
				break;
			default:           //其他字符（非法）
				word[i++] = *q;
				state = 5;     //转到出错状态
				break;
			}
			break;
		case 2:   //当前为2状态
			switch (isDigitOrChar(*q)) {
			case digit://数字
				word[i++] = *q;
				state = 2;
				break;
			case Hh:           //Hh
				word[i++] = *q;
				state = 3;
				break;
			case AF:           //ABCDEF或者abcdef
				word[i++] = *q;
				state = 4;
				break;
			case oparetors:        //运算符,2状态可以为十进制整数的结束状态
				word[i++] = *q;
				state = 0;
				printf("i");
				out[j++] = 'i';
				for (int m = 0;m < sizeof(word);m++) {
					if (isDigitOrChar(word[m]) == oparetors) {
						printf("%c", word[m]);
						out[j++] = word[m];
					}
				}
				memset(word, 0, sizeof(word));
				i = 0;
				break;
			default:           //其他字符（非法）
				word[i++] = *q;
				state = 5;     //转到出错状态
				break;
			}
			break;
		case 3:   //当前为3状态
			switch (isDigitOrChar(*q)) {
			case oparetors:        //运算符,3状态可以为十六进制整数的结束状态
				word[i++] = *q;
				state = 0;
				printf("i");
				out[j++] = 'i';
				for (int m = 0;m < sizeof(word);m++) {
					if (isDigitOrChar(word[m]) == oparetors) {
						printf("%c", word[m]);
						out[j++] = word[m];
					}
				}
				memset(word, 0, sizeof(word));
				i = 0;
				break;
			default:           //其他字符（非法）
				word[i++] = *q;
				state = 5;
				break;
			}
			break;
		case 4:   //当前为4状态
			switch (isDigitOrChar(*q)) {
			case digit://数字
				word[i++] = *q;
				state = 4;
				break;
			case Hh:           //Hh
				word[i++] = *q;
				state = 3;
				break;
			case AF:           //ABCDEF或者abcdef
				word[i++] = *q;
				state = 4;
				break;
			default:           //其他字符（非法）
				word[i++] = *q;
				state = 5;     //转到出错状态
				break;
			}
			break;
		case 5:   //出错状态
			switch (isDigitOrChar(*q)) {
			case oparetors:        //运算符
				word[i++] = *q;
				state = 0;
				memset(word, 0, sizeof(word));
				i = 0;
				wordErro = 0;
				break;
			default:           //其他字符（非法）
				word[i++] = *q;
				state = 5;     //转到出错状态
				break;
			}
			break;
		}
		q++;     //指针下移（指向输入符号串的下一个字符）
	}
	if (wordErro == 1) {
        printf("\n》》》词法正确！《《《\n");
	}
	else {
		printf("\n》》》词法错误！《《《\n");
	}
	
	return 0;
}


/*从test.txt文件中读入由i和运算符组成的式子，
  判断是否合法
*/

char sym;  //保存输入的字符
char line[30];  //保存读入的一行表达式
char out[30];   //保存词法分析后带i的表达式
int cur;  //表达式字符串的当前下标
int error;  //错误标志  0:正确  -1:错误

//声明函数
int E(), E1(), T(), T1(), F();

//读入当前字符
char read(char line[], int k) {
	return line[k];
}

int E() {
	T();
	E1();
	return 0;
}

int E1() {
	if (sym == '+' || sym == '-') {
		cur++;
		sym = read(line, cur);
		T();
		E1();
	}
	else if (sym == '#' || sym == ')') {
		return 0;
	}
	else {
		error = -1;
	}
	return 0;
}

int T() {
	F();
	T1();
	return 0;
}

int T1() {
	if (sym == '*' || sym == '/') {
		cur++;
		sym = read(line, cur);
		F();
		T1();
	}
	else if (sym == '+' || sym == ')' || sym == '#' || sym == '-') {
		return 0;
	}
	else {
		error = -1;
	}
	return 0;
}

int F() {
	if (sym == 'i') {
		cur++;
		sym = read(line, cur);
	}
	else if (sym == '(') {
		cur++;
		sym = read(line, cur);
		E();
		if (sym == ')') {
			cur++;
			sym = read(line, cur);
		}
		else {
			error = -1;
		}
	}
	else {
		error = -1;
	}
	return 0;
}

int main(int argc, char* argv[]) {
	FILE* fp;
	//打开文本文件
	fopen_s(&fp, "C:/Users/wzy/Desktop/编译原理实验2 -测试用例-test.txt", "r");
	if (fp == NULL) {
		printf("open file error!\n");
		getchar();
		return -1;
	}
	//逐行读入表达式，并分析是否符合语法规则
	while (!feof(fp)) {
		printf("------------------------------------------\n");
		strcpy_s(line, "\0");
		fscanf_s(fp, "%s", &line, 30); //逐行读
		cur = 0;
		error = 0;
		printf("输入字符串为：%s \n", line);
		char inputString[30];//中间变量，存储输入的字符串
		for (int i = 0;i < sizeof(line);i++) {
			inputString[i] = line[i];
		}
		//进行词法分析
		toExpress(line, out);
		memset(line, 0, sizeof(line));
		for (int i = 0;i < sizeof(line);i++) {
			line[i]= out[i];
		}
		if (wordErro == 1) {//若词法正确，则进行语法分析
			sym = read(line, cur);//读入当前字符
			E();//开始语法分析
			//如果表达式有错
			if (error == -1) {
				printf("》》》语法错误！《《《\n分析结果：%s为非法字符串\n", inputString);
				printf("------------------------------------------\n");
			}
			//如果表达式合法
			else if (error == 0) {
				printf("》》》语法正确！《《《\n分析结果：%s为合法字符串\n", inputString);
				printf("------------------------------------------\n");
			}
			memset(line, 0, sizeof(line));
			memset(out, 0, sizeof(out));
			wordErro = 1;
		}
		else{
			printf("》》》不进行语法分析！！《《《\n分析结果：%s为非法字符串\n", inputString);
			printf("------------------------------------------\n");
			continue;
		}
	}
	fclose(fp);
	getchar();
	return 0;
}

test.txt中的内容（测试用例）：

80+5eH+(6+1h)*2+4h#
6+(5+2))*5+80bh#
95eah+3*(5+10)+35h#
9*6+(5+2)*5+80bh#
59h+((3+9ah)*3+4#
7+9*2#

【编译原理与技术】递归下降语法分析器（C++实现）
Slimshady的博客
06-26 1万+
目录内容：示例：具体实现：C++代码：运行结果： 内容： 实现以下语法的递归下降分析： 示例： 对于以下代码给出其递归下降语法分析过程： { i=2; while(i<=100) { sum=sum+i; i=i+2; } } 具体实现： 首先对上下文无关文法进行检查，消除左递归和左公共因子，从逻辑上检测避免死循环和低效率处理。 采用每个产生式的左边的文法符号对应一...
递归下降语法分析器
05-08
c语言编写的递归下降语法分析器的算法，测试成功可以直接跑代码
递归下降分析器的设计
最新发布
m0_73097474的博客
04-17 610
（仅供参考）
递归下降语法分析器的实现
05-09
递归下降语法分析器的实现递归下降语法分析器的实现递归下降语法分析器的实现递归下降语法分析器的实现递归下降语法分析器的实现
语法分析器(递归下降分析)
01-08
语法分析器 递归下降分析 Java语言编写 良好图形界面 * 原始文法 * E->E+T|E-T|T * T->T*F|T/F|F * F->(E)|i
编译原理——语法分析器（递归下降分析法 ）
05-05
递归下降分析法 一、实验目的： 根据某一文法编制调试递归下降分析程序，以便对任意输入的符号串进行分析。本次实验的目的主要是加深对递归下降分析法的理解。 二、实验说明 1、递归下降分析法的功能 词法分析器的功能是利用函数之间的递归调用模拟语法树自上而下的构造过程。 2、递归下降分析法的前提 改造文法：消除二义性、消除左递归、提取左因子，判断是否为LL（1）文法， 3、递归下降分析法实验设计思想及算法 为G的每个非终结符号U构造一个递归过程,不妨命名为U。 U的产生式的右边指出这个过程的代码结构： (1)若是终结符号，则和向前看符号对照， 若匹配则向前进一个符号；否则出错。 (2)若是非终结符号，则调用与此非终结符对应的过程。当A的右部有多个产生式时,可用选择结构实现。 三、实验要求 （一）准备： 1.阅读课本有关章节， 2.考虑好设计方案； 3.设计出模块结构、测试数据，初步编制好程序。 （二）上课上机： 将源代码拷贝到机上调试，发现错误，再修改完善。第二次上机调试通过。 （三）程序要求： 程序输入/输出示例： 对下列文法，用递归下降分析法对任意输入的符号串进行分析： （1）E->eBaA （2）A->a|bAcB （3）B->dEd|aC （4）C->e|dc 输出的格式如下： (1)递归下降分析程序，编制人：姓名，学号，班级 (2)输入一以#结束的符号串：在此位置输入符号串例如：eadeaa# (3)输出结果：eadeaa#为合法符号串 注意： 1.如果遇到错误的表达式，应输出错误提示信息（该信息越详细越好）； 2.对学有余力的同学，可以详细的输出推导的过程，即详细列出每一步使用的产生式。 （四）程序思路 0.定义部分：定义常量、变量、数据结构。 1.初始化：从文件将输入符号串输入到字符缓冲区中。 2.利用递归下降分析法分析，对每个非终结符编写函数，在主函数中调用文法开始符号的函数。
递归下降法实现语法分析器（java）
08-09
递归下降法实现语法分析器源代码（java语言编写），将src文件导入eclipse工程即可运行处结果。
编译原理课设：属性计算-递归下降语法分析器
07-11
设计递归下降翻译器，完成语法分析和中间代码翻译。 输入：一个完整的源程序 输出：与输入对应的一个语法树、四元式序列 2、资源 课设报告word 课设源码 3、开发环境 编程语言：C++ IDE：VS 2019
编译原理实验-递归下降的方法实现语法分析器
09-22
（使用Python实现，注释详尽）在词法分析器的基础上，采用递归下降的方法实现算术表达式的语法分析器，以加深对自上而下语法分析过程的理解。 1、对算术表达式文法： E→TE' E'→+TE'| -TE' |ε T→FT' T'→*FT'| /...
编译原理 递归下降语法分析程序（代码+说明文档）
07-10
在编译原理中，递归下降语法分析程序是一种基于自顶向下分析方法的解析技术，它主要用于理解程序源代码的结构并将其转化为抽象语法树（AST）。本资源包含了一个递归下降语法分析程序的实现，以及相关的说明文档，...
递归下降语法分析器设计
04-18
一个关于递归下降语法分析器设计的文档
用java语言编写的递归下降语法分析器
05-04
用java语言编写的递归下降语法分析器用java语言编写的递归下降语法分析器用java语言编写的递归下降语法分析器
编译实验三 递归下降的语法分析器
04-14
是利用FLEX生成的词法分析器，调用YYLEX()来实现token的获取。
北交-编译原理实验-递归下降语法分析设计原理与实现技术内含源码和说明书.zip
05-12
《编译原理实验：递归下降语法分析设计与实现》 在计算机科学领域，编译原理是理解程序设计语言如何转换为机器可执行代码的关键部分。本实验主要聚焦于递归下降语法分析的设计与实现，这是一个重要的编译器构造技术...
编译原理 --- 递归下降分析器
qq_51947882的博客
10-19 3184
1.在上面这个例子中则是子程序序A先调用子程序B，本程序结束完调用之后再返回来继续调用下一个符号如果下一个符号是终结符的话那就直接进行匹配，不进行调用，匹配完后继续调用下一个符号如果不是的话则调用这个非终结符对应的子程序，并重复步骤 1 1.ADVANCE是一个字程序，作用是输入下一个符号2.SYM则是指向当前输入的单词符号1.一个非终结符的展开就等价于调用这个非终结符对应的语法分析子程序1.一个非终结符对应的子程序就用这个非终结符本身来命名，比如非终结符A的子程序的命名就是A本身2.上面这个设计中的Beg
手把手教你使用递归下降法实现语法分析器
热门推荐
qq_44075108的博客
11-16 1万+
对下列算术表达式的文法编写递归下降分析程序，要求对输入的任意符号串进行语法分析： （1）E->TE' （2）E'->+TE' | —TE' |ε （3）T->FT' （4）T'->*FT' | /FT' |ε （5）F->(E) | id | num 注：文法中id表示标识符（此处标识符的定义与实验一中标识符的定义相同），num表示数字（简单处理可以认为是整数）
编写递归下降语法分析器
12-30
### 编写递归下降语法分析器 #### 定义文法并消除左递归 为了创建有效的递归下降解析器，首先要定义目标语言的上下文无关文法(CFG)，并且要确保该文法不含有直接或间接的左递归。这是因为递归下降解析器对于左递归会产生无限循环[^2]。 例如，考虑一个简单的算术表达式文法： - E → T | E + T - T → F | T * F - F → (E) | id 上述文法规则存在左递归问题，因此需要转换成无左递归的形式: - E → TE' - E'→ +TE'| ε - T → FT' - T'→ *FT'| ε - F → (E)|id #### 计算First集和Follow集 在处理LL(1)文法时，计算每个非终结符的`FIRST`集合以及`FOLLOW`集合是非常重要的。这有助于决定何时调用特定的过程来匹配输入字符串的一部分。 #### 设计预测表驱动的函数 基于修改后的文法，为每一个非终结符编写对应的解析过程。这些过程通常会尝试读取当前符号，并根据它应该做什么动作做出决策。如果遇到预期之外的情况，则抛出异常表示解析失败[^3]。 下面是一个简化版的例子，展示了如何用JavaScript实现部分功能： ```javascript function match(tokenType){ if(tokens[currentIndex].type === tokenType){ currentIndex++; }else{ throw new Error(`Unexpected token at position ${currentIndex}`); } } // 对应于文法中的E -> TE’ function expr(){ term(); exprPrime(); } // 对应于文法中的E’-> +TE’|ε function exprPrime(){ let currentToken = tokens[currentIndex]; if(currentToken.type === 'PLUS'){ match('PLUS'); term(); exprPrime(); }// else epsilon transition, do nothing. } ``` 此代码片段仅实现了加号运算的部分逻辑，完整的解决方案还需要加入其他操作符的支持以及其他辅助方法如`term()` 和 `factor()` 的定义[^1]。
评论 2
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值