【算法基础】排列组合C（n,m）算法优化过程不溢出

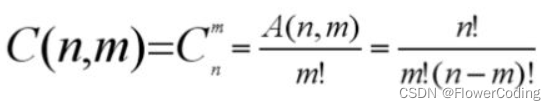
传统思维方法：

long long cal(int n,int m)
{
    long low = 1;
    for(int i = 1; i <= n; i++)
    {
        low *= i;
    }
    long up = 1;
    for(int j = n-1; j >= 0; j--)
    {
        up *= (m-j);
    }
    return up/low;
}

这种传统解法看上去符合逻辑，实则数稍微一大就会过程溢出，不用太大，n == 100，m == 100就崩了。

PS：不需要担心除不尽的问题，联系排列组合的实际意义，它是在m中取n个有多少种取法，是不会有小数的。

优化算法：

为了防止过程溢出，不能让计算过程的数字太大，所以分子分母同时发力，分子乘一位分母除一位。

long long cal(int n,int m)
{
    long long ans = 1;
    for(int i = 1; i <= n; i++)
    {
        ans *= m--;
        ans /= i;
    }
    return ans;
}

这个方法乘一位就除一位，防止了过程溢出，但是样例不能太大，不然就超过了计算机所能处理的数据范围。

PS：可能有人会问这样不会除不尽，ans乘以第一位的时候，因为ans除的是1（相当于没有除），一定能除尽；ans乘以第二位的时候，由于ans已经乘了相邻的两个数了，一定会出现一个2的倍数，所以除以2也能整除；ans乘以第三位的时候，由于ans已经乘了相邻的三个数了，一定会出现一个3的倍数，所以除以3也能整除......依次类推，最后一定能整除！（可能一个数字的出现可能是是多个数字的倍数，比如一个数字是3的倍数也是2的倍数，完全不影响的，可以写成2*3*n，n也可能是一个或多个除数的倍数）