数学建模——非线性规划

最新推荐文章于 2024-07-14 23:58:50 发布

原创最新推荐文章于 2024-07-14 23:58:50 发布 · 685 阅读

3 ·

CC 4.0 BY-SA版权

文章标签：

#数学建模 #线性规划 #matlab

非线性规划问题：目标函数或约束条件中包含非线性函数。

非线性规划目前没有适用于各种问题的一般算法，各个方法有自己特点的适用范围。

本文采用Matlab进行非线性规划求解：

一元函数的极值求解（fminbnd函数）

x=fminbnd(fun,a,b)

fun：一元函数。[a,b]为函数自变量的取值范围。

求函数fun在区间[a,b]上的极小值点。

要求：必须是连续的函数，只能给出局部极小解

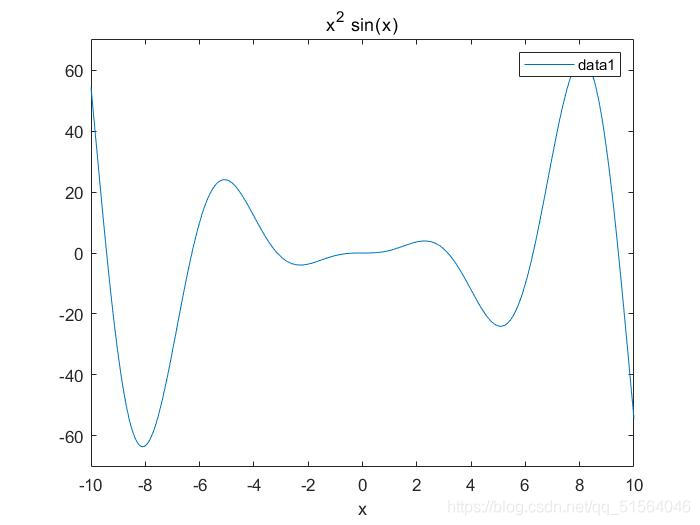
求函数 $f(x)=x^{2}sin(x)$ 在区间[-10,10]内的极小值点。

clear all;
f='x^2*sin(x)';
ezplot(f,[-10,10]);
[xmin,ymin]=fminbnd(f,-10,10)
f1='-x^2*sin(x)';
[xmax,yval]=fminbnd(f1,-10,10)

xmin =3.9270
ymin =-0.0279
xmax =0.7854
yval =-0.6448

多元函数的极值求解（fminsearch函数）

eg：求函数 $f=-(x+y)+(x^{2}+y^{2}+1)$ 在x=1,y=2附近的最小值点。

1.建立M文件保存函数fun2.m；

function f2=fun2(x)
f2=-(x(1)+x(2))+(x(1)^2+x(2)^2+1);

2.在命令窗口输入：

x0=[1,2];
[x,fval]=fminsearch(@fun2,x0)

3.得到结果

约束非线性优化问题（fmincon函数）

[x,fval]=fmincon(fun,x0,A,b,Ae,be,lb,ub,nonlcon)

x表示最优解，fval表示最优函数值。

fun为目标函数，A，b表示满足线性关系 $Ax\leqslant b$ 的系数矩阵和右端项；Ae，be表示等式的系数矩阵和右端项。lb,ub表示取值范围的上界和下限。nonlcon表示需要参数满足的非线性关系。

eg:

1.建立函数funeg.m;(目标函数)

function f_eg=funeg(x);
f_eg=(-5000-7*x(1))*x(1)+(-1000-10*x(2))*x(2);

2.建立函数fun_test.m（限制函数）

%{
华艺公司租用三种设备A,B,C生产I，II两种产品
        设备A     设备B     设别C
产品1       3        2        15
产品2       4        1         2
可用工时  1600     600       750
其中产品2生产量不低于两种产品总产量的30%。不超过60%。
两种产品的需求量x1，x2是其价格P1，P2的函数：
x1=5000-7P1
x2=1000-10P2
综合考虑需求和价格，使预期总销售价为最大
%}
function [g,h]=fun_test(x);
g=[3*(5000-7*x(1))+4*(1000-10*x(2))-1600;
    2*(5000-7*x(1))+1000-10*x(2)-600;
    15*(5000-7*x(1))+2*(1000-10*x(2))-750];
h=[];

3.利用fmincon函数求解

[x,y]=fmincon('funeg',rand(2,1),[],[],[],[],zeros(2,1),[],'fun_test')

得到结果。