LeetCode 5955. 摘水果题目解析

秋刀鱼与猫_

已于 2022-05-06 22:05:03 修改

阅读量5.4k

点赞数 3

分类专栏：力扣精选题文章标签： leetcode 算法职场和发展

于 2021-12-12 16:02:47 首次发布

本文链接：https://blog.youkuaiyun.com/qq_51439643/article/details/121888952

版权

力扣精选题专栏收录该内容

9 篇文章

订阅专栏

本文解析了一道关于动态规划与搜索技巧的LeetCode题目，关键在于理解移动方向的唯一改变和利用前缀和数组快速计算路径价值，结合二分查找确定转向后的最大收获。通过实例演示和代码实现，展示了如何在K次移动中获取最大水果数。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

LeetCode 5955. 摘水果 ⭐️⭐️⭐️⭐️⭐️

5955. 摘水果 #前缀和 #二分查找

1、题目解析

这是LeetCode周赛中的最后一题，也是我觉得迄今为止离AC最近的一次😢

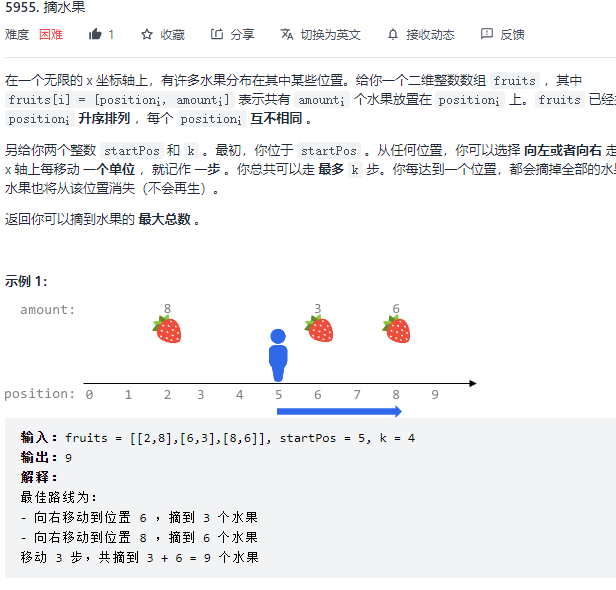
题目很好理解，在最多K次的移动中获取水果的最大值将其返回。

开始的思路是动态规划还有搜索，但是限于水平有限也没有动规出啥东西反而时间浪费了

这道题的核心是要理解：移动的过程中最多改变一次移动的方向

也就是说只要枚举出坐标轴中所有的水果改变方向前、改变方向后的最大总数之和就是我们需要求的值。

例如水果分别在0、6、7位置上出发点为3，k=10

假设在0出改变方向，出发点到0位置需要3步剩余7，改变位置后人物只会向右方移动，移动的最远距离为7，途中可以采集位于6的水果。在6、7处改变方向也同理，这里不过多赘述。

那么如何快速获取在移动到某点能收获的数量呢？每一次经过水果后相加时间复杂度高得吓人，这里可以使用前缀和数组，通过前缀和性质能够快速获得值。

那么如何获取每次转向后最终能够收集的水果索引呢？因为索引编号递增，因此可以使用二分查找的方式。如下代码中定义了upperBound查找第一个大于key的索引下标，lowerBound查找第一个大于等于key的索引下标。

因此在代码中，所有的移动方式，先向右移动然后返回向左或先向左移动返回后向右，保存每次移动后获得的最大值，即使答案。

2、代码

class Solution {
    public int upperBound(int []pos,int l,int r,int key){
        while(l<r){
            int m = (l+r)/2;
            if(pos[m]>key){
                r=m;
            }
            else{
                l=m+1;
            }
        }
        return  l;
    }
    public int lowerBound(int []pos,int l,int r,int key){
        while(l<r){
            int m = (l+r)/2;
            if(pos[m]>=key){
                r=m;
            }
            else{
                l=m+1;
            }
        }
        return l;
    }
    public int maxTotalFruits(int[][] fruits, int startPos, int k) {
        List<Integer>sum=new ArrayList<>();
        int ans=0;
        sum.add(0);
        int n=fruits.length;
        for(int i=1;i<=n;++i){
            sum.add(sum.get(i-1)+fruits[i-1][1]);
        }
        int []pos=new int[n];
        for(int i=0;i<n;++i){
            pos[i]=fruits[i][0];
        }
        for(int red=k;red>=0;--red){
            // 折返距离因此需要除以2
            int dis=(k-red)/2;
            int l,r,lw,rw;
            // 先向左移动
            l=startPos-dis;
            r=startPos+red;
            lw=sum.get(lowerBound(pos,0,n,l));
            rw=sum.get(upperBound(pos,0,n,r));
            ans=Math.max(ans,rw-lw);

            // 先向右移动
            r=startPos+dis;
            l=startPos-red;
            lw=sum.get(lowerBound(pos,0,n,l));
            rw=sum.get(upperBound(pos,0,n,r));
            ans=Math.max(ans,rw-lw);
        }
        return ans;
    }
}