数据挖掘课程笔记（不断更新）

数学基础

线性代数基础

向量

$$\vec{X}$$
（1）长度
（2）方向
转置
$${\vec{X}}^T$$
内积
$${\vec{X}}^T\vec{X}$$
外积
$$\vec{X}{\vec{X}}^T\in R$$
投影算子
范数
$$||\vec{X}||=\sqrt[]{{\vec{X}}^T\vec{X}}$$

矩阵

$$A=\left[\begin{array}{ccc}& & \\ & & \\ & & \end{array}\right]$$

$$A\in R^{m\times n}$$
定义在实数域
作用：改变原来矢量的长度、方向

转置
$$A=\left[\begin{array}{cc}1& 2\\ 3& 4\end{array}\right]A^T=\left[\begin{array}{cc}1& 3\\ 2& 4\end{array}\right]$$

矩阵乘法

计算：
$$AB=\left[\begin{array}{ccc}2& 3& \\ 1& 4& \end{array}\right]\left[\begin{array}{ccc}1& 1& \\ 1& 1& \end{array}\right]$$

矩阵运算

(1)加减
$$A\pm B$$
（2）乘积

内积
外积

（3）张量积

矩阵运算法则

(1)乘法
$$AB\ne BA$$
(2)结合律
$$(AB)C=A(BC)$$
(3)分配律
$$A(B+C)=AB+AC$$

单位矩阵 I
$$I=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$
$$AI=IA=A$$

纯量矩阵
$$k\left[\begin{array}{ccc}1& 1& 1\\ 1& 1& 1\\ 1& 1& 1\end{array}\right]$$

矩阵的转置
$$(A^T{)}^T=A$$
$$(AB{)}^T=A^T{B}^T$$
$$(A+B{)}^T=A^T+B^T$$

矩阵的迹

求矩阵A的迹主要用两种方法：
1.迹是所有对角元的和,就是矩阵A的对角线上所有元素的和
$$tr(A)=\sum _{i=1}^n{a}_{ii}$$
2.迹是所有特征值的和,通过求出矩阵A的所有特征值来求出它的迹.
$$tr(A)=tr(A^T)\text{\hspace{1em}(1)}$$

$$tr(A+B)=tr(A)+tr(A)\text{\hspace{1em}(2)}$$

$$tr(tA)=ttr(A)\text{\hspace{1em}(3)}$$

$$tr(AB)=tr(BA)\text{\hspace{1em}(4)}$$
符合（2）（3）的即为线性
计算：
$$\left[\begin{array}{ccc}3& 1& 4\\ 2& 1& 3\\ 1& 4& 5\end{array}\right]$$
范数

二范数是通过内积定义的
$$L_2=\sqrt[2]{{\vec{X}}^T\vec{X}}$$
一范数
$$L_1=\sum |x_i|$$
无穷范数
$$L_{\infty }=max(|x_i|)$$
P范数
$$L_p={\sum _{i=1}^n{(|x_i|}^p)}^{1/p}$$

线性相关&线性不相关

给定集合 s e t { x 1 , x 2 , … x n } set\left\{x_1,x_2,…x_n\right\} set{x1​,x2​,…xn​}
$$x_n=\sum _{i-1}^{n-1}{\alpha }_i{x}_i$$

秩

n✖️n 行秩 = 列秩
性质
（1）$$rank(A)=rank(A^T)$$
（2）$$rank(AB)<=min(rank(A),rank(B))$$
（3）$$rank(A+B)<=rank(A)+rank(B)$$

逆

$$A^{-1}A=I=A{A}^{-1}$$
(1)$${(A^{-1})}^{-1}=A$$
(2)$$Ax=b<<=>>x=A^{-1}b$$
(3)$${AB}^{-1}=B^{-1}{A}^{-1}$$
(4)$${(A^{-1})}^T={(A^T)}^{-1}$$

正交矩阵

若一个矩阵U：有$$U^{T}U=I$$ 则 $$U^T=U^{-1}$$

张成空间与投影

略

机器学习

监督学习

经典例题：房价预测
假设我们有一个数据集，给出了来自俄勒冈州波特兰市的47栋房子的生活区和价格：
根据这样的数据，我们如何学会预测波特兰其他房屋的价格，作为他们居住面积大小的函数？
为了建立将来使用的符号，我们将使用$x^{(i)}$表示“输入”变量（也称为输入特征）（本例中的居住区域），$y^{(i)}$表示我们试图预测的“输出”或目标变量。一对$(x^{(i)},y^{(i)})$被称为训练示例，我们将用来学习的数据集是m个训练示例$\{(x^{(i)},y^{(i)});i=1,\dots ,m\}$被称为训练集。注意：符号中的上标“$(i)$”只是进入训练集的一个索引，与指数化无关。我们还将使用$\mathcal{X}$表示输入值的空间，$\mathcal{Y}$表示输出值的空间。在这个例子中，$\mathcal{X}=\mathcal{Y}=\mathbb{R}$。
为了更正式地描述监督学习问题，我们的目标是，给定一个训练集，学习函数$h:\mathcal{X}\mapsto \mathcal{Y}$，这样$h(x)$是对应值的一个“好”预测器。由于历史原因，这个函数$h$被称为假设。从图片上看，这个过程是这样的：

当我们试图预测的目标变量是连续的时，我们称学习问题为回归问题（比如在我们的住房例子中）。当$y$只能接受少量的离散值时，我们称之为分类问题（比如给定生活区，我们想要预测一个住宅是房子还是公寓）。

第一部分

线性回归（Linear Regression）

为了让我们的住宅示例更有趣，让我们考虑一个稍微丰富一些的数据集，其中我们也知道每栋房子的卧室数量：

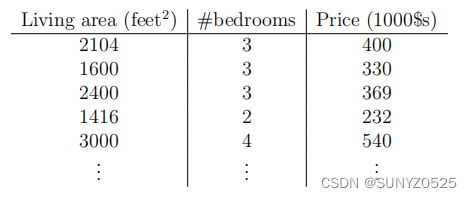
这里，$x$是${\mathbb{R}}^2$中的二维向量。例如，$x_1^{(i)}$是训练集中的第i个房子的居住区域，而$x_2^{(i)}$是它的卧室数量。（一般来说，当设计一个学习问题，它将由你决定选择什么功能，所以如果你在波特兰收集住房数据，你也可能决定包括其他功能，如每个房子是否有壁炉，浴室的数量，等等。我们稍后会说更多关于特性选择的内容，但现在让我们采用给定的特性。)
为了进行监督学习，我们必须决定如何在计算机中表示函数/hypotheses $h$。
作为一个初始选择，假设我们决定将$y$近似为$x$的线性函数：
$$h_{\theta (x)}={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2$$
在这里，${\theta }_i$的是参数（也称为权重）参数化的线性函数的空间从$\mathcal{X}$到$\mathcal{Y}$的映射。当没有混淆的风险时，我们将删除$h_{\theta }(x)$中的$\theta$下标，并将其更简单地写为$h(x)$。为了简化我们的公式，我们还引入了让$x_0=1$（这是截距项）的约定，这样
$$h(x)=\sum _{i=0}^n{\theta }_i{x}_i={\theta }^{T}x$$
在右边，我们把$\theta$和$x$都看作向量，这里$n$是输入变量的数量（不包括$x0$）。
现在，给定一个训练集，我们如何选择或学习参数$\theta$？一个合理的方法似乎是使$h(x)$接近$y$，至少在我们有的训练例子中是这样。为了使其形式化，我们将定义一个函数，它度量，对于$\theta$的每个值，$h(x^{(i)})$与相应的$y^{(i)}$的接近程度。我们定义了损失函数：
$$J(\theta )=\frac{1}{2}\sum _{i=1}^m{(h(x^{(i)})-y^{(i)})}^2$$
如果您以前见过线性回归，您可能会认为这是我们熟悉的最小二乘代价函数，它产生了普通最小二乘回归模型。

梯度下降算法

我们想选择$\theta$来最小化$J(\theta )$。为了做到这一点，让我们使用一个搜索算法，从θ的一些“初始猜测”开始，反复改变$\theta$，使$J(\theta )$更小，直到希望我们收敛到一个θ值，使最小化$J(\theta )$。

梯度下降算法的优化和改进包括批量梯度下降（Batch Gradient Descent）、随机梯度下降（Stochastic Gradient Descent）、小批量随机梯度下降（Mini-batch Stochastic Gradient Descent）、自适应学习率的梯度下降算法（AdaGrad、Adam、RMSProp）等。
批量梯度下降算法是每次使用全部的训练数据计算梯度，并进行参数更新。这种算法可以得到较为准确的梯度，但计算速度较慢，对于大规模数据集不太适用。
随机梯度下降算法是每次使用一个样本计算梯度，并进行参数更新。这种算法计算速度快，但容易受到样本噪声的影响，可能会出现震荡现象。
小批量随机梯度下降算法是在批量梯度下降和随机梯度下降之间的一种折中方法。每次使用一小部分样本计算梯度，并进行参数更新。这种算法兼具两种算法的优点，既可以得到较准确的梯度，又可以在一定程度上避免噪声的影响。
自适应学习率的梯度下降算法是根据梯度的历史信息自适应地调整学习率，可以更好地平衡学习速度和梯度方向的变化。这些算法通常使用一些平衡速度和方向变化的方法，例如使用指数加权移动平均（Exponential Weighted Moving Average）来估计梯度的方向和大小。
总的来说，梯度下降算法是机器学习中最基础和常用的优化算法之一，可以用于训练各种类型的模型，例如线性回归、逻辑回归、神经网络等。不同的梯度下降算法适用于不同的情况，选择适当的算法可以提高模型的训练效果和效率。

在详细讲解梯度算法之前，我们先了解梯度算法中的一些常见的重要概念。
预测函数（Prediction function）：在机器学习中，为了拟合样本而采用预测函数。例如线性回归表达式中$y=\omega x+b（{\omega }_i={\omega }_1,{\omega }_2\dots \dots {\omega }_N）$，Wi表示权重，$y$表示输出值，也成为预测值。而X表示输入值，也成为样本特征值。B在此处称为截距项，目的在于防止训练出的模型必定通过原点，提升了模型的适用范围。
损失函数（Loss function）：损失函数用于评估训练出的模型的拟合程度。损失函数越大，意味着模型拟合效果越差。在机器学习中，梯度下降法的根本目是在迭代中寻找损失函数的最小值，并通过反向传播的方式调整各个权重的大小，知道模型拟合程度达到指定要求。
步长（Learning rate）：步长决定了在梯度下降的过程中沿梯度负方向移动的距离，也就是对应于上文中所提到的两次测量最陡路径之间的距离，在机器学习中也被成为学习率。

具体来说，让我们考虑梯度下降算法，它从一些初始$\theta$开始，并反复执行更新：
$${\theta }_j={\theta }_j-\alpha \frac{\partial }{\partial \theta }J(\theta )$$
（这个更新是同时对$j=0,\dots \dots ,n$的所有值执行的）在这里，$\alpha$被称为学习率。这是一个非常自然的算法，它不断地朝着$j$最陡下降的方向迈出一步。
为了实现这个算法，我们必须计算出右边的偏导数项。让我们首先解决我们只有一个训练示例$(x,y)$，这样我们就可以忽略$j$定义中的和。我们有：
$$\begin{array}{c}\begin{array}{rl}\frac{\partial }{\partial \theta }J(\theta )& =\frac{\partial }{\partial \theta }\frac{1}{2}{(h_{\theta }(x)-y)}^2\\ & =2\cdot \frac{1}{2}(h_{\theta }(x)-y)\cdot \frac{\partial }{\partial \theta }(h_{\theta }(x)-y)\\ & =(h_{\theta }(x)-y)\cdot \frac{\partial }{\partial \theta }\left(\sum _{i=0}^n{\theta }_i{x}_i-y\right)\\ & =(h_{\theta }(x)-y)x_j\end{array}\end{array}$$
对于单个训练示例，这就给出了更新规则：
$${\theta }_j:={\theta }_j+\alpha (y^{(i)}-h_{\theta }(x^{(i)}))x_j^{(i)}$$
该规则被称为LMS更新规则（LMS代表“最小均方乘”）。这个规则有几个看起来很自然和直观的属性。例如，更新的大小与误差项$(y^{(i)}-h_{\theta }(x^{(i)}))$成正比；因此，如果我们遇到一个训练示例，我们的预测几乎匹配$y^{(i)}$的实际值，那么我们发现几乎不需要改变参数；相反，如果我们的预测$h_{\theta }(x^{(i)})$有很大的误差（即：离$y^{(i)}$非常远），参数将会发生更大的变化。
当只有一个训练示例时，我们推导出了LMS规则。对于包含多个例子的训练集，有两种方法来修改此方法。第一种是用以下算法替换它：
重复至收敛：
${\theta }_j:={\theta }_j+\alpha {\sum }_{i=1}^m(y^{(i)}-h_{\theta }(x^{(i)}))x_j^{(i)}$（for evert $j$）
注：我们使用符号“a：=b”来表示一个操作（在计算机程序中），其中我们将一个变量a的值设置为等于b的值。换句话说，此操作用b的值覆盖a。相反，当我们断言一个事实陈述时，我们会写一个=b，即a的值等于b的值。

可以很容易地验证上述更新规则中求和中的数量只是$\partial J(\theta )/\partial {\theta }_j$（对于$J$的原始定义）。因此，这只是原始成本函数$J$的梯度下降。此方法查看每个步骤的整个训练集中的每个示例，称为批量梯度下降。请注意，虽然梯度下降一般容易受到局部最小值的影响，但我们在这里提出的线性回归的优化问题只有一个全局，没有其他局部最优；因此梯度下降总是收敛（假设学习率$\alpha$不是太大）到全局最小值。事实上，$J$是一个凸二次函数。这里有一个梯度下降的例子，因为它是为了最小化二次函数而运行的。
有一种替代的批量梯度下降，也工作得非常好。请考虑以下算法：
Loop{
 for i=1 to m,{
  ${\theta }_j:={\theta }_j+\alpha (y^{(i)}-h_{\theta }(x^{(i)}))x_j^{(i)}$ （for evert $j$）
 }
}
在该算法中，我们反复运行训练集，每次遇到训练例时，我们只根据相对于单个训练例的误差梯度更新参数。这种算法被称为随机梯度下降（也称为增量梯度下降）。而批处理梯度下降必须在采取一步之前扫描整个训练集——如果m很大，这是一个昂贵的操作——随机梯度下降可以立即开始取得进展，并在它所看到的每个例子中继续取得进展。通常，随机梯度下降使$\theta$“接近”最小值快得多。(但是请注意，它可能永远不会“收敛”到最小值，而参数$\theta$ 将保持在$J(\theta )$的最小值附近振荡；但在实践中，大多数接近最小值的值将是相当好的接近真正的最小值。2)由于这些原因，特别是当训练集很大时，随机梯度下降往往比批量梯度下降更可取。
虽然更常见的运行随机梯度下降，我们描述了一个固定的学习速率α，通过慢慢让学习率α下降到零算法运行，也可以确保参数将收敛到全球最小而不振荡最低。

感知器算法

感知器算法：BP算法的思想基础
输入——计算——输出
输入：不同的参数有不同的权重
计算：求和——激活
输出：可以有多个

一般用向量来表示
输入（$x$）： { x 0 , x 1 , … … , x m } \{x_0,x_1,……,x_m\} {x0​,x1​,……,xm​}
权重（$\omega$）： { ω 1 , ω 2 , … … , ω 3 } \left\{\omega_1,\omega_2,……,\omega_3 \right\} {ω1​,ω2​,……,ω3​}
求和（$\Sigma$）
激活（$\sigma$）：导数、激活率
输出（$y$）：$y=\sigma ({\omega }^{T}x)$

感知器算法：
$y=\sigma ({\omega }^{T}x)$=>$h(\theta )={\omega }^T\theta$
$$\theta =\theta -\partial {\nabla }_{\theta }\text{\hspace{1em}(1)}$$
对于单一用例 ：$\nabla {\theta }_i=(h(\theta )-y_i)x_i$
=>BP算法
初始化： $\omega$
重复至收敛：式（1）