SkipList 跳表-优快云博客

本文链接：https://blog.youkuaiyun.com/qq_51086532/article/details/137246983

本文介绍了跳表的数据结构原理，包括其查询、增加和删除操作的逻辑，以及在GO语言中的实现。作者通过实例展示了如何在跳表中高效查询并演示了插入和删除的步骤，同时分享了学习跳表在研究生阶段时间碎片化环境下的心得体会。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

文章目录

查询
增加
删除
写法优化 GO版本
题外话

最近在读 LevelDB 的源码，正好看到里面使用了跳表这种数据结构于是学习一下

跳表实际上是由多个链表组成的，时间复杂度是O(logn)

一种思路：

每相邻两个节点升高一层，增加一个指针，让指针指向下一个节点
以此类推，我们可以在第二层新产生的链表上，继续为每相邻的两个节点升高一层
如果严格按照上面的设计来执行，那么调表的查询的时间复杂度时logN，但是插入和删除结构不太好，因为需要大范围的调整结构，来维护规则二。

上面所述的规则如果严格执行，查询的效率会很高，但是插入和删除会十分麻烦，所以跳表采用概率在尽量不增加时间复杂度的同时，更加容易插入和删除

整个跳表会有一个节点的最大高度maxlevel，跳表所有节点的高度都不会超过这个maxlevel
跳表会维护一个头节点，头结点后面都是插入的数据
跳表以null ，作为链表的终点

下边是一个跳表的简单结构，节点的定义如下:

class Node {
public:
    // 这个maxlevel  是 跳表的最大层数，我们这边先把空间开辟好，防止扩容造成不必要的拷贝
    Node(int v = -1, int maxlevel = 0) :val(v) {
        next.reserve(maxlevel);
    }
    int val;  // 节点存储的值
    vector<Node*> next;  // 当前节点的层数
};

那么一个节点的有几层该如何确定呢？这就是跳表的精髓，首先我们有一个概率p，这个p代表有多大几率节点层数+1，请看下面的一段伪代码，v代表节点的层数，maxlevel 是跳表的最大层数，rand 是[0,1]的随机值

int v=1;
while(v< maxlevel &&  rand()< p){
    v++;
}

按照上面的代码我们可以随机的取到每一个新节点的层数，如果数据量足够大的时候，每一次的概率理论上应该为：

层数	概率
1层	1-p
2层	p*(1-p)
3层	p^2*(1-p)

后面以此类推就不在列举了，所以如果数据量为N（数据量足够大），那么每一层的数量就是概率*N，假设在这里的p==0.5，我们就可以推出一层大概有二分之一的数据、二层大概有四分之一的数据… 至于为什么这样做的时间复杂度为log(N)就不在我们的讨论范围之内，有兴趣的可以自己查一查论文。

下面就是跳表的实现部分，这里我是按照 leetcode 上的一道题目来完成的，这道题就是让我们设计一个跳表，最后还有测试用例，这就很舒服，可以验证我们的跳表的正确性

查询

如何在跳表中查询一个元素？这个十分简单，总结下来就是下面几个规则：

如果查询的值比当前层下一个节点大向右走
如果查询的值比当前层下一个节点要小 || 当前层下一个节点为NULL 向下走
查询都是当前节点的最大层数向下查询
当层数小于0 的时候就应该跳出循环了

以下面这个跳表为例：我们要查询元素7

下面查询的所有画图 9 号节点应该有一个箭头指向null ，我是画完才发现的，☝这个是正确的，但是并不影响查询的逻辑我就不改了哈😋

首先我们从头结点的最大层出发，首先我们判断出，下一个几点为null，所以要查询的节点一定在第三层的下面的层数的链表中

来到头结点的第二层，我们发现第二层的下一个几点9 比我们要查询的7 要大，所以按照规则继续向下走

这时我们来到了头结点的第一层，我们发现下一个节点比 7 小，按照规则我们应该向右边走

7 比当前节点在第一层的下一个节点要小，所以向下走！

最后我们在来到了当前节点的的第0层，发现下一个节点就是我们要找的7，所以直接返回找到

所以查询的代码如下：
如果对判断条件 curLevel >= 0不太理解的读者，可以带入一个跳表中不存在的值，再走一下流程就能理解了！

class Node {
public:
    Node(int v = -1, int maxlevel = 0) :val(v) {
        next.reserve(maxlevel);
    }
    int val;
    vector<Node*> next;
};


class Skiplist {
public:
    Skiplist() :head(-1, maxlevel) {
        head.next.resize(maxlevel);
    }
    // next 比target 大向下走
    // next 比target小 向右走
    bool search(int target) {
        Node* cur = &head;
        int curLevel = head.next.size()-1;
        // 如果查询的层出小于0 代表找不到
        while (curLevel >= 0) {
            if (cur->next[curLevel] == nullptr || cur->next[curLevel]->val > target) {
                curLevel--;
            }
            else if (cur->next[curLevel]->val < target) {
                cur = cur->next[curLevel];
            }
            else // cur.next[curLevel]->val == target
                return true;
        }
        // 如果走到这里 都没有return 那么代表 跳表中不存在target 直接返回false
        return false;
    }

private:
    double p=0.5;
    //std::default_random_engine e;
    int maxlevel = 4;
    Node head;
};

增加

增加和删除是一个思路，所以这里我们重点介绍一下插入的思路：
因为按照leetcode 题目的意思我们是可以插入重复的元素，所以我们要在当前跳表中插入元素12，先不介绍如何插入一个节点，我们观察一下下面的链表，我们认为 12 这个节点有两个插入的位置

这里我写的这个版本是在位置2 插入的，最后给的那一版GO语言的版本是在位置1 插入的！大伙可以对比着看一下👀
我们发现如果我们要插入一个节点，我们得找到两个东西：

首先就是上图椭圆的位置，只有找到这个位置才能知道在哪里插入
其次就是找到插入位置，每一层对应的上一个节点见下图的绿色的节点👇

这些节点我们可以在上面的查找过程中用一个数组（数组的长度等于）记录下来，记录这个节点的规则也十分简单只有一条：
向下走之前把当前节点记录下来，记录到对应层的数组位置上！

我们首先创建一个大小和跳表 maxlevel 层数相同的 pre 数组用来记录位置2 的每一层的前一个节点

首先我们还是从头结点的最高层开始，发现当前层的下一个节点是空，应该向下走，并将该节点入到数组的入到pre 数组的第三层

这时候我们发现当前层的下一个节点的值比插入的值要小应该向右走

这时候按照规则判断应该向下走，并且记录到pre 数组的对应位置上，

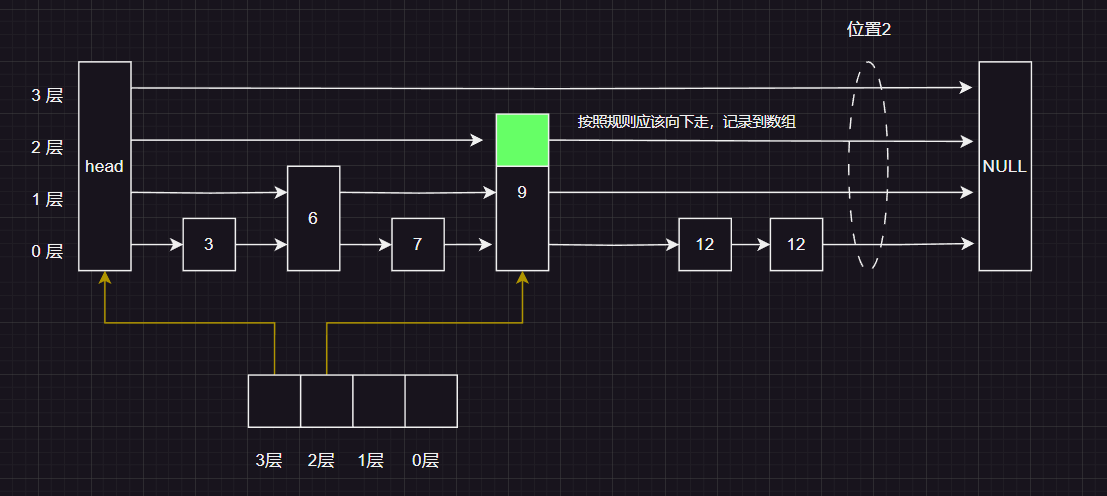
按照规则应该向下走，并且记录到pre 数组对应的位置上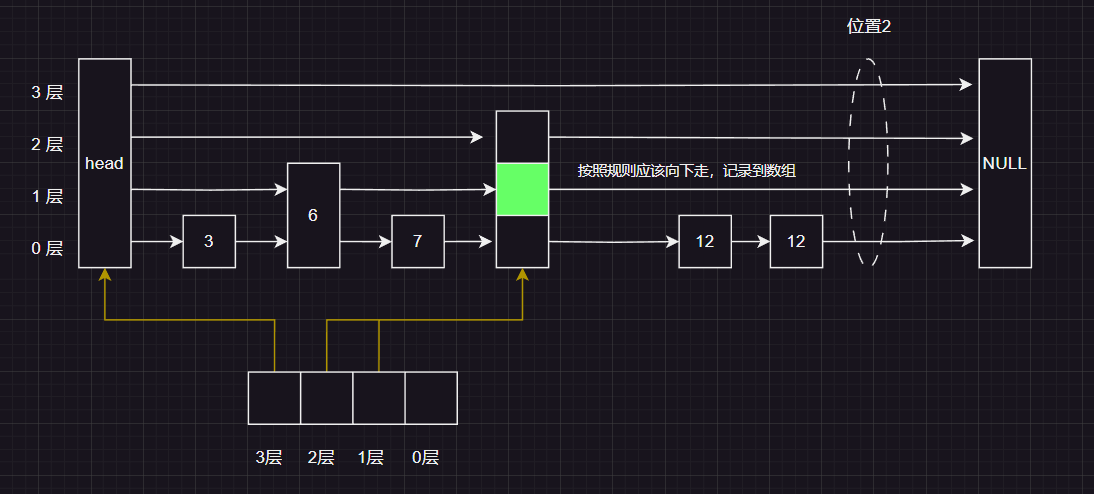

这时候我们发现下一个节点等于我们要插入的值，现在有两种选择：

如果相当向右走，那么最终插入的位置是位置2
如果向下走，那么最终插入的位置是位置1

这里我们选择继续向右走，插入位置2

走到这里， level 减到-1 ，直接跳出循环，我们也找到了插入的位置和该位置对应所有层的前置节点。接下来就是：

确定插入节点的层数
插入节点

如何确定插入节点的层数我们上面已经介绍过了，这里直接贴一个实现：
注意 RAND_MAX 是一个宏，rand函数取的值不会超过这个宏定义的值

  int RandomLevel() {
        int v=1;
        while(v< maxlevel &&  rand()< RAND_MAX * p){
            v++;
        }
        return v;
    }

接下来就是简单的链表插入，但是注意需要把新节点的所有层数都插入到对应层链表里面

下面示例的是如果随机的值是两层，那么最终插入的结果就是：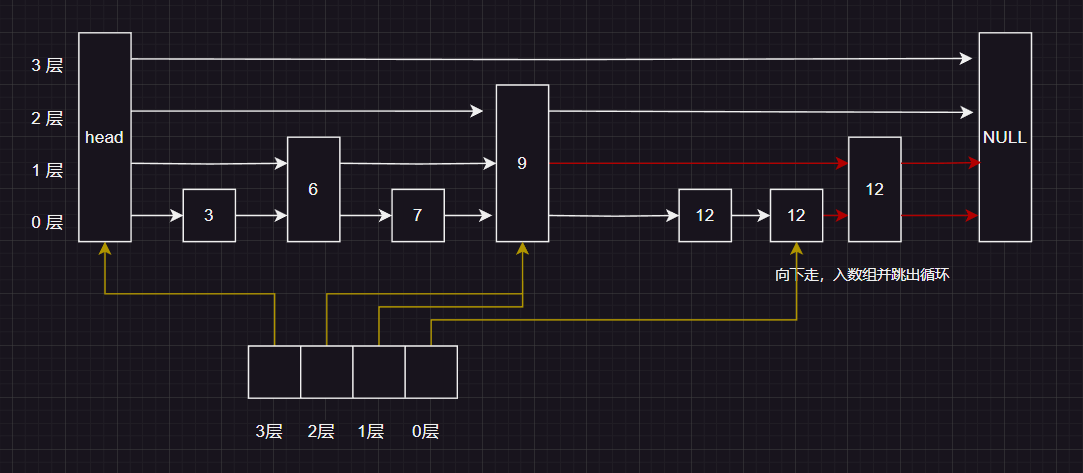

到这里一个简单的跳表插入就已经完成了代码如下👇

class Node {
public:
    Node(int v = -1, int maxlevel = 0) :val(v) {
        next.reserve(maxlevel);
    }
    int val;
    vector<Node*> next;
};


class Skiplist {
public:
    Skiplist() :head(-1, maxlevel) {
        head.next.resize(maxlevel);
        //srand(time(0));
    }
    int RandomLevel() {
        int v=1;
        while(v< maxlevel &&  rand()< RAND_MAX * p){
            v++;
        }
        //cout<<v+1<<endl;
        return v;
    }

    void add(int num) {
        vector<Node*> pre(maxlevel);
        Node* cur = &head;
        int curLevel = head.next.size()-1;
        while (curLevel >= 0) {
            if (cur->next[curLevel] == nullptr || cur->next[curLevel]->val > num) {
                pre[curLevel] = cur;
                curLevel--;
            }
            else if (cur->next[curLevel]->val < num) {
                cur = cur->next[curLevel];
            }else{
                cur = cur->next[curLevel];
                pre[curLevel] = cur;
                curLevel--;
            }
        }

        int rlevel = RandomLevel();
        Node* newnode = new Node(num, maxlevel);
        newnode->next.resize(rlevel);
        for (int i = 0; i < rlevel; i++) {
            newnode->next[i] = pre[i]->next[i];
            pre[i]->next[i] = newnode;
        }
    }
private:
    double p=0.5;
    //std::default_random_engine e;
    int maxlevel = 4;
    Node head;
};

删除

删除的逻辑和插入是一模一样的，这里就不详细介绍了说一下思路：

找到删除的节点的位置，如果没有找到直接返回
在查找删除节点的过程中记录删除位置对应每一层的前一个节点，得到一个pre 数组
最后就是更具删除节点的层数，对每一层的pre 数组做一个简单的链表删除！

实际上只有最后一步和插入不一样，插入的最后一步是一个链表的插入，删除的最后一步是一个链表的删除😂

写法优化 GO版本

对于上面的代码过于冗余，查询、删除、增加都有部分逻辑是公共的，可以提取出来放在一个公用的函数用来调用，但是非常适合初学者想明白逻辑，所以我前面讲解的时候使用的就是冗余的代码，下面给出一个Go语言版本的跳表，这个版本的把所有的公共逻辑都放到了Find函数中。

type Node struct {
    Val  int
    Next []*Node
}

func CreateNode(val, level int) *Node {
    cur := new(Node)
    cur.Val = val
    cur.Next = make([]*Node, 0, level)
    return cur
}

type Skiplist struct {
    maxlevel int
    p        float32
    Node
}

func Constructor() Skiplist {
    var sk Skiplist
    sk.maxlevel = 8
    sk.p = 0.5
    sk.Next = make([]*Node, 8) // 头结点的高度直接设置为8
    sk.Val = -1
    return sk
}

// 返回值 bool 有没有target 这个节点
// 返回值 []*Node 代表每一层的前一个节点的数组
func (this *Skiplist) Find(target int) (bool, []*Node) {

    pre := make([]*Node, this.maxlevel)
    flag := false
    cur := &(this.Node)
    curlevel := this.maxlevel - 1
    for curlevel >= 0 {
        if cur.Next[curlevel] == nil || cur.Next[curlevel].Val > target {
            // 向下走
            pre[curlevel] = cur
            curlevel--
        } else if cur.Next[curlevel].Val < target {
            // 向右走
            cur = cur.Next[curlevel]
        } else {
            flag = true
            pre[curlevel] = cur
            curlevel--
        }
    }
    if flag {
        return true, pre
    }
    return false, pre

}

func (this *Skiplist) RabdomLevel() int {

    rand.Intn(10000)
    v := 1
    for v < this.maxlevel && rand.Intn(10000) < int(float32(10000)*this.p) {
        v++
    }
    return v
}

func (this *Skiplist) Search(target int) bool {
    ret, _ := this.Find(target)
    return ret
}

func (this *Skiplist) Add(num int) {
    _, pre := this.Find(num)

    l := this.RabdomLevel() // 新节点的 高度

    newnode := CreateNode(num, this.maxlevel)
    newnode.Val = num

    for i := 0; i < l; i++ {
        tmp := pre[i].Next[i]
        pre[i].Next[i] = newnode
        newnode.Next = append(newnode.Next, tmp)
    }
}

func (this *Skiplist) Erase(num int) bool {
    ret, pre := this.Find(num)
    if ret == false {
        return false
    }

    cur := pre[0].Next[0]
    for i := 0; i < len(cur.Next); i++ {
        pre[i].Next[i] = pre[i].Next[i].Next[i]
    }
    return true
}

题外话

上了研究生之后，我们组导师有点压榨，很难抽出大把的时间来学习，现在的学习时间都十分零碎，可能上午半个小时，下午活干完了有半个小时的空余时间。以前我都是一整个下午或一整个上午用来学习。这弄得我十分难受，在这里吐槽一下，这也倒逼我开始改变策略，如果想要进步那就要抓紧这些零碎的时间利用起来。以前我十分瞧不起这种零碎的时间，因为进度很小没有啥成就感，但是坚持了一段时间我发现实际学习进度也是在缓步推进的，于是我得出一个结论： 重点不是每天学习进度的多少，重点是每天都在坚持的去做、去学习 每天都持之以恒的做不管每天能推进多少）实际上是最重要的（因为现在确实很难平衡工作和学习，时间是真的不够用啊😭），实际上一段时间下来还是能积累下来很多东西的。
希望对你有帮助。