数组算法讲解

于 2023-11-12 20:42:26 发布
阅读量72 收藏
点赞数
文章标签： 算法 c++ leetcode
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/qq_51065805/article/details/134290395
版权

一：数据基础概念

1.1 一维数组

1.2 二位数组

二：双指针解数组

2.1 快慢指针技巧

快慢指针主要解决的问题：让你原地修改数组

2.1.1力扣第 26 题「删除有序数组中的重复项」

思路：快慢指针，slow 用于存储 fast 用于判断
在这里插入图片描述

class Solution {
public:
    int removeDuplicates(vector<int>& nums) {
        int dex = 1;
        for( int slow = 0,fast = 1;fast<nums.size();fast++ )
        {

            if(nums[slow]  != nums[fast])
            {
                dex++;
                slow++;
                nums[slow] = nums[fast];
            }
        }
        return dex;
    }
};
2.1.2 额外扩充，去除链表重复值呢，力扣第 83 题「删除排序链表中的重复元素」

此处直接递归法做的：

class Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        if(head == nullptr || head->next == nullptr)
        {
            return head;
        }
        head->next = deleteDuplicates(head->next);
        return head->val == head->next->val ? head->next : head;
    }
};

遍历也可以，代码如下：

lass Solution {
public:
    ListNode* deleteDuplicates(ListNode* head) {
        if(head == nullptr)
        {
            return head;
        }
        ListNode* slow = head;
        ListNode* fast = head->next;
        while(fast != nullptr)
        {
            if(fast->val != slow->val)
            {
                slow->next = fast;
                slow = slow->next;
                
            }
            fast = fast->next;
        }
        slow->next = nullptr;
        return head;
    }
};
2.1.3 力扣第 283 题「https://leetcode.cn/problems/move-zeroes/」：

熟悉上文原地修改方法，我们给出代码：
其中，我注释掉的代码，也为一种方法，属于是 0 和非0值交换位置，这样也可以让 0 全部放在末尾。

class Solution {
public:
    void moveZeroes(vector<int>& nums) {
        // int size = nums.size();
        // int left = 0,right = 0;
        // while(right<size)
        // {
        //     if(nums[right])
        //     {
        //         swap(nums[left],nums[right]);
        //         left++;
        //     }
        //     right++;
        // }

        int p = removezore(nums,0);
        for(int i = p; i<nums.size();i++)
        {
            nums[i] = 0;
        }
    }
    int removezore(vector<int> &nums,int n)
    {
        int fast = 0;
        int slow = 0;
        while(fast<nums.size())
        {
            if(nums[fast] != n)
            {
                nums[slow] = nums[fast];
                slow++;
            }
            fast++;
        }
        return slow;
    }
};

2.2 左右指针常用算法

2.2.1 二分查找

二分查找，一左一右相向而行
代码模板：

int binarySearch(vector<int>& nums, int target) {
    // 一左一右两个指针相向而行
    int left = 0, right = nums.size() - 1;
    while(left <= right) {
        int mid = (right + left) / 2;
        if(nums[mid] == target)
            return mid; 
        else if (nums[mid] < target)
            left = mid + 1; 
        else if (nums[mid] > target)
            right = mid - 1;
    }
    return -1;
}
2.2.2 两数之和问题

力扣第 167 题「两数之和 II」：

class Solution {
public:
    vector<int> twoSum(vector<int>& numbers, int target) {
        int slow = 0;
        int fast = numbers.size() - 1;
        while(slow < fast)
        {
            int sum = numbers[slow] + numbers[fast];
            if(sum == target)
            {
                return {slow+1,fast+1};
            }
            if(sum < target)
            {
                slow++;
            }
            if(sum > target)
            {
                fast--;
            }
        }
        return {};
    }
};
2.2.3 反转数组

力扣第 344 题「反转字符串」
方法一：利用上文讲解方法，双指针，一左一右，相互交换

class Solution {
public:
    void reverseString(vector<char>& s) {
        
        int left = 0;
        int right = s.size()-1;
        while(left < right)
        {
            char temp = s[left];
            s[left] = s[right];
            s[right] = temp;
            left++;
            right--;
        }
    }
};

方法二：直接调用 reverse 函数

        reverse(s.begin(),s.end());
2.24 回文串判断

上一篇链表也阐述过回文问题，双指针做法，此处思路也基本一样
模板代码：

bool isPalindrome(string s) {
    // 一左一右两个指针相向而行
    int left = 0, right = s.length() - 1;
    while (left < right) {
        if (s[left] != s[right]) { // 如果不相同，就不是回文串
            return false;
        }
        left++;
        right--;
    }
    return true;
}

力扣第 5 题「最长回文子串」
在链表问题我们写过下面代码：
如果 l 和 r 相同，则我们得到的是长度为奇数的回文串
如果 l 和 r 相邻，则我们得到的是长度为偶数的回文串

// 在 s 中寻找以 s[l] 和 s[r] 为中心的最长回文串
string palindrome(string s, int l, int r) {
    // 防止索引越界
    while (l >= 0 && r < s.length()
            && s[l] == s[r]) {
        // 双指针，向两边展开
        l--; r++;
    }
    // 返回以 s[l] 和 s[r] 为中心的最长回文串
    return s.substr(l + 1, r - l - 1);
}

意义就是找寻以 s[l] 和 s[r] 为中心的最大回文串。
对于这道题呢，我们就调用该函数，遍历，直到找打最大的。

class Solution {
public:
    string longestPalindrome(string s) {
        string result = "";
        for(int i = 0; i< s.length();i++)
        {
            string s1 = palidrome(s,i,i);
            string s2 = palidrome(s,i,i+1);
            result = result.length() > s1.length() ? result : s1;
            result = result.length() > s2.length() ? result : s2;
        }
        return result;
    }

    string palidrome(string s, int l, int r)
    {
        while(l>=0 && r<s.length()&&s[l] == s[r])
        {
            l--;
            r++;
        }
        return s.substr(l+1,r-l-1);
    }
};

三：算法技巧：前缀和数组

3.1 一维数组中前缀和

力扣第 303 题「区域和检索 - 数组不可变」
思路一：在计算和的函数中 for 循环进行累加

class NumArray {
public:
    vector<int> res;

    NumArray(vector<int>& nums) {
        res = nums;
    }
    
    int sumRange(int left, int right) {
        int sum  = 0;
        while(left<=right)
        {
            sum += res[left];
            left++;
        }
        return sum;
    }
};

思路二： 优化 sumRange 空间复杂度
在这里插入图片描述

class NumArray {
    private:
        // 前缀和数组
        vector<int> preSum;
    
    public:
        /* 输入一个数组，构造前缀和 */
        NumArray(vector<int>& nums) {
            // preSum[0] = 0，便于计算累加和
            preSum.resize(nums.size() + 1);
            // 计算 nums 的累加和
            for (int i = 1; i < preSum.size(); i++) {
                preSum[i] = preSum[i - 1] + nums[i - 1];
            }
        }
        
        /* 查询闭区间 [left, right] 的累加和 */
        int sumRange(int left, int right) {
            return preSum[right + 1] - preSum[left];
        }
};

3.2 二位矩阵中的前缀和

力扣第 304 题「二维区域和检索 - 矩阵不可变」
思路：和一维矩阵是类似的，我们重新定义的二维矩阵是原矩阵的累计和。
在这里插入图片描述

class NumMatrix {
public:
    vector<vector<int>> result;

    NumMatrix(vector<vector<int>>& matrix) {
        int x = matrix.size();
        int y = matrix[0].size();
        if(x== 0 || y == 0)
        {
            return ;
        }
        result = vector<vector<int>>(x + 1, vector<int>(y + 1));
        for(int i = 1 ; i <= x ; i++)
        {
            for(int j = 1; j <= y;j++)
            {
                result[i][j] = result[i-1][j] + result[i][j-1] + matrix[i-1][j-1] - result[i-1][j-1]; 

            }
        }
    }
    
    int sumRegion(int row1, int col1, int row2, int col2) {
        return result[row2+1][col2+1] - result[row2+1][col1+1] - result[row1+1][col2+1] + result[row1+1][col1+1];
    }
};

四： 算法技巧：差分数组

4.1差分方程原理和代码模板：

差分数组主要用于频繁对原始数组的某个区间元素进行增减
构造差分数组：

int diff[nums.size()];
// 构造差分数组
diff[0] = nums[0];
for (int i = 1; i < nums.size(); i++) {
    diff[i] = nums[i] - nums[i - 1];
}

在这里插入图片描述
对原始数组，我们可以通过 diff 差分数组进行反推：

int res[diff.size()];
// 根据差分数组构造结果数组
res[0] = diff[0];
for (int i = 1; i < diff.size(); i++) {
    res[i] = res[i - 1] + diff[i];
}

这样的意义：构造差分数组 diff，就可以快速进行区间增减的操作，比如对区间 nums[i…j] 的元素全部加 3，那么只需要让 diff[i] += 3，然后再让 diff[j+1] -= 3 即可：
在这里插入图片描述
对于差分数组问题，我们直接给出了一个 class 模板，里面包括修改函数和返回函数：

// 差分数组工具类
    class Difference {
    private: 
        vector<int> diff;

    public:
        Difference(const vector<int>& nums) {
            int length = nums.size();
            assert(length > 0);
            diff.resize(length);
            diff[0] = nums[0];
            for (int i = 1; i < length; i++) {
                diff[i] = nums[i] - nums[i - 1];
            }
        }

        void increment(int i, int j, int val) {
            diff[i] += val;
            if (j + 1 < diff.size()) {
                diff[j + 1] -= val;
            }
        }

        vector<int> result() {
            vector<int> res(diff.size(), 0);
            res[0] = diff[0];
            for (int i = 1; i < res.size(); i++) {
                res[i] = res[i - 1] + diff[i];
            }
            return res;
        }
    };

对于上文函数 increment
这个判断的意义是，当 j+1 >= diff.length() ,代表是对 i 之后的整个数组都进行修改，就不需要再给后面减掉 val 值了。

 if (j + 1 < sizeof(diff) / sizeof(diff[0]))

4.2 差分方程强化试练：

力扣第 1109 题「航班预订统计」：
下文我们是直接使用上文写出的 class 类的差分模板

class Solution {
public:
    class Difference {
    private: 
        vector<int> diff;

    public:
        Difference(const vector<int>& nums) {
            int length = nums.size();
            assert(length > 0);
            diff.resize(length);
            diff[0] = nums[0];
            for (int i = 1; i < length; i++) {
                diff[i] = nums[i] - nums[i - 1];
            }
        }

        void increment(int i, int j, int val) {
            diff[i] += val;
            if (j + 1 < diff.size()) {
                diff[j + 1] -= val;
            }
        }

        vector<int> result() {
            vector<int> res(diff.size(), 0);
            res[0] = diff[0];
            for (int i = 1; i < res.size(); i++) {
                res[i] = res[i - 1] + diff[i];
            }
            return res;
        }
    };

    vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {
        vector<int> nums(n, 0);
        Difference diff(nums);
        for (const auto& book : bookings) {
            int i = book[0] - 1;
            int j = book[1] - 1;
            int val = book[2]; 
            diff.increment(i, j, val);
        }
        return diff.result();
    }
};

下文代码，我们不再专门写差分 class 类

class Solution {
private : 
    vector<int> diff;
    int length;
public:
    vector<int> corpFlightBookings(vector<vector<int>>& bookings, int n) {
        diff.resize(n,0);
        length = n;
        for(auto& book:bookings)
        {
            int i = book[0] - 1;
            int j = book[1] - 1;
            int val = book[2];
            increment(i,j,val);
        }
        // 下面for 是差分累计差分数组还原原数组 
        for(int i = 1 ;i<length;i++)
        {
            diff[i] += diff[i-1];
        }
        return diff;
    }
    // 这步是差分数组 
    void increment(int i,int j, int val)
    {
        diff[i] +=val;
        if(j + 1 < length)
        {
            diff[j + 1] -= val;
        }
    }
};

我们额外再加一道题：力扣第 1094 题「拼车」
下文方法依旧是参考的上文模板，不是很熟练，可以适当再手写加强一下。

// class Solution {
//     class Difference {
//     private: 
//         vector<int> diff;

//     public:
//         Difference(const vector<int>& nums) {
//             int length = nums.size();
//             assert(length > 0);
//             diff.resize(length);
//             diff[0] = nums[0];
//             for (int i = 1; i < length; i++) {
//                 diff[i] = nums[i] - nums[i - 1];
//             }
//         }

//         void increment(int i, int j, int val) {
//             diff[i] += val;
//             if (j + 1 < diff.size()) {
//                 diff[j + 1] -= val;
//             }
//         }

//         vector<int> result() {
//             vector<int> res(diff.size(), 0);
//             res[0] = diff[0];
//             for (int i = 1; i < res.size(); i++) {
//                 res[i] = res[i - 1] + diff[i];
//             }
//             return res;
//         }
//     };
// public:
//     bool carPooling(vector<vector<int>>& trips, int capacity) {
//         vector<int>nums(1001,0);
//         vector<int >result;
//         Difference diff(nums);
//         for(auto &tip:trips)
//         {
//             int val = tip[0];
//             int i = tip[1] ;
//             int j = tip[2] - 1;
//             diff.increment(i,j,val); 
//         }
//         result = diff.result();
//         for(int i = 0;i<1001;i++)
//         {
//             if(result[i]>capacity)
//             {
//                 return false;
//             }
//         }
//         return true;
//     }
// };


class Solution {
private:
    vector<int>diff;
    int length;

public:
    bool carPooling(vector<vector<int>>& trips, int capacity) {
        diff.resize(1001,0);
        length = 1001;
        for(auto &tip:trips)
        {
            int val = tip[0];
            int i = tip[1] ;
            int j = tip[2] - 1;
            increment(i,j,val); 
        }
        for(int i = 1; i<length;i++)
        {
            diff[i] += diff[i-1];
            cout<<diff[i]<<endl;
        }
        for(int i = 0;i<length;i++)
        {
            if(diff[i]>capacity)
            {
                return false;
            }
        }
        return true;
    }
    void increment(int i,int j ,int val)
    {
        diff[i] += val;
        if(j+1 <length)
        {
            diff[j+1] -= val;
        }
    }
};

4.3 差分方程代码总结：

最后总结一下，上文模板依然可以适当简化，不用专门写函数进行差分方程：

class Solution {
public:
    bool carPooling(vector<vector<int>> &trips, int capacity) {
       vector<int>result(1001,0);
       for(auto &tip:trips)
       {
           int val = tip[0];
           int i = tip[1];
           int j = tip[2];
           result[i] += val;
           result[j] -= val;
       }
       int s= 0;
       for(auto v:result)
       {
           s += v;
           if(s>capacity)
           {
               return false;
           }
       }
        return true; 
    }
};

在这个代码中：
这个地方我就直接进行了差分方程，这样大大简化了代码运行量，不过从入门角度来讲，上文的class 类更加方便易懂。

       for(auto &tip:trips)
       {
           int val = tip[0];
           int i = tip[1];
           int j = tip[2];
           result[i] += val;
           result[j] -= val;
       }

五： 二维数组的遍历技巧

5.1 顺/逆时针旋转矩阵

数组旋转问题，力扣第 48 题「旋转图像」
思路1：（假如不需要再原地修改数组）：我们重新创建个二维数组，经进行两个 for 遍历，如下大概模板

    vector<vector<int>> rotate(vector<vector<int>>& matrix) {
        vector<vector<int>>result;
        int x = matrix.size();
        int y = matrix[0].size();
        for(int i = 0;i<x;i++)
        {
            for(int j = 0;j<y;j++)
            {
            }
        }
    }

思路2：
1.我们现根据对角线进行对称
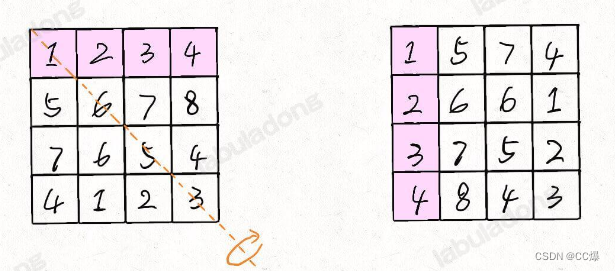
在这里插入图片描述
2.再每一行反转
在这里插入图片描述
3.总体观看：就是 matrix 顺时针旋转 90 度的结果：
在这里插入图片描述

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        // 对角线对称
        for(int i = 0;i<n;i++)
        {
            for(int j = i; j<n ; j++)
            {
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
        }
        // 数组反转
        for(auto &row:matrix)
        {
            reverse(row.begin(),row.end());
        }

    }
};

此处代码我的反转直接使用的库函数 reverse，如果需要自己定义函数如下：

    void reverse(vector<int>res)
    {
        //双指针，一前一后
        int i = 0;
        int j = rse.size() - 1;
        while(j>i)
        {
            int temp = res[i];
            res[i] = res[j];
            res[j] = temp;
            j--;
            i++;
        }
    }

总的来说，上文都是阐述的顺时针，那么逆时针也和顺基本一致：
在这里插入图片描述

5.2 矩阵螺旋遍历

力扣第 54 题「螺旋矩阵」
思路：就是右、下、左、上，顺时针旋转。
在这里插入图片描述

class Solution {
public:
    vector<int> spiralOrder(vector<vector<int>>& matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        int up = 0, right = n-1, left = 0, low = m-1;
        vector<int>res;
        while(res.size() < m*n)
        {
            //从左往右进行加入数据
            if(up <= low)
            {
                for(int j = left;j<=right;j++ )
                {
                    res.push_back(matrix[up][j]);
                }
                //上边界下移
                up++;
            }

            //从上往下加入数据
            if(left <= right)
            {
                for(int j = up ; j <= low ; j++)
                {
                    res.push_back(matrix[j][right]);
                }
                right--;
            }

            //从右往左加入数据
            if(up <= low)
            {
                for(int j =right ; j >= left ; j--)
                {
                    res.push_back(matrix[low][j]);
                }
                low--;
            }

            //从下往上加数据
            if(left <= right)
            {
                for(int j=low ; j>=up; j--)
                {
                    res.push_back(matrix[j][left]);
                }
                left++;
            }
        }
        return res;
    }
};

上文题为顺时针的螺旋遍历，接下来，力扣第 59 题「螺旋矩阵 II」，该题，刚好和上文反过来，属于是往二维里添加数据

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> matrix(n, vector<int>(n, 0));
        //int m = matrix.size();
        //int n = matrix[0].size();
        int up = 0, right = n-1, left = 0, low = n-1;
        int num = 1;
        // vector<int>res;
        while(num <= n*n)
        {
            //从左往右进行加入数据
            if(up <= low)
            {
                for(int j = left;j<=right;j++ )
                {
                    matrix[up][j] = num++;
                    //res.push_back(matrix[up][j]);
                }
                //上边界下移
                up++;
            }

            //从上往下加入数据
            if(left <= right)
            {
                for(int j = up ; j <= low ; j++)
                {
                    matrix[j][right] = num++;
                    //res.push_back(matrix[j][right]);
                }
                right--;
            }

            //从右往左加入数据
            if(up <= low)
            {
                for(int j =right ; j >= left ; j--)
                {
                    matrix[low][j] = num++;
                    //res.push_back(matrix[low][j]);
                }
                low--;
            }

            //从下往上加数据
            if(left <= right)
            {
                for(int j=low ; j>=up; j--)
                {
                    matrix[j][left] = num++;
                    //res.push_back(matrix[j][left]);
                }
                left++;
            }
        }
        return matrix;
    }
};

六： 滑动窗口问题

6.1 概念

滑动窗口本质问题就是双指针问题，大体模板如下：

/* 滑动窗口算法框架 */
void slidingWindow(string s) {
    // 用合适的数据结构记录窗口中的数据
    unordered_map<char, int> window;
    
    int left = 0, right = 0;
    while (right < s.size()) {
        // c 是将移入窗口的字符
        char c = s[right];
        window.add(c)
        // 增大窗口
        right++;
        // 进行窗口内数据的一系列更新
        ...

        /*** debug 输出的位置 ***/
        // 注意在最终的解法代码中不要 print
        // 因为 IO 操作很耗时，可能导致超时
        printf("window: [%d, %d)\n", left, right);
        /********************/
        
        // 判断左侧窗口是否要收缩
        while (left < right && window needs shrink) {
            // d 是将移出窗口的字符
            char d = s[left];
            window.remove(d)
            // 缩小窗口
            left++;
            // 进行窗口内数据的一系列更新
            ...
        }
    }
}

6.2 最小覆盖子串

力扣第 76 题「最小覆盖子串」
思路：

  1. 在字符串 S 中使用双指针中的左右指针技巧，初始化 left = right = 0，把索引左闭右开区间 [left, right) 称为一个「窗口」。
  2. 不断地增加 right 指针扩大窗口 [left, right)，直到窗口中的字符串符合要求（包含了 T 中的所有字符）。
  3. 此时，我们停止增加 right，转而不断增加 left 指针缩小窗口 [left, right)，直到窗口中的字符串不再符合要求（不包含 T 中的所有字符了）。同时，每次增加 left，我们都要更新一轮结果。
  4. 重复第 2 和第 3 步，直到 right 到达字符串 S 的尽头。
    本题的思路中，第 2 步相当于在寻找一个「可行解」，然后第 3 步在优化这个「可行解」，最终找到最优解。
    下图流程图；
    1.needs 和 window 相当于计数器，分别记录 T 中字符出现次数和「窗口」中的相应字符的出现次数。
    在这里插入图片描述
    2.增加 right，直到窗口 [left, right) 包含了 T 中所有字符：
    在这里插入图片描述
    3.现在开始增加 left，缩小窗口 [left, right)：
    在这里插入图片描述
    4.直到窗口中的字符串不再符合要求，left 不再继续移动：
    在这里插入图片描述
    5.之后再重复上文过程，直到 right 到达字符串末端。
    首先，初始化代码：
//need 用于记录需要的字符
unordered_map<char, int> need, window;
for (char c : t) need[c]++;

使用 left 和 right 变量初始化窗口的两端，不要忘了，区间 [left, right) 是左闭右开的，所以初始情况下窗口没有包含任何元素：

int left = 0, right = 0;
int valid = 0; 
while (right < s.size()) {
    // 开始滑动
}

其中 valid 变量表示窗口中满足 need 条件的字符个数，如果 valid 和 need.size 的大小相同，则说明窗口已满足条件，已经完全覆盖了串 T。

class Solution {
public:
    string minWindow(string s, string t) {
        unordered_map<char,int>need,window;
        for(char c:t)
        {
            need[c]++;
        }
        int left = 0, right = 0;
        int valid = 0;
        int start = 0;
        int len = INT_MAX;
        while(right < s.size())
        {
            char c = s[right];
            //窗口扩大
            right++;

            if(need.count(c))
            {
                window[c]++;
                if(window[c] == need[c])
                {
                    valid++;
                }
            }

            //判断左边是否需要收缩
            while(valid == need.size())
            {
                if(right - left < len)
                {
                    start = left;
                    len = right-left;
                }

                char d = s[left];
                left++;
                if(need.count(d))
                {
                    if(window[d] == need[d])
                    {
                        valid--;
                    }
                    window[d]--;
                }
            }
        }
        return  len == INT_MAX ? "" : s.substr(start,len);
    }
};

6.3 字符串排列

力扣第 567 题「字符串的排列」
该题：属于和上文一样，直接调用滑动窗口模板

class Solution {
public:
    bool checkInclusion(string s1, string s2) {
        unordered_map<char,int>need,window; 
        int left = 0 ,right = 0;
        int valid = 0;
        for(char c : s1)
        {
            need[c]++;
        }

        while(right<s2.size())
        {
            char c = s2[right];
            right++;
            if(need.count(c))
            {
                window[c]++;
                if(window[c] == need[c])
                {
                    valid++;
                }
            }
            while(right - left >= s1.size())
            {
                if(valid == need.size())
                {
                    return true;
                }
                char d = s2[left];
                left++;
                if(need.count(d))
                {
                    if(window[d] == need[d])
                    {
                        valid--;
                    }
                    window[d]--;
                }
            }
        }
        return false;
    }
};

6.4 最长无重复子串

力扣第 3 题「无重复字符的最长子串」
思路和模板滑动窗口无疑

class Solution {
public:
    int lengthOfLongestSubstring(string s) {
        unordered_map<char,int>window;
        int left = 0;
        int right = 0;
        int res = 0;
        while(right < s.size())
        {
            char c = s[right];
            right++;
            //窗口数据更新
            window[c]++;
            
            //缩小窗口
            while(window[c]>1)
            {
                char d = s[left];
                left++;
                window[d]--;
            }
            res = max(res,right-left);
        }
        return res;
    }
};

6.5 滑动窗口总结

滑动窗口主要就是两个步骤
1：窗口数据更新问题
判断该数据是否需要更新，需要则放入窗口中。

        // 进行窗口内数据的一系列更新
        if (need.count(c)) {
            window[c]++;
            if (window[c] == need[c])
                valid++;
        }

2：窗口是否需要收缩
左右数值差是否达到收缩标准，其中还有关键一步，需要收缩了，你的窗口数据又如何更新

        // 判断左侧窗口是否要收缩
        while (right - left >= t.size()) {
            char d = s[left];
            left++;
            // 进行窗口内数据的一系列更新
            if (need.count(d)) {
                if (window[d] == need[d])
                    valid--;
                window[d]--;
            }
        }

6.6 窗口算法延申：Rabin Karp 字符匹配算法

6.6.1 基础

字符串如何转化为数字

int main() {
    string s = "8264";
    int number = 0;
    for (int i = 0; i < s.size(); i++) {
        // 将字符转化成数字
        number = 10 * number + (s[i] - '0');
        cout << number << endl;
    }
    // 打印输出：
    // 8
    // 82
    // 826
    // 8264
    return 0;
}

这个算法的核心思路就是不断向最低位（个位）添加数字，同时把前面的数字整体左移一位（乘以 10）。
那相反，如何删除最高为数字呢？

/* 在最低位添加一个数字 */
int number = 8264;
// number 的进制
int R = 10;
// 想在 number 的最低位添加的数字
int appendVal = 3;
// 运算，在最低位添加一位
number = R * number + appendVal;
// 此时 number = 82643

/* 在最高位删除一个数字 */
int number = 8264;
// number 的进制
int R = 10;
// number 最高位的数字
int removeVal = 8;
// 此时 number 的位数
int L = 4;
// 运算，删除最高位数字
number = number - removeVal * R^(L-1);
// 此时 number = 264
6.6.2 高效寻找重复子序列

力扣第 187 题「重复的 DNA 序列」
思路一：暴力解法，就挨个遍历，每10个加入到 need 中，然后进行对比，查看是否重复，重复，则加入到 res 中。

class Solution {
public:
    vector<string> findRepeatedDnaSequences(string s) {
        unordered_set<string>need,result;
        int n = s.size();

         for(int i = 0 ;i+10<=n;i++)
         {
             string temp = s.substr(i,10);
             //查看need中是否存在，存在则代表重复
             if(need.count(temp))
             {
                 result.insert(temp);
             }
             //不存在，则加入到need中
             else
             {
                 need.insert(temp);
             }
         }
         //此处需要返回 vector<string> 是因为函数返回值，不能直接返回result
         return vector<string>(result.begin(),result.end()) ;
    }
};

思路二：本章节主要介绍的滑动窗口问题

class Solution {
public:
    vector<string> findRepeatedDnaSequences(string s) {
    // 先把字符串转化成四进制的数字数组
    vector<int> nums(s.length());
    for (int i = 0; i < nums.size(); i++) {
        switch (s[i]) {
            case 'A':
                nums[i] = 0;
                break;
            case 'G':
                nums[i] = 1;
                break;
            case 'C':
                nums[i] = 2;
                break;
            case 'T':
                nums[i] = 3;
                break;
        }
    }
    // 记录重复出现的哈希值
    unordered_set<int> seen;
    // 记录重复出现的字符串结果
    unordered_set<string> res;

    // 数字位数
    int L = 10;
    // 进制
    int R = 4;
    // 存储 R^(L - 1) 的结果
    int RL = pow(R, L - 1);
    // 维护滑动窗口中字符串的哈希值
    int windowHash = 0;

    // 滑动窗口代码框架，时间 O(N)
    int left = 0, right = 0;
    while (right < nums.size()) {
        // 扩大窗口，移入字符，并维护窗口哈希值（在最低位添加数字）
        windowHash = R * windowHash + nums[right];
        right++;

        // 当子串的长度达到要求
        if (right - left == L) {
            // 根据哈希值判断是否曾经出现过相同的子串
            if (seen.count(windowHash)) {
                // 当前窗口中的子串是重复出现的
                res.insert(s.substr(left, right - left));
            } else {
                // 当前窗口中的子串之前没有出现过，记下来
                seen.insert(windowHash);
            }
            // 缩小窗口，移出字符，并维护窗口哈希值（删除最高位数字）
            windowHash = windowHash - nums[left] * RL;
            left++;
        }
    }
    // 转化成题目要求的 vector 类型
    return vector<string>(res.begin(), res.end());
    }
};
6.6.3 算法逻辑总结、模板

通过子串和模式串的比较得到最终结果，滑动窗口巧妙：运用滑动哈希算法一边滑动一边计算窗口中字符串的哈希值，拿这个哈希值去和模式串的哈希值比较，这样就可以避免截取子串，从而把匹配算法降低为 O(N)

#include <string>
#include <cmath>

using namespace std;

int numDistinct(string s, string t) {
    // 文本串
    string txt = s;
    // 模式串
    string pat = t;

    // 需要寻找的子串长度为模式串 pat 的长度
    int L = pat.length();
    // 仅处理 ASCII 码字符串，可以理解为 256 进制的数字
    int R = 256;
    // 存储 R^(L - 1) 的结果
    int RL = pow(R, L - 1);
    // 维护滑动窗口中字符串的哈希值
    int windowHash = 0;
    // 计算模式串的哈希值
    long long patHash = 0;
    for (int i = 0; i < pat.length(); i++) {
        patHash = R * patHash + pat[i];
    }

    // 滑动窗口代码框架
    int left = 0, right = 0;
    while (right < txt.length()) {
        // 扩大窗口，移入字符（在最低位添加数字）
        windowHash = R * windowHash + txt[right];
        right++;

        // 当子串的长度达到要求
        if (right - left == L) {
            // 根据哈希值判断窗口中的子串是否匹配模式串 pat
            if (patHash == windowHash) {
                // 找到模式串
                printf("找到模式串，起始索引为 %d", left);
                return left;
            }

            // 缩小窗口，移出字符（删除最高位数字）
            windowHash = windowHash - txt[left] * RL;
            left++;
        }
    }
    // 没有找到模式串
    return -1;
}

改模板存在问题，就是整型溢出问题，所以可以取模：


#include <string>
#include <cmath>

using namespace std;

// Rabin-Karp 指纹字符串查找算法
int rabinKarp(string txt, string pat) {
    // 位数
    int L = pat.length();
    // 进制（只考虑 ASCII 编码）
    int R = 256;
    // 取一个比较大的素数作为求模的除数
    long Q = 1658598167;
    // R^(L - 1) 的结果
    long RL = 1;
    for (int i = 1; i <= L - 1; i++) {
        // 计算过程中不断求模，避免溢出
        RL = (RL * R) % Q;
    }
    // 计算模式串的哈希值，时间 O(L)
    long patHash = 0;
    for (int i = 0; i < pat.length(); i++) {
        patHash = (R * patHash + pat.at(i)) % Q;
    }

    // 滑动窗口中子字符串的哈希值
    long windowHash = 0;

    // 滑动窗口代码框架，时间 O(N)
    int left = 0, right = 0;
    while (right < txt.length()) {
        // 扩大窗口，移入字符
        windowHash = ((R * windowHash) % Q + txt.at(right)) % Q;
        right++;

        // 当子串的长度达到要求
        if (right - left == L) {
            // 根据哈希值判断是否匹配模式串
            if (windowHash == patHash) {
                // 当前窗口中的子串哈希值等于模式串的哈希值
                // 还需进一步确认窗口子串是否真的和模式串相同，避免哈希冲突
                if (pat.compare(txt.substr(left, L)) == 0) {
                    return left;
                }
            }
            // 缩小窗口，移出字符
            windowHash = (windowHash - (txt.at(left) * RL) % Q + Q) % Q;
            // X % Q == (X + Q) % Q 是一个模运算法则
            // 因为 windowHash - (txt[left] * RL) % Q 可能是负数
            // 所以额外再加一个 Q，保证 windowHash 不会是负数

            left++;
        }
    }
    // 没有找到模式串
    return -1;
}

七：二分搜索

7.1 二分查找框架

二分查找思路：每次查找都从中间往两边进行查询

int binarySearch(vector<int>& nums, int target) {
    int left = 0, right = nums.size() - 1;

    while(left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            ...
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        }
    }
    return ...;
}

二分查找注意事项：不要出现 else，而是把所有情况用 else if 写清楚，这样可以清楚地展现所有细节

 mid = left + (right - left) / 2;
 mid = (left + right) / 2

这两行结果都是一样的，但是第一行可以防止溢出问题。

7.2 寻找一个数（最基本二分搜索）

力扣第 704 题「二分查找」

class Solution {
public:
    int search(vector<int>& nums, int target) {
        int left = 0;
        int right = nums.size() - 1;
        while(left<=right)
        {
            int mid = left + (right - left) / 2 ;
            if(nums[mid] == target)
            {
                return mid;
            }
            else if(nums[mid] > target)
            {
                right = mid - 1;
            }
            else if(nums[mid] < target)
            {
                left = mid + 1;
            }
        }
        return -1;
    }
};

存在一个问题：比如说给你有序数组 nums = [1,2,2,2,3]，target 为 2，此算法返回的索引是 2，没错。但是如果我想得到 target 的左侧边界，即索引 1，或者我想得到 target 的右侧边界，即索引 3，这样的话此算法是无法处理的。
while 循环中 <= 与 < 有什么区别？ 区别是：前者相当于两端都闭区间 [left, right]，后者相当于左闭右开区间 [left, right)。

7.3 左侧边界二分搜索问题

左侧边界，左闭右开

int left_bound(vector<int>& nums, int target) {
    int left = 0;
    int right = nums.size(); // 注意
    
    while (left < right) { // 注意
        int mid = left + (right - left) / 2;
        if (nums[mid] == target) {
            right = mid;
        } else if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid; // 注意
        }
    }
    return left;
}

while(left < right) 终止的条件是 left == right，此时搜索区间 [left, left) 为空，所以可以正确终止。
这个时候会存在一个问题，倘若整个数组找不到需要的东西，属于索引越界了，怎么办？

while (left < right) {
    //...
}
// 如果索引越界，说明数组中无目标元素，返回 -1
if (left < 0 || left >= nums.length) {
    return -1;
}
// 判断一下 nums[left] 是不是 target
return nums[left] == target ? left : -1;

为了避免左右是否闭合问题，下文代码给出同一的左右闭合代码；

int left_bound(vector<int>& nums, int target) {
    int left = 0, right = nums.size() - 1;
    // 搜索区间为 [left, right]
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            // 搜索区间变为 [mid+1, right]
            left = mid + 1;
        } else if (nums[mid] > target) {
            // 搜索区间变为 [left, mid-1]
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 收缩右侧边界
            right = mid - 1;
        }
    }
    // 判断 target 是否存在于 nums 中
    // 如果越界，target 肯定不存在，返回 -1
    if (left < 0 || left >= nums.size()) {
        return -1;
    }
    // 判断一下 nums[left] 是不是 target
    return nums[left] == target ? left : -1;
}

7.4 右侧边界二分搜索问题

7.5 总结

1.下面是左右双闭的写法，分别为基础二分搜索、左侧搜索、右侧搜索：

int binary_search(vector<int>& nums, int target) {
    int left = 0, right = nums.size()-1; 
    while(left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1; 
        } else if(nums[mid] == target) {
            // 直接返回
            return mid;
        }
    }
    // 直接返回
    return -1;
}

int left_bound(vector<int>& nums, int target) {
    int left = 0, right = nums.size()-1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 别返回，锁定左侧边界
            right = mid - 1;
        }
    }
    // 判断 target 是否存在于 nums 中
    if (left < 0 || left >= nums.size()) {
        return -1;
    }
    // 判断一下 nums[left] 是不是 target
    return nums[left] == target ? left : -1;
}

int right_bound(vector<int>& nums, int target) {
    int left = 0, right = nums.size()-1;
    while (left <= right) {
        int mid = left + (right - left) / 2;
        if (nums[mid] < target) {
            left = mid + 1;
        } else if (nums[mid] > target) {
            right = mid - 1;
        } else if (nums[mid] == target) {
            // 别返回，锁定右侧边界
            left = mid + 1;
        }
    }
    // 判断 target 是否存在于 nums 中
    // if (left - 1 < 0 || left - 1 >= nums.size()) {
    //     return -1;
    // }
    
    // 由于 while 的结束条件是 right == left - 1，且现在在求右边界
    // 所以用 right 替代 left - 1 更好记
    if (right < 0 || right >= nums.size()) {
        return -1;
    }
    return nums[right] == target ? right : -1;
}

八：带权重的随机选择法

8.1 基础

CC爆
关注
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值