AcWing 2014. 岛附图解超详细过程

最新推荐文章于 2025-08-14 22:07:01 发布

原创最新推荐文章于 2025-08-14 22:07:01 发布 · 877 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#算法 #usaco #java #c++ #枚举类

Java 同时被 3 个专栏收录

22 篇文章

订阅专栏

C/C++

18 篇文章

订阅专栏

AcWing

17 篇文章

订阅专栏

本文针对一场暴雨导致农田被洪水淹没的问题，详细分析了如何计算最大岛屿数量的变化过程。通过模拟洪水上升淹没不同高度的田地，探讨了各种情况下岛屿数量的变化规律。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

题目

每当下雨时，农夫约翰的田地总是被洪水淹没。

由于田地不是完全水平的，所以一些地方充满水后，留下了许多被水隔开的“岛”。

约翰的田地被描述为由 N 个连续高度值 H1,…,HN 指定的一维场景。

假设该场景被无限高的围墙包围着，请考虑暴雨期间发生的情况：

最低处首先被水覆盖，形成一些不连贯的岛，随着水位的不断上升，这些岛最终都会被覆盖。

一旦水位等于一块田地的高度，那块田地就被认为位于水下。

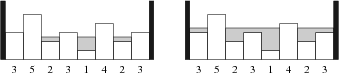
在这里插入图片描述

上图显示了一个示例：在左图中，我们只加入了刚好超过 1 单位的水，此时剩下 4 个岛（最大岛屿剩余数量），而在右图中，我们共加入了 7 单位的水，此时仅剩下 2 个岛。

请计算，暴风雨期间我们能在某个时间点看到的最大岛屿数量。

水会一直上升到所有田地都在水下。

输入格式
第一行包含整数 N。

接下来 N 行，每行包含一个整数表示 Hi。

输出格式
输出暴风雨期间我们能在某个时间点看到的最大岛屿数量。

数据范围
1 ≤ N ≤ 10⁵,
1 ≤ H_i ≤ 10⁹

输入样例：

输出样例：

分析过程

理解样例

首先，我们先来理解一下题意

样例示意1
在左图中：
蓝色线的高度为 1 ，蓝色部分是一单位水，而蓝色线上方的水就是原题中说的超过一单位的部分，可见高度为 1 和 2 的田已经被淹没了。
此时， 3 和 5 在水面上且连在一起，是一个岛；
中间高度为 3 的田还在水面上，是一个孤岛
4 还在水面上，是一个孤岛
右侧高度为 3 的田也还在水面上，也是一个孤岛
共有四个岛；

在右图中：
红色线的高度为 1，红色部分是一单位水；
蓝色线的高度为 3，蓝色部分是三单位水；
蓝线上方的水是平分三单位水，这就构成了题中的 7 单位水；
此时，5 还在水面上，是一个孤岛；
4 也还在水面上，也是一个孤岛；
共有两个岛；

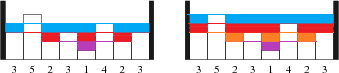
样例示意2
在左图中：
液面高度为 4，即加入了 [10,17) 单位的水；
此时，只有高度为 5 的田还在水面上，是一个孤岛；
共有一个岛；

在右图中：
页面高度为 5，即加入了 [17,∞) 单位的水；
此时，没有一块田地在水面上，
共有 0 个岛。

所以，在淹没过程中我们能看到的最大岛屿为 4 个。

解题思路

由对样例的分析可以看出，田是否被淹没，我们只需要关心他的高度是否大于等于田的高度（题中说一旦水位等于一块田地的高度，那块田地就被认为位于水下；即使题中未说明，我们也可以通过添加一点点水来淹没它）。

所以，我们可以通过模拟淹没的方法来解这道题。

而模拟的次数等于田不同高度的数量，因为高度相同的田会在同一时间被淹没。

例如样例中先后灌入高度为 1，2，3，4，5 的水，直至全部被淹没。

而在淹没的过程中，我们会遇到如下几种情况：
1.田不在最左端，也不在最右端，且中间的田比相邻两侧的高，即孤岛，如下图：

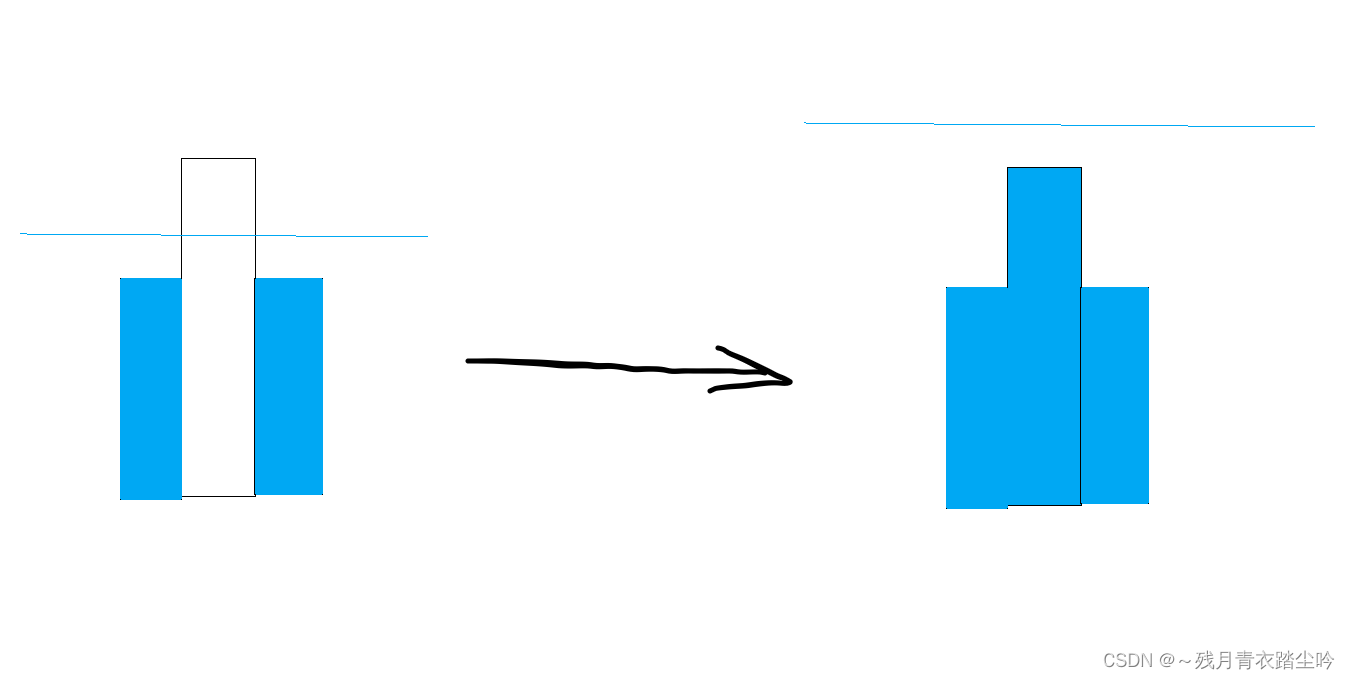
中间高，两边低

如果此时该田被淹没，那么岛屿的数量就会减 1；

2.田不在最左端，也不在最右端，且中间的田比相邻两侧的矮，即洼地，如下图：

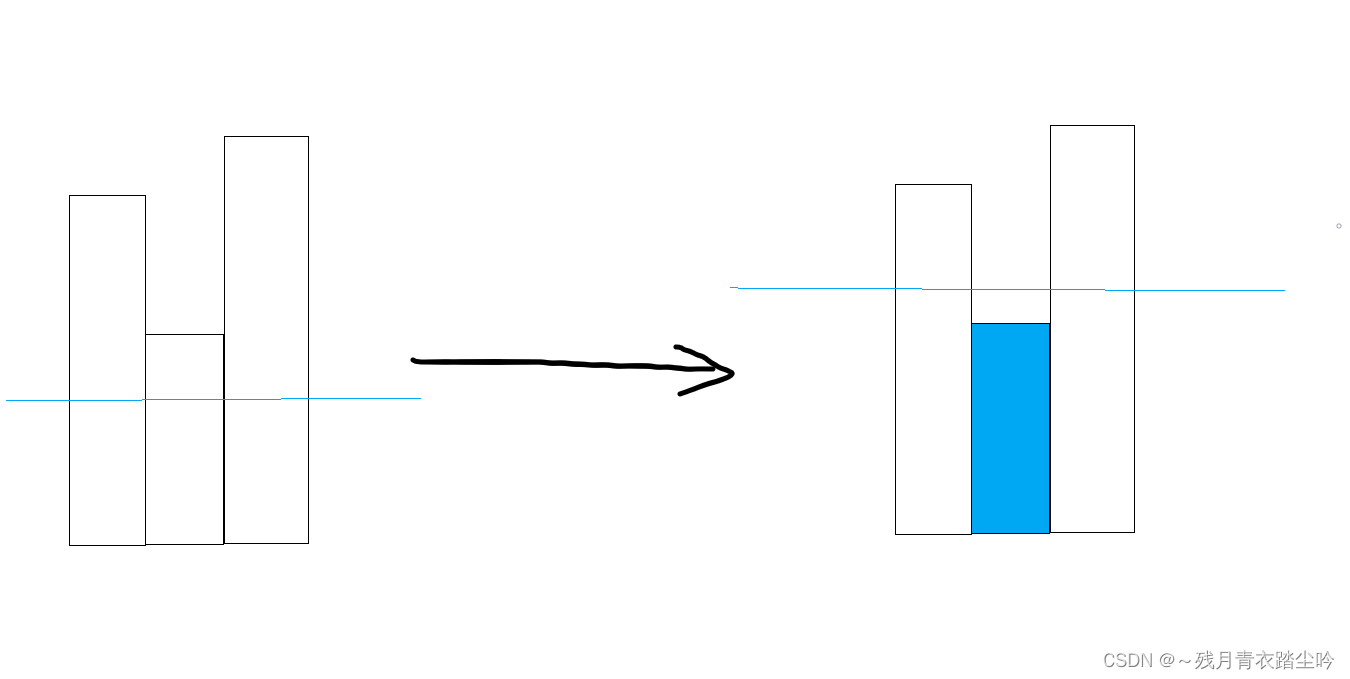
中间低，两边高

如果此时该田被淹没，那么左右两边高于它的田，会形成两个岛，而之前这三块田连在一起只有一个岛屿，说明岛屿的数量会加 1；

3.在岛屿的最左端，且其右边的田比其矮，即孤岛，如下图：
如果该田此时被淹没，这座孤岛就会消失，说明岛屿的数量会减 1；

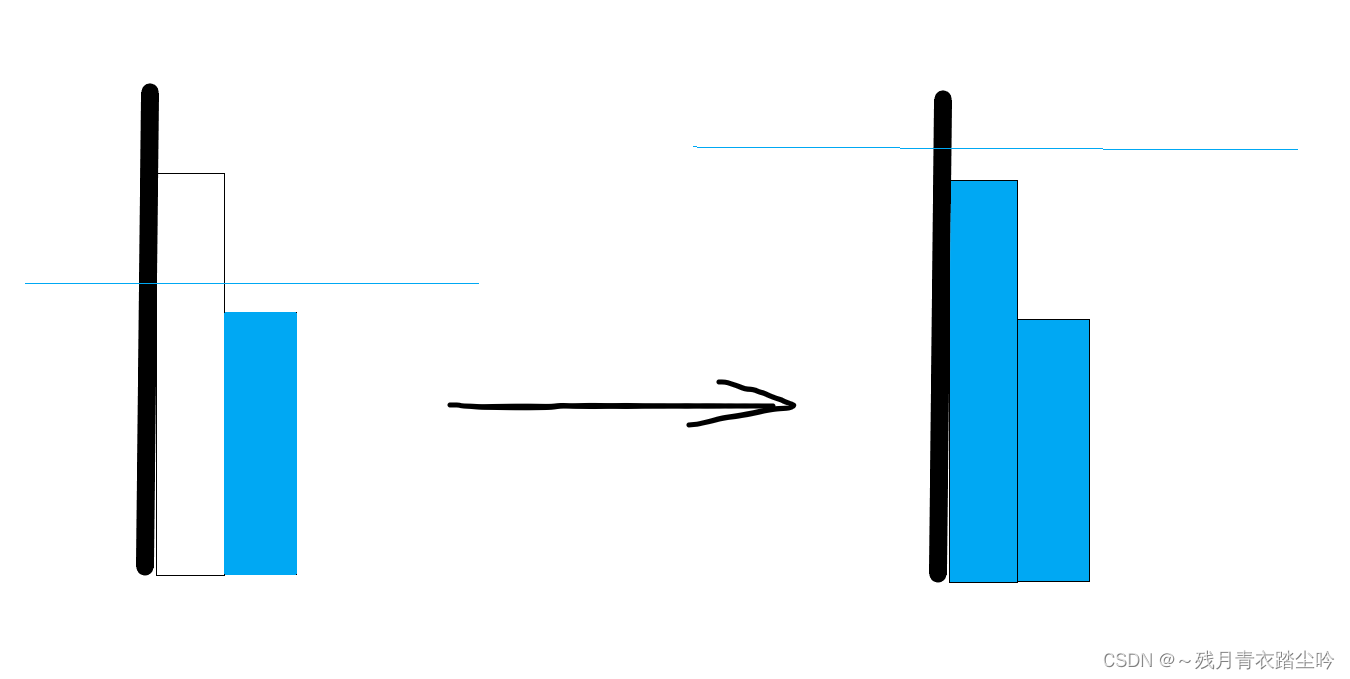
岛屿的最左端，且其右边的田比其矮

4.在岛屿的最右端，且其左边的田比其矮，即孤岛，如下图：
如果该田此时被淹没，这座孤岛就会消失，说明岛屿的数量会减 1；

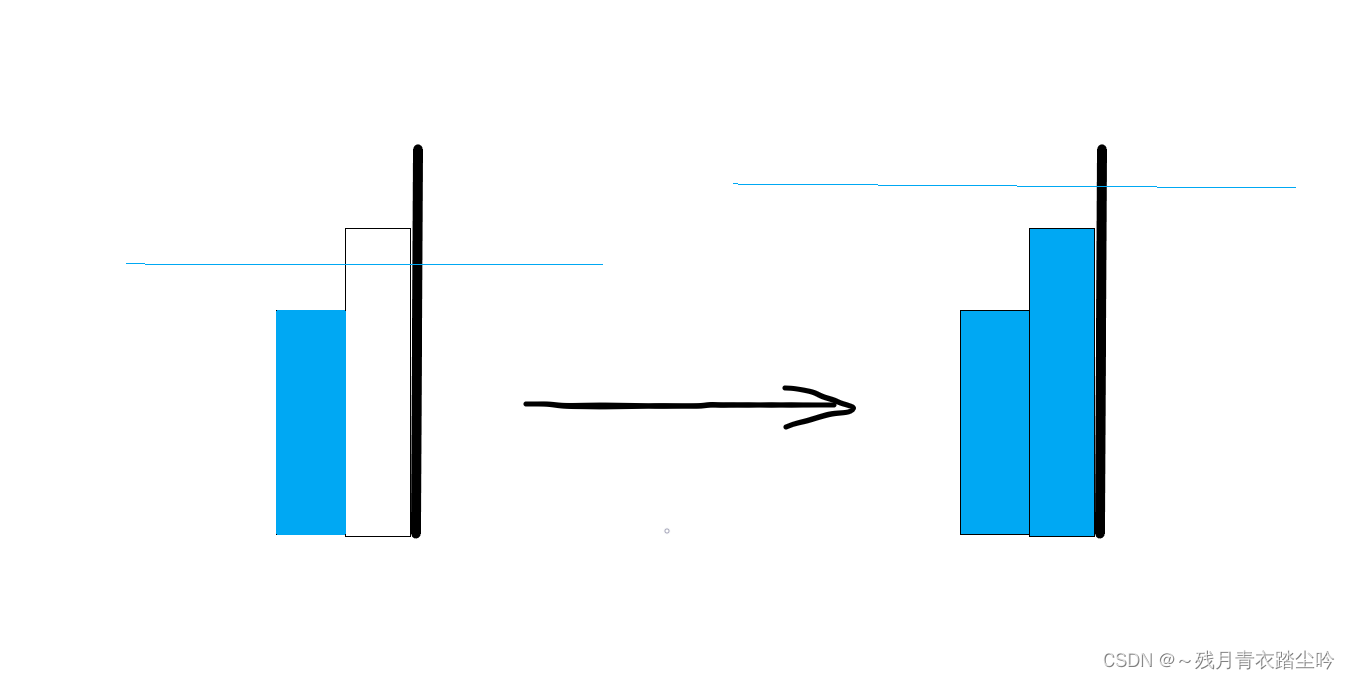
在这里插入图片描述

5.不在最左端，也不在最右端，中间的田比一侧高，比一侧矮，则淹没它对岛屿数量没有贡献，并不会增加或者减少岛屿数量，如下图：

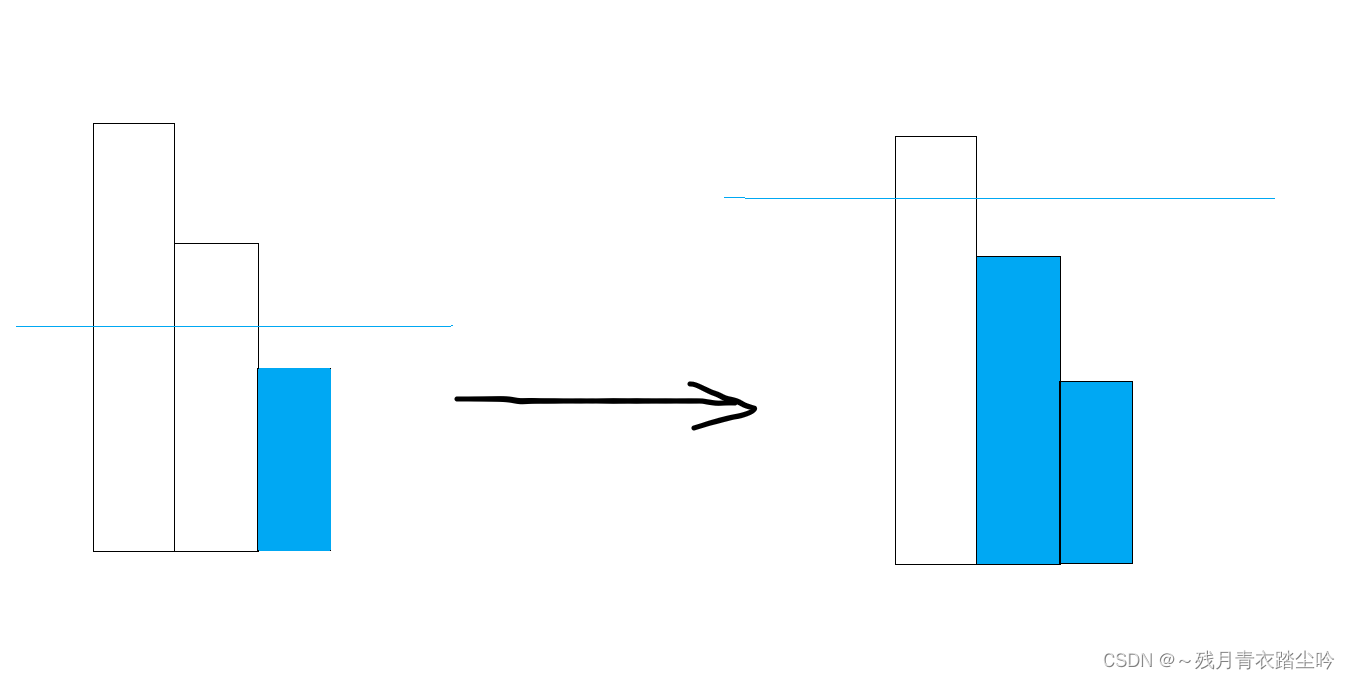
不在最左端，也不在最右端，中间的田比右侧高，比左侧矮

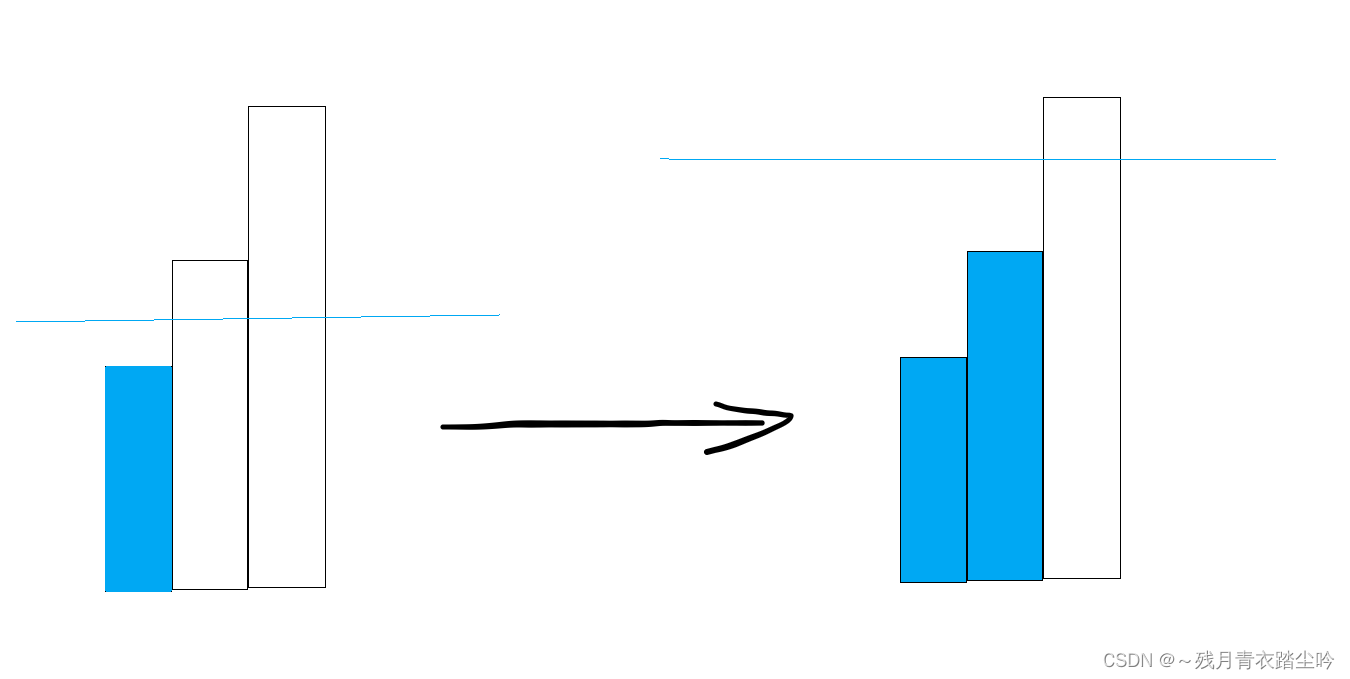
不在最左端，也不在最右端，中间的田比左侧高，比右侧矮

6.在岛屿的最左端，且其右边的田比其高，如下图：

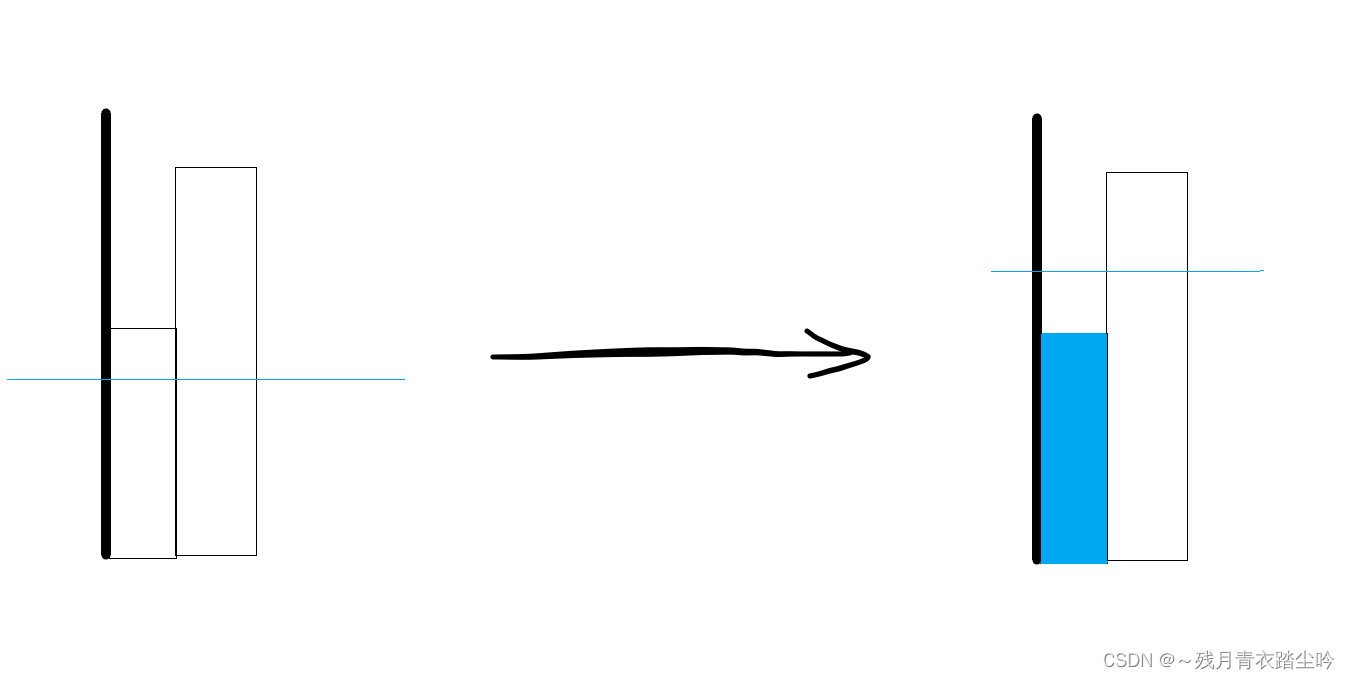
在岛屿的最左端，且其右边的田比其高

则该田被淹没没有影响；

7.在岛屿的最右端，且其左边的田比其高，如下图：

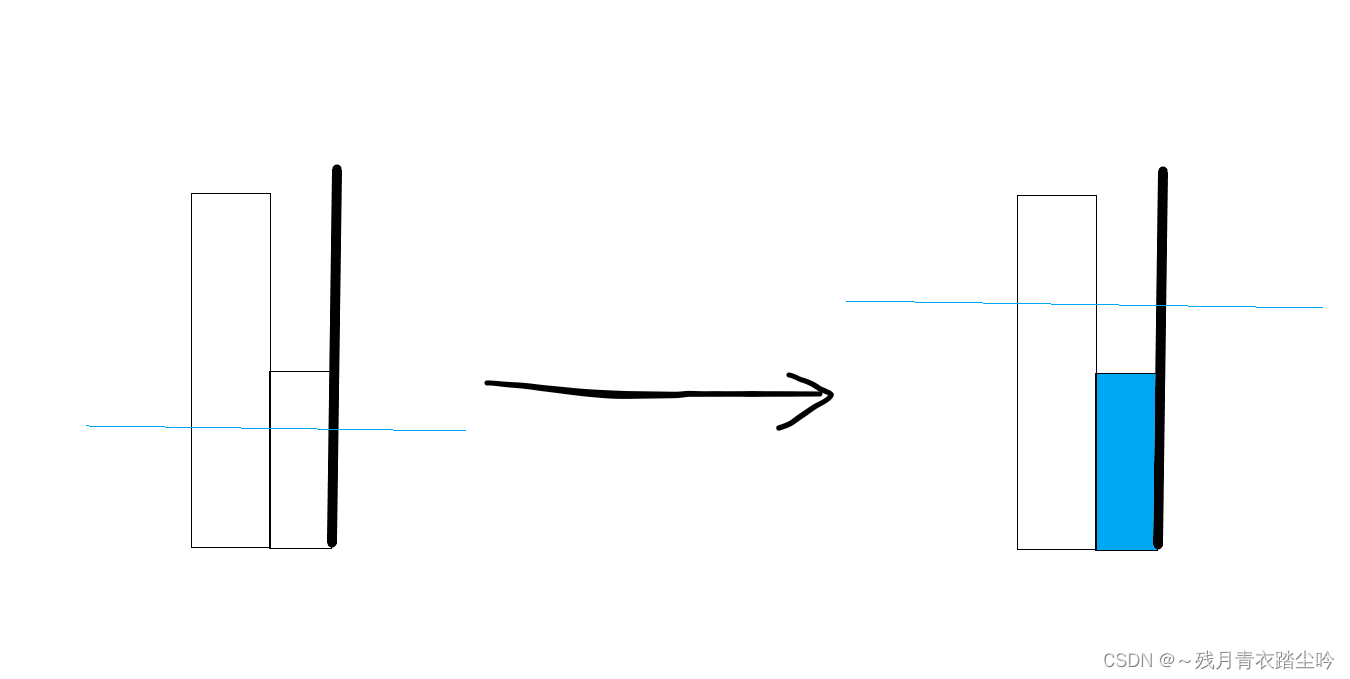
在岛屿的最右端，且其左边的田比其高

则该田被淹没没有影响；

8.与之相连的田与之高度相同，由于会同时被淹没，所以这些相连的、高度相同的田可以看作是同一块田，在读入的时候可以直接将相连的且高度相同的田合并（合并的充分性），如下图：

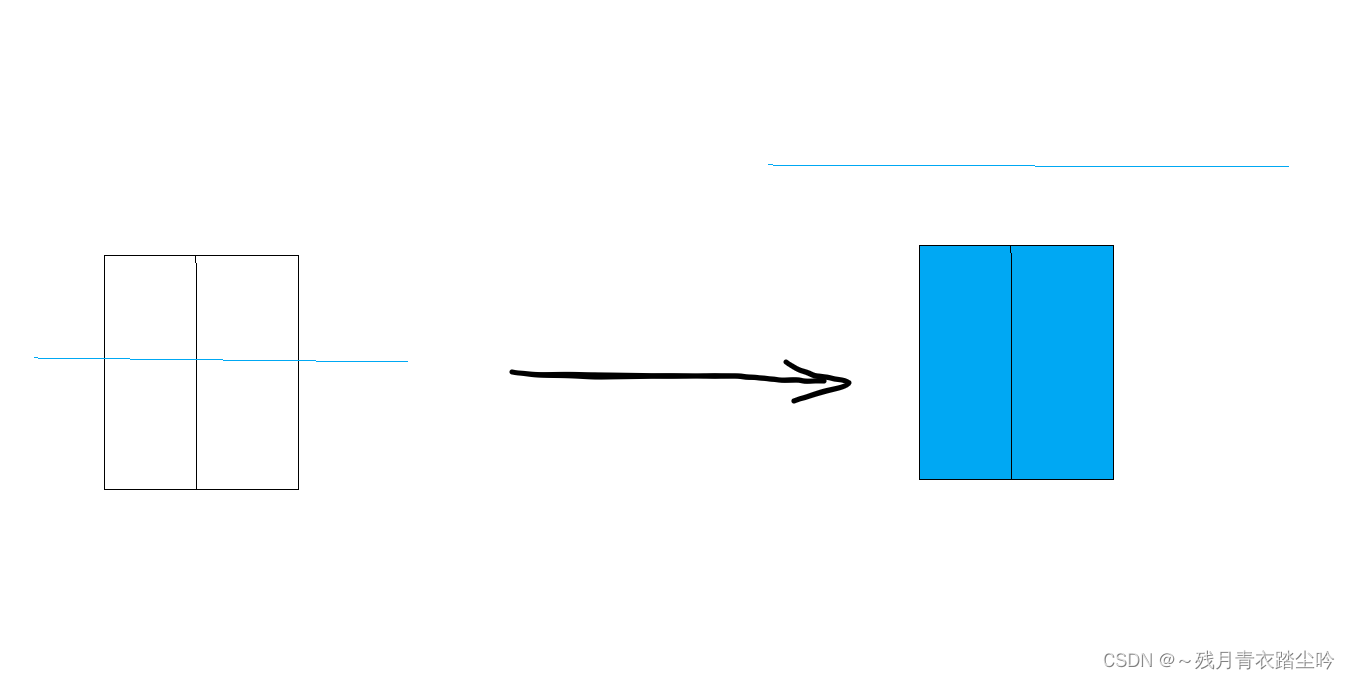
相邻的高度想同的田去重的充分性证明

如果我们在淹没两个相连的高度相同的岛时，但看其中一个我们无法判断淹没它对岛屿的贡献，即无法明确知道淹没该田后岛屿数是增加，减少，还是不变，如下图：（合并的必要性）

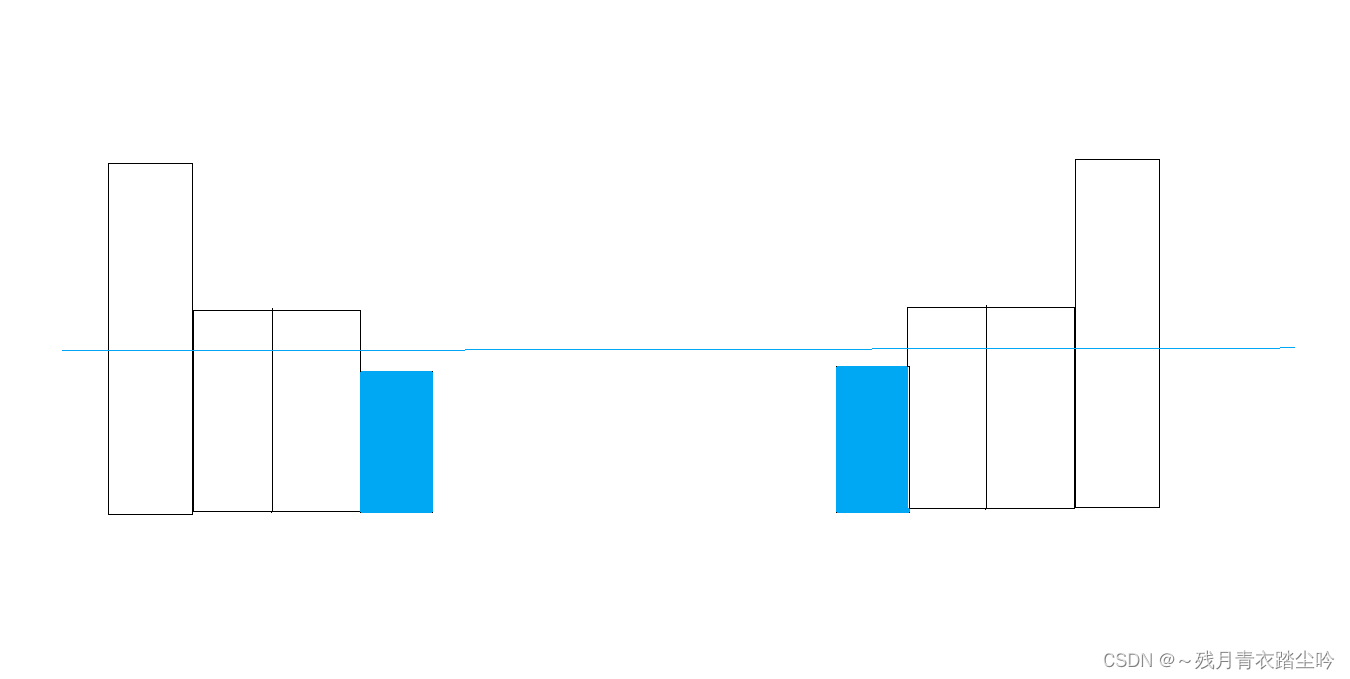
中间相同，左高右低或左低右高

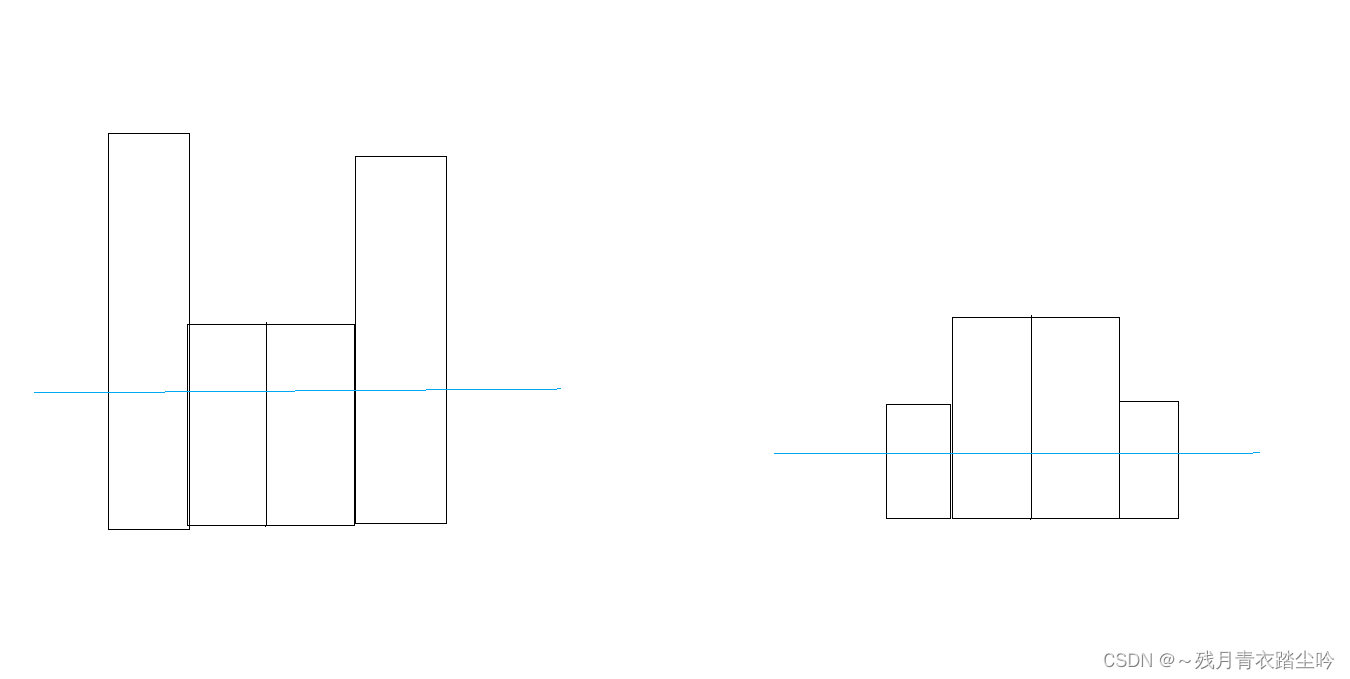
中间相同，两边高或两边低

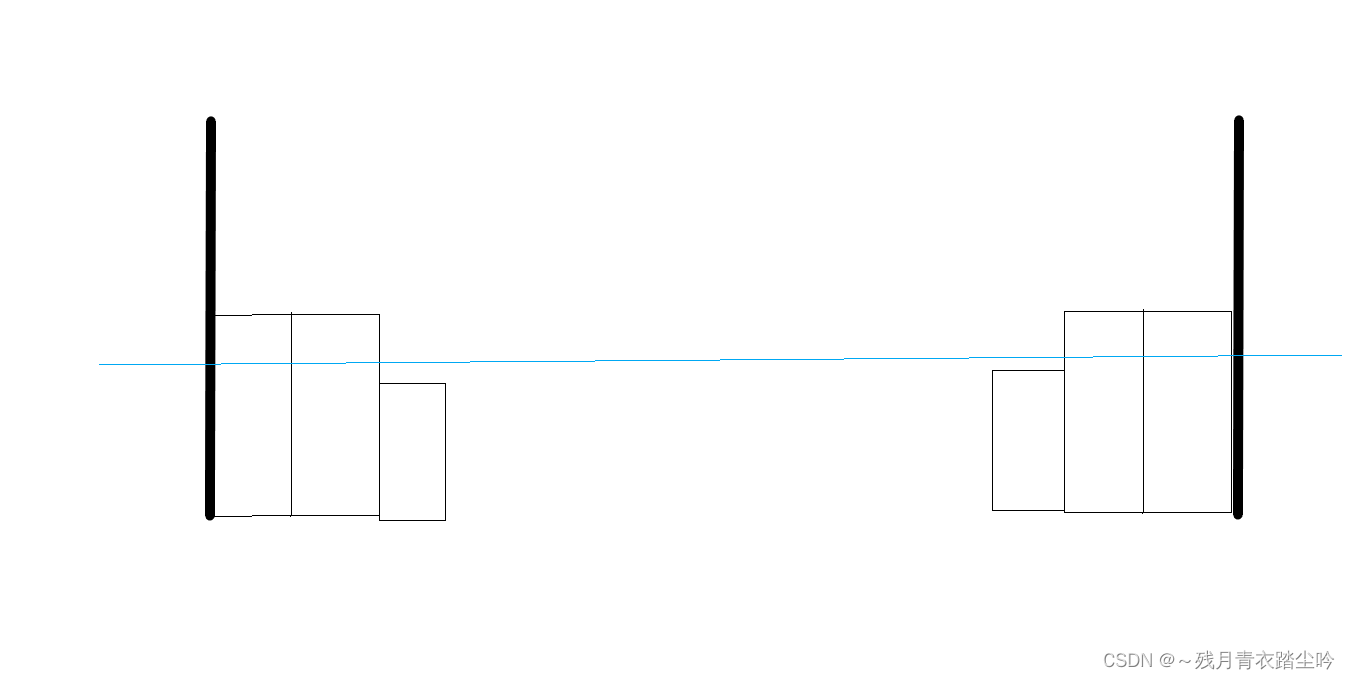
在两端，且比边上的高
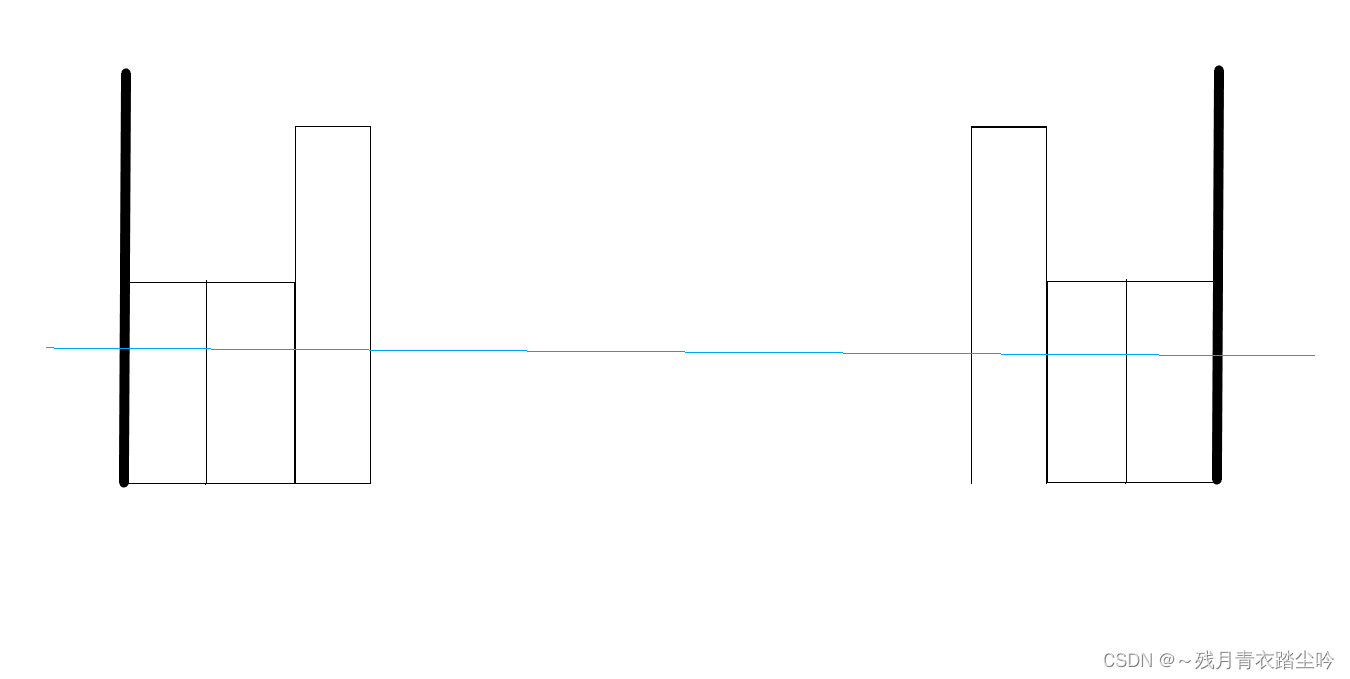
在两端，且比边上矮
从上面这些图可以看出，当两块相同高度的田连在一起时，无法通过一块田判断淹没该田对总岛数的贡献。

所以，读入数据时我们先对相邻的高度相同的田进行去重。

然后将田由低到高进行升序排序，并由低到高模拟被淹没的情形。

注意：由于同一高度是在同一时间被淹没的，所以更新岛的数量的时候，需要等相同高度的所有岛都淹没完才能更新。

AC代码

C++

#include <iostream>
#include <cstring>
#include <algorithm>

#define x first
#define y second

using namespace std;

typedef pair<int, int> PII;

const int N = 100001;

int n;
int h[N];   // 记录田的高度
PII q[N];   // 记录该高度的田的原始位置

int main()
{
    scanf("%d", &n);

    for(int i = 0; i < n; i++) scanf("%d", &h[i]);

    n = unique(h, h + n) - h;   // 将相邻的高度相同的田去重

    for(int i = 0; i < n; i++) q[i] = {h[i], i};    // 记录田原始的相对位置

    sort(q, q + n); // 将田升序排序，方便从低到高模拟淹没

    int current = 1;    // 记录当前的岛屿数量，最开始所有田都是同一个岛屿
    int res = 1;    // 记录最大的岛屿数量
    int pre = -1;   // 记录前一块淹没的田的数量
    for(int i = 0; i < n; i++)
    {
        int high = q[i].x;  // 当年淹没的高度
        int j = q[i].y; // 当前淹没的田的原始位置

        if(high != pre) // 如果前一个高度的田已经全部淹没完了，则更新当前的岛屿数
        {
            pre = high; // 表示开始淹没新的高度的田了
            res = max(res, current);
        }

        if(j - 1 >= 0 && j + 1 < n)
        {
            if(high > h[j - 1] && high > h[j + 1]) current--;   // 如果中间的田比两侧的高，即孤岛
            else if(high < h[j - 1] && high < h[j + 1]) current++;  // 如果中间的田比两侧的低，即洼地
        }

        if(j == 0 && h[j] > h[j + 1]) current--;
        else if(j + 1 == n && h[j] > h[j - 1]) current--;
    }

    res = max(res, current);
    printf("%d\n", res);
}

Java

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.io.PrintWriter;
import java.util.Arrays;

public class Main {
	
	public static void main(String[] args) throws IOException {
		BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
		PrintWriter out = new PrintWriter(System.out);
		
		int n = Integer.parseInt(in.readLine());	// N 个连续的高度值
		int[] height = new int[n];	// n 个高度
		int max = 1;	// 最多的岛屿数，没有田被淹没时可以看作是一整个岛
		int current = 1;	// 淹没当前岛屿后的岛屿数，没有田被淹没时可以看作是一整个岛
		int pre = -1;	// 前一个输入的值
		
		for(int i = 0; i < n; i++) {
			int h = Integer.parseInt(in.readLine());
			if(h == pre) {	// 如果当前输入和前一个相同，说明两个高度相同，则忽略当前高度，与前一块田合并
				n--;
				i--;
			}
			else {
				height[i] = h;
				pre = h;
			}
		}
		
		Island[] islands = new Island[n];
		for(int i = 0; i < n; i++) {
			islands[i] = new Island(i, height[i]);
		}
		
		Arrays.sort(islands);	// 将田按高度升序
		
		pre = -1;	// 当前淹没的田的高度
		for(Island island : islands) {
			int self = island.i;	// 当前田的位置
			int left = self - 1;	// 当前田的左侧
			int right = self + 1;	// 当前田的右侧
			int h = island.h;	// 当前田的高度
			
			if(h != pre) {
				max = Math.max(max, current);	// 如果当前田的高度与上一个不同，则说明上一个高度的田已经被淹完了，则更新当前最大岛屿数
				pre = h;
			}
			
			// 当左右两侧均有岛屿时
			if(left >= 0 && right < n) {
				// 当左右两侧的田都比该田高时，则该田被淹没后会将原来的一个岛屿划分出两个岛屿
				if(height[left] > h && height[right] > h) current++;
				
				// 当左右两侧的田都比该田矮时，则说明该田已经是孤岛，被淹没后岛屿数减一
				if(height[left] < h && height[right] < h) current--;
			}
			
			// 当该田在最左侧时，且该田右边的田比它矮，说明它也已经是孤岛了，被淹没后岛屿数减一
			// 若该田右侧的田比它高，则对岛屿数没有影响
			if(left < 0 && height[right] < h) current--;
			
			// 当该田在最右侧时，且该田左边的田比它矮，说明它也已经是孤岛了，被淹没后岛屿数减一
			// 若该田左侧的田比它高，则对岛屿数没有影响
			if(right >= n && height[left] < h) current--;
			
		}
		max = Math.max(max, current);
		out.print(max);
		out.flush();
	}
	
	public static class Island implements Comparable<Island> {
		public int i;	// 田的位置
		public int h;	// 田的高度
		
		public Island() {
			this.i = 0;
			this.h = 0;
		}
		
		public Island(int i, int h) {
			this.i = i;
			this.h = h;
		}
		
		@Override
		public int compareTo(Island o) {
			return this.h - o.h;	// 按田高度的升序排序
		}
		
	}

}